---

Toeplitz Matrix

• Toeplitz Matrix 는 주로 Digital Image Processing, Signal Processing, Cryptography 등에 사용된다.
• complex toeplitz 형태도 가능하다.
• 위 사진을 보면 알겠지만, 대각행렬들이 모두 같고 c (column),r (row) 모두 순환되는 구조이다.
• linalg.solve_toeplitz 를 사용하여 해를 구할 수 있다.
• 사용되는 알고리즘은 Levinson-Durbin recursion 이고 $\sim n^2$ 정도의 work-load 가 소요된다.

x = linalg.solve_toeplitz( (c, r), b )

• 예시로, $T = \begin{bmatrix} 1 & -1 & -2 & -3 \\ 3 & 1 & -1 & -2 \\ 6 & 3 & 1 & -1 \\ 10 & 6 & 3 & 1 \end{bmatrix}$ , $\mathbf{b} = \begin{bmatrix} 1 \\ 1 \\ 1 \\ 1 \end{bmatrix}$ 를 풀어보자.

c = np.array([1,3,6,10], dtype=np.float64)

r = np.array([1,-1,-2,-3], dtype=np.float64)

b = np.ones((4,),dtype=np.float64)

x = linalg.solve_toeplitz((c,r),b)

# (c,r) 을 linalg.toeplitz 로 재구축 하려면 비효율적이므로
# 강의에서 제공하는 커스텀 함수를 사용했음
# Ax = b 를 검증
bp = matmul_toeplitz( (c,r), x)

print(bp)

print(np.allclose(bp, b))

print(x)

[1. 1. 1. 1.]
True
[ 1.66666667e-01 -5.27355937e-16 -1.66666667e-01 -1.66666667e-01]

• Toeplitz Matrix 를 구축하는 함수
• linalg.toeplitz
• 거의 쓸일이 없다.

t_full = linalg.toeplitz(c,r)

• 예시 코드

t_full = linalg.toeplitz(c,r)

print(t_full)

[[ 1. -1. -2. -3.]
 [ 3.  1. -1. -2.]
 [ 6.  3.  1. -1.]
 [10.  6.  3.  1.]]

Circulant Matrix

• Ciruclant Matrix 는 한 개의 column이 순환하는 순환 구조임을 알 수 있다.
• linalg.solve_circulant 를 통해 해를 구할 수 있다.

x = linalg.solve_circulant(c,b)

• discrete Fourier transform 을 사용한다.
• fast Fourier transform 은 $\sim n \log n$ -> 엄청 빠름

• 2,-1,0,1,0,0,1 column 이 순환하는 circulant matrix 를 solver 로 풀어보면
• 예시 코드

c = np.array([2,-1,0,1,0,0,1], dtype=np.float64)

b = np.ones((7,) ,dtype=np.float64)

x = linalg.solve_circulant( c, b )

bp = matmul_circulant(c, x)

print(bp)

print(np.allclose(bp, b))

print(x)

[1. 1. 1. 1. 1. 1. 1.]
True
[0.33333333 0.33333333 0.33333333 0.33333333 0.33333333 0.33333333
 0.33333333]

• circulant matrix 구축하는 함수
• linalg.circulant

c_full = linalg.circulant(c)

print(c_full)

[[ 2.  1.  0.  0.  1.  0. -1.]
 [-1.  2.  1.  0.  0.  1.  0.]
 [ 0. -1.  2.  1.  0.  0.  1.]
 [ 1.  0. -1.  2.  1.  0.  0.]
 [ 0.  1.  0. -1.  2.  1.  0.]
 [ 0.  0.  1.  0. -1.  2.  1.]
 [ 1.  0.  0.  1.  0. -1.  2.]]

• 참고사항
• solve_toeplitz 로 circulant matrix 를 풀 수도 있다.
• 왜냐하면 circulant 자체가 toeplitz 의 특수한 케이스이기 때문
• 행렬의 크기가 50000 쯤 가면 solve_circulant 와 solve_toeplitz 연산하는 시간에 엄청난 차이가 발생한다.

• 일반 solve, solve_circulant, solve_toeplitz 계산 속도 비교표

행렬 사이즈 ($n$)	solve_circulant	solve_toeplitz	일반 solve
1000	0.001979	0.0121	0.017
2500	0.002754	0.0237	0.150
5000	0.003199	0.0594	0.745
10000	0.003471	0.2091	4.16
20000	0.004392	0.8017	23.76
50000	0.005860	4.9556	313.38

동시에 여러 행렬방정식 한꺼번에 풀기

• 우리가 배운 행렬 방정식을 푸는 함수들은 $A\mathbf{x} = \mathbf{b}$ 만이 아니라 $AX = B$ 형태도 풀 수 있다.
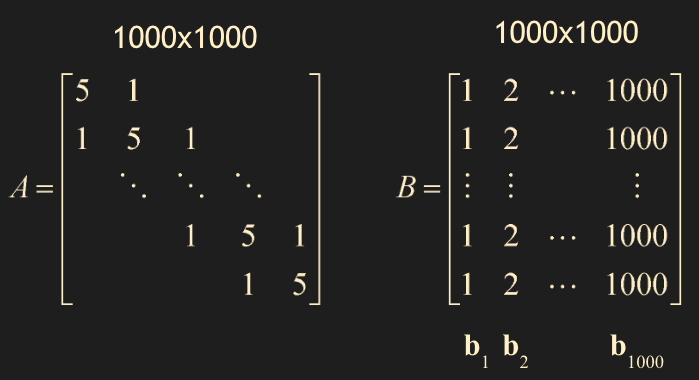
• $AX = B$ 를 푼다는 것은, $ A\mathbf{x}_1 = \mathbf{b}_1 \quad A\mathbf{x}_2 = \mathbf{b}_2 \quad \dots \quad A\mathbf{x}_k = \mathbf{b}_k $ 를 푼다는 것이고
• 여기서 $B = [\mathbf{b}_1 \; \mathbf{b}_2 \; \dots \; \mathbf{b}_k], \; X = [\mathbf{x}_1 \; \mathbf{x}_2 \; \dots \; \mathbf{x}_k]$ 이다.

• $\mathbf{b}$ 를 바꿔가면서 여러번 풀면 되는게 아닐까? 라고 생각할 수도 있지만,

x = linalg.solve(A, b, assume_a="gen")

• $\mathbf{b}_1, \dots , \mathbf{b}_k$ 까지 b를 바꿔가며 여러번 반복하면 무의미한 decomposition 을 내부에서 수행하며 work-load 를 낭비하게 된다.
• 특히 $A = LU$ 는 $\sim n^3$ , $LU\mathbf{x} = \mathbf{b}$ 는 $\sim n^2$

• 따라서 $\mathbf{b}$ 벡터들이 주어졌다면 아래를 사용하는게 현명하다.

X = linalg.solve(A, B, assume_a="gen")

• 극단적으로 1000x1000 크기의 행렬을 \(\mathbf{b}_1, \mathbf{b}_2, \dots, \mathbf{b}_{1000}\) 인 1000 개의 행렬 방정식을 푼다고 했을 때
• 각 1000회 반복한 시간과 $B$ 벡터로 묶어서 동시에 푸는 시간을 비교해보면
• 1000 회 반복은 12.54s, 동시에 풀면 0.04s 라는 결과가 나온다.

# 1000회 반복 => 12.54 s
x = linalg.solve(A, b, assume_a="gen")

# 0.04 s
X = linalg.solve(A, B, assume_a="gen")