Hits


Scipy 에서의 Band Matrix 입력

  • 기존 밴드 행렬
  • lower band width = 1, upper band width = 2 인 형태이다.
  • band width 가 행렬 사이즈 n 보다 많이 작다면 (band width « n) 메모리 측면과 계산 효율 측면에서 상당히 유리하게 사용이 가능하다.

Desktop View

  • Scipy 에서의 밴드 포맷

Desktop View

  • column(열) index 를 유지하면서 밴드만 가져와서 가로 형태로 쌓아준다.


  • 일반 행렬을 밴드 행렬로 변환 시키려면 메모리 사용과 함께 귀찮은 작업이 동반되므로 강의에서 사용하는 custom 함수를 사용하도록 하겠다.

  • inp_band.txt 파일 내용

    1
2
3
4
5

    1 2 0 0 0
1 4 1 0 0
5 0 1 2 0
0 1 2 2 1
0 0 2 1 1

1
2
3
4

from custom_band import read_banded

band_a = read_banded("inp_band.txt", (lbw, ubw) , dtype=np.float64, delimiter=",")
print(band_a)

  • 여기서 tuple (lbw,ubw) 는 각 lower band width, upper band width 를 의미한다.

  • band_a 가 출력된 결과물

1
2
3
4

[[0. 2. 1. 2. 1.]
 [1. 4. 1. 2. 1.]
 [1. 0. 2. 1. 0.]
 [5. 1. 2. 0. 0.]]



Band Matrix Solver

  • $A\mathbf{x} = \mathbf{b}$ 방정식을 풀 때 linalg.solve_banded 를 사용하여 풀 수 있다. 여기서 $A$ 행렬이 밴드 행렬일 때 더 유리하다.

  • x = linalg.solve_banded( (lbw, ubw), band_a, b)

  • 기본 알고리즘은
    1. LU decomposition
    1. tridiagonal solver 는 lbw = 1, ubw = 1 일 때 자동으로 판단하여 푼다.


  • 여기서 문제점은.. 행렬의 solution 을 구하기 위해서는 band 행렬을 다시 원래 행렬로 돌려놓는 작업이 필요하다.
  • band_A @ x != b 가 아니라 A @ x = b 로 다시 계산을 해야한다는 것..
  • 이렇게되면 불필요한 계산이 많아지고 메모리적으로 비효율적이다.
  • 따라서 강의에서는 band 행렬과 x 를 계산 가능한 다음과 같은 커스텀 함수를 사용한다.
1
2
3

from custom_band import matmul_banded

bp = matmul_banded( (lbw, ubw), band_a, x )



Positive Definite 행렬의 밴드 행렬 Solver

  • Symmetric/Hermitian 행렬일 경우 다음과 같이 사용한다.
  • 결국 대칭 행렬이기 때문에 한쪽 밴드만 알면되므로 lower = False
  • 기본 알고리즘은 다음과 같다.
    1. Cholesky decomposition
    2. $LDL^T$ decomposition
    3. $U^TDT$ (tridiagonal 일 때)
1

x = linalg.solveh_banded(band_a_h, b, lower = False)


  • Positive Definite 인 경우 절반의 밴드 행렬만 저장하면 되므로 공간복잡도에서도 이점을 가진다.

Desktop View

  • 강의에는 또한 커스텀으로 Positive Definite 밴드 행렬 변환 함수가 존재한다.
1
2
3

from custom_band import read_banded_h

band_a_h = read_banded_h("inp_band.txt", 1, dtype=np.float64, delimiter="," , lower=False)


  • 예시
1
2
3
4
5
6

# band_p07.txt
2 1 0 0 0
1 2 1 0 0
0 1 2 1 0
0 0 1 2 1
0 0 0 1 2

1
2
3
4
5

# band_p07_2.txt
8 2-1j 0 0
2_1j 5 1j 0
0 -1j 9 -2-1j
0 0 -2+1j 6

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

b1 = np.ones((4,), dtype=np.float64)
b2 = np.ones((5,), dtype=np.float64)

band_a1_h = read_banded_h("band_p07.txt", 1, dtype=np.complex128, delimiter=" ", lower=False)

band_a2_h = read_banded_h("band_p07_2.txt", 1, dtype=np.float64, delimiter=" ", lower=False)

print(band_a1_h)

print()

print(band_a2_h)

print()

x1 = linalg.solveh_banded( band_a1_h, b1, lower=False)

x2 = linalg.solveh_banded( band_a2_h, b2, lower=False)

bp1 = matmul_banded_h( 1, band_a1_h, x1, lower=False)
print(np.allclose(bp1, b1))
print(bp1)

print()

bp2 = matmul_banded_h( 1, band_a2_h, x2, lower=False)
print(np.allclose(bp2, b2))
print(bp2)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

# band 행렬로 다음과 같이 나타난다.
[[ 0.+0.j  2.-1.j  0.+1.j -2.-1.j]
 [ 8.+0.j  5.+0.j  9.+0.j  6.+0.j]]

[[0. 1. 1. 1. 1.]
 [2. 2. 2. 2. 2.]]

# 계산 결과값이 근사하다는것을 알 수 있다.

True
[1.+0.00000000e+00j 1.+0.00000000e+00j 1.+0.00000000e+00j
 1.+1.38777878e-17j]

True
[1. 1. 1. 1. 1.]



행렬 계산에서 밴드 행렬과 적합한 Solver 가 필요한가?에 대한 분석

  • 실제 여러 분야에서 행렬 계산을 할 때, row x column 이 수십, 수백 단위가 아니라 수만 단위까지 늘어나는 경우가 많다.
  • 극단적인 예시로, A 행렬이 10000 x 10000 이라고 생각해보면
  • 이 때, A 행렬을 통째로 메모리에 올리면 대략 760MB 정도 된다. 실로 어마어마한 수치이다..
  • 만약 A 행렬을 밴드 행렬로 변환한다면? 156KB 메모리만 필요하다. 대략 5000배 정도 줄어든다.


  • solver 의 경우를 알아보자.

solve(A,b) 일 경우 시간소요
assume_a = “pos” : 3.36 sec
assume_a = “gen” : 3.97 sec

solve_banded 일 경우 시간소요
solveh_banded(band_a_h, b) : 0.00023 sec
solve_banded((1,1), band_a, b) : 0.00029 sec

  • 3초 넘게 차이나는 것을 확인할 수 있다.
  • 따라서 밴드행렬 형태로 사용한다는 것은 시간,공간 복잡도에서 엄청난 이점을 갖는다.



Example 1.

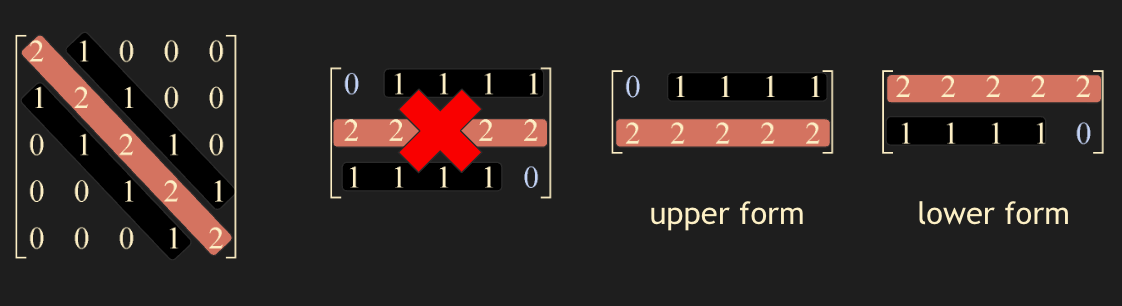
$A = \begin{bmatrix} 2 & 1 & & & \\ 1 & 2 & 1 & & \\ & \ddots & \ddots & \ddots & \\ & & 1 & 2 & 1 \\ & & & 1 & 2 \end{bmatrix}$

$A$ 는 1000x1000 matrix 이다. $A$ 의 밴드 행렬 (upper form) 만들기
밴드 행렬을 사용하여 $A\mathbf{x} = \mathbf{b}$ 해를 구하기
matmul_banded_h 와 np.allclose 를 사용하여 해의 타당성 검증하기


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

import numpy as np
from scipy import linalg
from print_lecture import print_custom as prt
from custom_band import read_banded
from custom_band import matmul_banded
from custom_band import read_banded_h, matmul_banded_h

n = 1000

# 1로 채워진 사이즈 999짜리 밴드

band1 = np.ones((n-1), dtype=np.float64)

# 2로 채워진 사이즈 1000짜리 밴드
band2 = 2*np.ones((n,), dtype=np.float64)

b = np.ones((n,), dtype=np.float64)

# A full 행렬 생성
A_full = np.diag(band2) + np.diag(band1,k=1) + np.diag(band1,k=-1)

# 사이즈 1짜리 zero vector
zr = np.zeros((1,), dtype=np.float64)

# A의 upper band 형태를 만들기 위한 작업
row1 = np.hstack( (zr,band1) ) # 0,1,1,1,......,1
# row2는 band2와 동일하니깐 생략

# upper band 형태
A_band_h = np.vstack( (row1,band2) )

# full matrix로 해를 구하기, 옵션은 일단 생략하였으나, positive definite 성질 사용 가능 (assume_a="pos")
x1 = linalg.solve(A_full,b)

x2 = linalg.solveh_banded(A_band_h,b)

# x1 및 x2 타당성 검증
bp1 = A_full@x1
bp2 = matmul_banded_h(1,A_band_h,x2,lower=False)
print(np.allclose(bp1, b))
print(np.allclose(bp2, b))

1
2

True
True