Numpy & Scipy - 1.6 The Solution of Matrix Equation (General Matrices)

Determinant 구하기

  
from scipy import linalg

scipy 의 linalg 를 import 해주자.

linalg.det(Matrix) 를 사용하면 determinant 를 구해서 반환해준다.
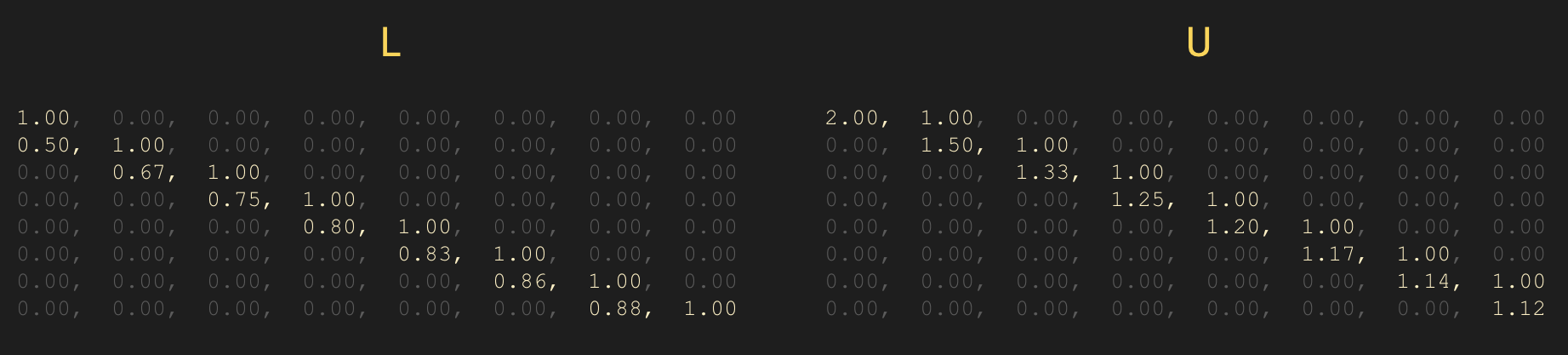
기본적인 알고리즘은 LU Decomposition 을 사용한다. $\quad A = LU$
또한, determinant 계산은 다음과 같이 실행되는데

\[det(A) = det(L*U) = det(L)*det(U) = det(U)\]

사실상 여기서 det(L) 이 diagonal term 들이 전부 1이기 때문에, det(U) 만을 계산하면 된다.
따라서, General Case의 determinant 를 구할 때 선형대수에서 배웠던 Cramer’s Rule 과 같은 방법은 사용하지 않는다.

  
A1 = np.array([[1,5,0],[2,4,-1],[0,-2,0]])
det = linalg.det(A1)

print(det)

A2 = np.array([[1,-4,2],[-2,8,-9],[-1,7,0]])
det = linalg.det(A2)

print(det)

-2.0

15.0

역행렬보다 Ax=b 를 푸는게 더 좋은 이유

$A^{-1}$ 을 구해 해를 찾는 경우
$A^{-1}$ 계산 시간복잡도 : $\sim n^3$
$A^{-1}b$ 계산 시간복잡도 : $\sim n^2$

$A\mathbf{x} = \mathbf{b}$ 방정식을 풀어 해를 찾는 경우
Gauss Elimination : $\sim n^3$
LU decomposition :
$A = LU$ 를 분해하는 시간복잡도 : $\sim n^3$
$LU\mathbf{x} = \mathbf{b}$ 방정식을 푸는 시간복잡도 : $\sim n^2$

둘 다 시간복잡도를 비교하면 엇비슷해보이지만.. 다음과 같은 이유들 때문에 역행렬을 사용하지 않고, $A\mathbf{x} = \mathbf{b}$ 방정식을 푸는 방법을 선호한다.

수치적 정확도
컴퓨터에서는 floating point(부동소수점) 즉 제한된 소수점으로 표현 된다. 역행렬을 통해 계산을 하게 되면 상대적으로 방정식을 풀어 해를 구하는 방법보다는 근사치가 많아지게 되고, 부정확한 결과물이 나오게 된다. 또한 backward error analysis 의 이유 때문에 역행렬을 주로 사용하지 않는다.

Sparse Matrix(희소 행렬) 의 역행렬과 LU Decomposition 의 비교
행렬의 대부분이 0일 경우 그 행렬의 역행렬은 어떻게 될까?
sparse matrix 의 역행렬도 거의 sparse 하지 않을까? 라고 생각했지만.. 현실은 그렇게 녹록치 않았다.
반면, L과 U는 여전히 sparse 한 경우가 많았다.

정리하자면, 특별히 $A^{-1}$ 역행렬이 필요한 경우가 아니라면, $A\mathbf{x} = \mathbf{b}$ 를 풀 때 역행렬을 구하지 말자!

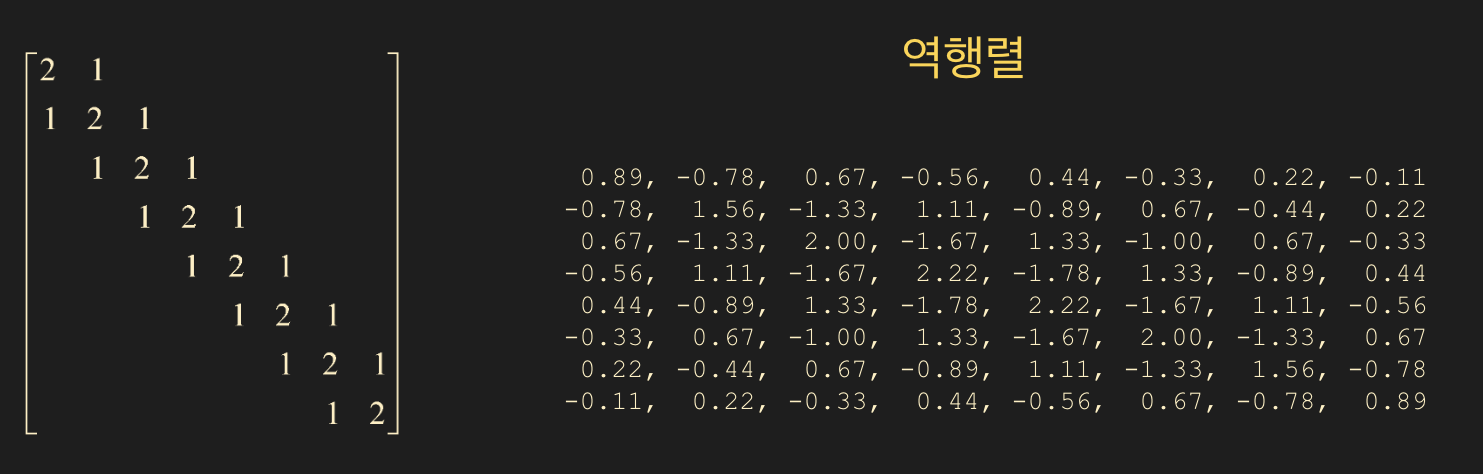
역행렬(Inverse) 구하기

역행렬을 구하는 목적이 $A\mathbf{x} = \mathbf{b}$ 를 푸는거라면 다시 한 번 생각을 해봐야한다.
linalg.inv(matrix) 를 사용하여 역행렬을 구한다.
여기서 파라미터로 입력한 행렬의 역행렬이 없다면? 즉 singular matrix 이면 에러가 발생한다.
기본 알고리즘은 LU decomposition 을 사용하고 $\quad LUA^{-1} = I$ 를 푸는데, backward phase(back substitution) 과정만을 거친다.

  
A1 = np.array([[1,2,1],[2,1,3],[1,3,1]])
inv_a1 = linalg.inv(A1)

prt(inv_a1, fmt="%0.2f")

 8.00, -1.00, -5.00
-1.00,  0.00,  1.00
-5.00,  1.00,  3.00

Ax = b 행렬 방정식 풀기

$A\mathbf{x} = \mathbf{b}$ 를 푼다는 것, 즉 해를 구한다는 것은 $\mathbf{x}$ 를 구하는것과 동일하므로
x = linalg.solve(A, b, assume_a=”gen”) 함수를 사용하면 된다.
여기서 assume_a 에 입력하는 파라미터로는 4가지 타입이 입력이 가능하다.

gen
일반적인 solver 이다. 어떤 행렬 타입(symmetric, hermitian..) 인지 모를 경우 주로 사용한다.
LU decomposition 으로 푼다. $\quad A = LU$

sym
symmetric, complex symmetric matrix 일 때 사용이 가능하다. 여기서 complex symmetric 은 hermitian 이 아님에 주의하자.
symmetric matrix 의 성질은 $\; A = A^T \;$ 이다.
diagonal pivoting $\quad A = LDL^T \mbox{(block diagonal)}$ 를 사용한다.

her
hermitian matrix 일 때 사용한다. $\quad A = A^$ (conjugate)
diagonal pivoting $\quad A = LDL^$ 으로 푼다.

pos
positive definite 일 때 사용한다. quadratic form $\mathbf{x}^TA\mathbf{x} > 0$ 을 의미. 알고리즘은 Cholesky Decomposition $\quad A = R^TR = LL^T$

여기서 주의할 점은 assume_a 를 잘못 설정하여도 에러 표시를 하지 않고 잘못된 결과를 반환해주니 주의 할 것.. 따라서 보통 gen 을 주로 사용한다.
matrix 성질을 잘 이해하면 assume_a 옵션을 사용하는게 좋다. (연산 속도에 이점)

  
b = np.ones((3,), dtype=np.float64)

# singular (not invertible)
A_sing = np.array([[1,3,4],[-4,2,-6],[-3,-2,-7]])

# gen (general)
A_gen = np.array([[0,1,2],[1,0,3],[4,-3,8]])

# sym (symmetric)
A_sym = np.array([[1,2,1],[2,1,3],[1,3,1]])

# sym complex (symmetric complex)
A_sym_c = np.array([[1, 2-1j, 1+2j],[2-1j, 1, 3],[1+2j, 3,1]])

# her (hermitian)
A_her = np.array([[1, 2+1j, 1-2j],[2-1j, 1, 3],[1+2j, 3,1]])

# pos (positive definite)
A_pos = np.array([[2, -1, 0],[-1,2,-1],[0,-1,2]])

singular
singular matrix 이기 때문에 에러 발생

  
x = linalg.solve(A_sing, b) 

numpy.linalg.LinAlgError: Matrix is singular.

gen
Ax = b -> Ax - b = 0 임을 판별하기 위해 마지막 줄에 추가.

  
x = linalg.solve(A_gen, b)

prt(x, fmt="%0.5e")
print()
prt(A_gen @ x - b , fmt="%0.5e")

00000e+00,  1.00000e+00,  0.00000e+00

00000e+00,  0.00000e+00,  0.00000e+00

sym
sym 과 gen 의 차이점은 푸는 알고리즘에 차이가 존재하는데.
우리가 구하는 x 는 근사값이라는 것을 인지해두자. gen 으로 LU decomposition, sym 으로 diagonal pivoting 을 사용하여 계사한 결과값에 오차가 발생한다.

  
x1 = linalg.solve(A_sym, b) # default 로는 gen
x2 = linalg.solve(A_sym, b, assume_a="sym")

prt(x1, fmt="%0.5e")
print()
prt(A_sym @ x1 - b , fmt="%0.5e")

prt(x2, fmt="%0.5e")
print()
prt(A_sym @ x2 - b , fmt="%0.5e")

  
 # gen
 2.00000e+00,  0.00000e+00, -1.00000e+00

 0.00000e+00,  0.00000e+00,  0.00000e+00

# sym
 2.00000e+00, -2.77556e-17, -1.00000e+00

 0.00000e+00,  0.00000e+00,  0.00000e+00

her

  
x = linalg.solve(A_her, b, assume_a="her")

prt(x, fmt="%0.5e")
print()
prt(A_her @ x - b , fmt="%0.5e")

( 1.11111e-01+1.11111e-01j), ( 3.33333e-01-1.11111e-01j), ( 1.11111e-01+1.11022e-16j)

( 0.00000e+00+2.77556e-17j), (-4.44089e-16+1.94289e-16j), ( 2.22045e-16-1.66533e-16j)

여기서 e-16 은 10의 -16승이기 때문에 0에 가깝다.

pos

  
x1 = linalg.solve(A_pos, b, assume_a="gen")
x2 = linalg.solve(A_pos, b, assume_a="pos")

prt(x1, fmt="%0.5e")
print()
prt(A_pos @ x1 - b , fmt="%0.5e")

prt(x2, fmt="%0.5e")
print()
prt(A_pos @ x2 - b , fmt="%0.5e")

  
# gen
 1.50000e+00,  2.00000e+00,  1.50000e+00

 0.00000e+00,  2.22045e-16, -4.44089e-16

# pos
 1.50000e+00,  2.00000e+00,  1.50000e+00

-8.88178e-16,  1.55431e-15, -4.44089e-16

Triangular Matrix Solver

마찬가지로 $A\mathbf{x} = \mathbf{b}$ 를 풀지만 행렬 $A$ 가 lower triangular matrix, upper triangular matrix 일 경우만 가능하다.
backward phase (backsubstitution) 의 연산만 필요하다.
x = linalg.solve_triangular(A, b, lower=False)
여기서 lower 파라미터는 lower 이면 True, upper 이면 False

  
A = np.array([[1,0,0,0],[1,4,0,0],[5,0,1,0],[8,1,-2,2]], dtype=np.float64)
b = np.array([1,2,3,4],dtype=np.float64)

x = linalg.solve_triangular(A, b, lower=True)

prt(x, fmt="%0.5e")

 1.00000e+00,  2.50000e-01, -2.00000e+00, -4.12500e+00

구한 해가 정확한가?

우리가 $A\mathbf{x} = \mathbf{b}$ 를 풀면서 $\mathbf{x}$ 의 해를 구한 결과는 수치적 계산으로 근사된 값이다.
Ax 와 b 가 충분히 비슷한가? == Ax-b 가 충분히 0에 가까운지? 와 같다.
따라서 np.allclose 함수를 사용하여 $A\mathbf{x} - \mathbf{b}$ 와 np.zeros 를 통해 만든 0 행렬을 비교하면 된다.

  
A = np.array([[2,-1,0],[-1,2,-1],[0,-1,2]], dtype=np.float64)
b = np.ones((3,), dtype=np.float64)

x = linalg.solve(A, b, assume_a="pos")

prt(x, fmt="%0.5e")
print()
prt(A@x-b, fmt="%0.5e")

zr = np.zeros((3,), dtype=np.float64)

bool_close = np.allclose(A@x-b, zr)
print(bool_close)

 1.50000e+00,  2.00000e+00,  1.50000e+00

-8.88178e-16,  1.55431e-15, -4.44089e-16
True

Example 1.
$A = \begin{bmatrix} 1 & 1/2 & 1/3 & \dots & 1/9 & 1/10 \\ 1/2 & 1/3 & 1/4 & \dots & 1/10 & 1/11 \\ 1/3 & 1/4 & 1/5 & \dots & 1/11 & 1/12 \\ \vdots & \ddots & \ddots & & & \\ 1/9 & 1/10 & & & 1/17 & 1/18 \\ 1/10 & 1/11 & \dots & \dots & 1/18 & 1/19 \end{bmatrix} $
10x10 Hilbert 행렬을 linalg.hilbert(10)로 만들수 있다. A에 해당 행렬을 저장하기.
A의 역행렬을 inv_A에 저장하기
x1 = inv_A @ b 로 구하기
x2를 linalg.solve를 사용하여 구하기 (gen)
A@x1 - b 를 커스텀 출력으로 소수점 15자리까지 출력해보기 (floating)
A@x2 - b 를 커스텀 출력으로 소수점 15자리까지 출력해보기 (floating)
A@x1 - b 과 A@x2 - b를 allclose를 활용하여 zero vector와 비교해보기

풀이
hilbert matrix 는 수치해석 방법론적으로 다루기 매우 까다로운 행렬이다. 사이즈가 커지면 커질 수록 풀기 어렵다.
우리가 이론수업으로 배웠지만 inverse 형태로 푸는게 정확도 측면에서 안좋다고 배웠었다.

  
A = linalg.hilbert(10)
b = np.ones((10,), dtype=np.float64)

# Hilbert 행렬
prt(A, fmt="%0.5f")

A_inv = linalg.inv(A)

x1 = A_inv @ b

print()

x2 = linalg.solve(A, b, assume_a="gen")

prt(A @ x1 - b, fmt="%0.15e")
print()
prt(A @ x2 - b, fmt="%0.15e")
print()

zr = np.zeros((10,), dtype=np.float64)

bool_close1 = np.allclose(A @ x1 - b, zr)
print(bool_close1)

bool_close2 = np.allclose(A @ x2 - b, zr)
print(bool_close2)

Hilbert Matrix 를 출력한 모습

00000,  0.50000,  0.33333,  0.25000,  0.20000,  0.16667,  0.14286,  0.12500,  0.11111,  0.10000
50000,  0.33333,  0.25000,  0.20000,  0.16667,  0.14286,  0.12500,  0.11111,  0.10000,  0.09091
33333,  0.25000,  0.20000,  0.16667,  0.14286,  0.12500,  0.11111,  0.10000,  0.09091,  0.08333
25000,  0.20000,  0.16667,  0.14286,  0.12500,  0.11111,  0.10000,  0.09091,  0.08333,  0.07692
20000,  0.16667,  0.14286,  0.12500,  0.11111,  0.10000,  0.09091,  0.08333,  0.07692,  0.07143
16667,  0.14286,  0.12500,  0.11111,  0.10000,  0.09091,  0.08333,  0.07692,  0.07143,  0.06667
14286,  0.12500,  0.11111,  0.10000,  0.09091,  0.08333,  0.07692,  0.07143,  0.06667,  0.06250
12500,  0.11111,  0.10000,  0.09091,  0.08333,  0.07692,  0.07143,  0.06667,  0.06250,  0.05882
11111,  0.10000,  0.09091,  0.08333,  0.07692,  0.07143,  0.06667,  0.06250,  0.05882,  0.05556
10000,  0.09091,  0.08333,  0.07692,  0.07143,  0.06667,  0.06250,  0.05882,  0.05556,  0.05263

역행렬을 통해 해를 구한 결과값과 np.solve (gen) 을 통해 구한 결과값의 비교

-5.384686879750245e-05, -4.824035864248177e-05, -4.365437722742005e-05, -3.984553430069759e-05, -3.663714443313815e-05, -3.390060580654719e-05, -3.154054138576612e-05, -2.948524204493541e-05, -2.767985240692550e-05, -2.608172012175114e-05

 1.768403201651836e-10,  2.589735093039280e-10,  1.027888885118955e-11, -5.332401187274627e-13, -2.094682205466825e-10, -1.216354794664198e-10,  8.731149137020111e-11,  4.546962806273314e-11,  5.050826423769195e-11, -6.052347512053302e-11

False
True

Numpy & Scipy - 1.6 The Solution of Matrix Equation (General Matrices)

Determinant 구하기

역행렬보다 Ax=b 를 푸는게 더 좋은 이유

역행렬(Inverse) 구하기

Ax = b 행렬 방정식 풀기

Triangular Matrix Solver

구한 해가 정확한가?

Trending Tags