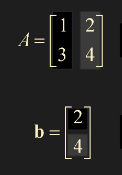같은 사이즈의 행렬,벡터의 덧셈 뺄셈
$A = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}$ $B = \begin{bmatrix} 5 & 6 \\ 7 & 8 \end{bmatrix}$
1
2
3
4
5
6
7
| A = np.array([[1,2], [3,4]])
B = np.array([[5,6],[7,8]])
C = A + B
C = A - B
|
- 벡터(1D array)도 마찬가지 덧셈,뺄셈이 가능하다.
- shape 만 똑같으면 문제가 없다.
사이즈가 큰 행렬 쉽게 만들기
$ A = \begin{bmatrix} 2 & 1 & 0 & 0 & 0 \\ -1 & 2 & 1 & 0 & 0 \\ 0 & -1 & 2 & 1 & 0 \\ 0 & 0 & -1 & 2 & 1 \\ 0 & 0 & 0 & -1 & 2 \end{bmatrix} = \begin{bmatrix} 0 & 0 & 0 & 0 & 0 \\ -1 & 0 & 0 & 0 & 0 \\ 0 & -1 & 0 & 0 & 0 \\ 0 & 0 & -1 & 0 & 0 \\ 0 & 0 & 0 & -1 & 0 \end{bmatrix} + \begin{bmatrix} 2 & 0 & 0 & 0 & 0 \\ 0 & 2 & 0 & 0 & 0 \\ 0 & 0 & 2 & 0 & 0 \\ 0 & 0 & 0 & 2 & 0 \\ 0 & 0 & 0 & 0 & 2 \end{bmatrix} + \begin{bmatrix} 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 \end{bmatrix} $
- 여기서 band 별로 np.ones 를 활용해서 1D array 로 뽑아낸 뒤 스칼라값을 곱해주자.
$k = -1$ 인 경우
$ b_1 = \begin{bmatrix} -1 & -1 & -1 & -1 \end{bmatrix} $
1
| b1 = (-1)*np.ones((4,))
|
$k = 0$ 인 경우
$ b_2 = \begin{bmatrix} 2 & 2 & 2 & 2 & 2 \end{bmatrix} $
$k = 1$ 인 경우
$ b_3 = \begin{bmatrix} 1 & 1 & 1 & 1 \end{bmatrix} $
- 이후 np.diag 기능을 활용하여 1D array 들을 각각 최대 사이즈(k=0)를 기준으로 한 행렬로 만들어준 뒤 더해주면 된다.
1
2
3
| A = np.diag(b1, k=-1) + np.diag(b2, k=0) + np.diag(b3, k=1)
print(A)
|
1
2
3
4
5
| [[ 2. 1. 0. 0. 0.]
[-1. 2. 1. 0. 0.]
[ 0. -1. 2. 1. 0.]
[ 0. 0. -1. 2. 1.]
[ 0. 0. 0. -1. 2.]]
|
스칼라와 행렬의 덧셈(r + A)
- 수학적으로는 말이 안되지만, 파이썬에서는 가능하다..
- 모든 entry 에 scalar 를 더해준다. 벡터도 마찬가지.
1
2
3
4
5
6
7
| A = np.array([[1,2],[3,4]])
r = 5
result = r + A # = A + r
print(result)
|
행렬과 행렬의 곱셈과 나눗셈 (A * B) (A / B)
- matrix multiplication 이 아님에 주의하자. A @ B, np.matmul 과 전혀 다르다!!
- shape 이 같은 행렬끼리 곱셈을 할 수 있다.
- 같은 index 의 entry 들을 곱해서 결과로 반환한다. 벡터도 마찬가지
1
2
3
4
5
6
| A = np.array([[1,2],[3,4]])
B = np.array([[5,6],[7,8]])
result = A * B # = B * A
print(result)
|
- 나눗셈도 마찬가지이다.
- 역행렬을 의미하는게 아니라 단순히 나눗셈이다.
1
2
3
4
5
6
| A = np.array([[1,2],[3,4]])
B = np.array([[5,6],[7,8]])
result = A / B # = B / A
print(result)
|
1
2
| [[0.2 0.33333333]
[0.42857143 0.5 ]]
|
행렬과 벡터의 곱셈과 나눗셈 (A * b) (A / b)
- matrix-vector product 가 아님에 주의하자.
- shape 이 다른 상황인데 가능하다..
- 행렬의 열개수와 벡터의 사이즈가 동일해야한다. (A.shape[1] == b.shape[0])
- 나눗셈의 경우 A/b 와 b/A 는 결과값이 다르다. 연산 방법 자체가 다르기 때문
- 위 사진의 같은 색상 영역끼리 곱셈,나눗셈이 이루어짐
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| A = np.array([[1,2],[3,4]])
b = np.array([2,4])
result = A * b
print(result)
result = A / b
print(result)
result = b / A # = b * (1 / A) 라고 생각하면된다.
print(result)
|
1
2
3
4
5
6
7
8
| [[ 2 8]
[ 6 16]]
[[0.5 0.5]
[1.5 1. ]]
[[2. 2. ]
[0.66666667 1. ]]
|
index array 를 사용하여 행렬 일부 재구축하기
1
2
3
| A = np.array([[1,2,3,4,5],[6,7,8,9,10],[11,12,13,14,15],[-1,-2,-3,-4,-5]])
print(A)
|
1
2
3
4
5
6
7
8
| what_i_want = A[[1,2,0,3], : ]
# or
idx = [1,2,0,3]
what_i_want = A[idx, :]
print(what_i_want)
|
1
2
3
4
5
6
7
8
9
10
11
| # matrix A
[[ 1 2 3 4 5]
[ 6 7 8 9 10]
[11 12 13 14 15]
[-1 -2 -3 -4 -5]]
# index array
[[ 6 7 8 9 10]
[11 12 13 14 15]
[ 1 2 3 4 5]
[-1 -2 -3 -4 -5]]
|
1
2
3
4
5
| idx = [2,1]
what_i_want = A[idx, :]
print(what_i_want)
|
1
2
| [[11 12 13 14 15]
[ 6 7 8 9 10]]
|
1
2
3
4
5
| idx = [4,1,2]
what_i_want = A[:, idx]
print(what_i_want)
|
1
2
3
4
| [[ 5 2 3]
[10 7 8]
[15 12 13]
[-5 -2 -3]]
|
1
2
3
4
5
6
| idx_r = [2,3,0] # row
idx_c = [2,1,3] # column
what_i_want = A[idx_r, :][:, idx_c] # = A[:, idx_c][idx_r, :]
print(what_i_want)
|
1
2
3
| [[13 12 14]
[-3 -2 -4]
[ 3 2 4]]
|