Machine Learning - Gradient Descent

해당 포스트는 Andrew Ng 교수님의 Machine Learning Specialization 특화 과정에 대한 정리 내용을 참고하였습니다.

Gradient Descent - 경사하강법

$\underset{w,b}{\mbox{min}} \; J(w,b)$ 를 위해 gradient descent (경사하강법)이라는 알고리즘을 사용한다.
경사하강법은 머신러닝의 모든 곳에서 사용된다. 선형 회귀 뿐만 아니라 딥러닝 모델같은 최첨단 신경망 모델을 훈련시킬때도 사용된다.
$J(w,b)$ 는 선형 회귀를 위한 비용함수이지만, 경사하강법은 선형회귀 뿐만 아니라 모든 함수를 최소화하는데 사용할 수 있는 알고리즘이다.

\[\large{\underset{w_1, \dots, w_n, b} {\mbox{min}} \; J(w_1, w_2, \dots, w_n, b)}\]

경사하강법은 매개변수가 두 개 이상인 모델에서 적용이 가능하며, $w_1, \dots, b$ 까지의 값을 선택하여 $J$ 의 가능한 가장 작은 값을 얻으려는 알고리즘이다.

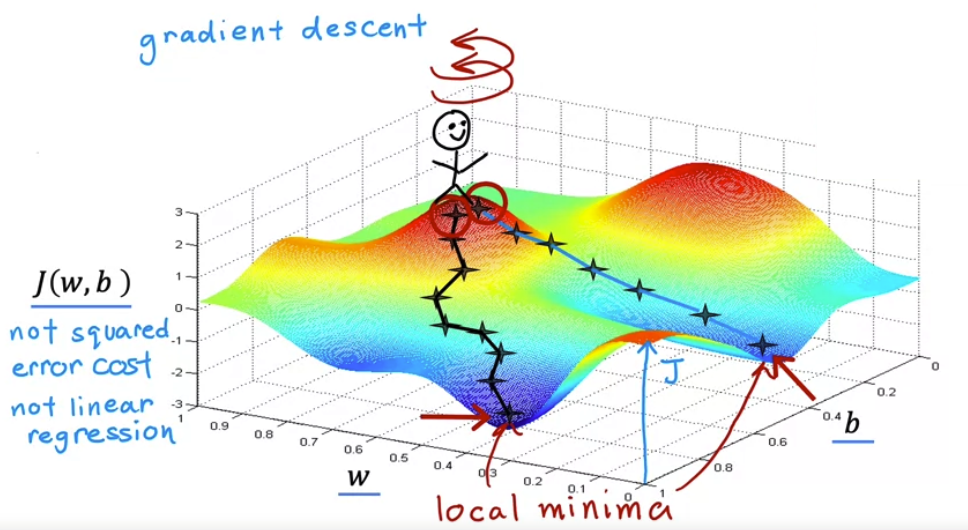
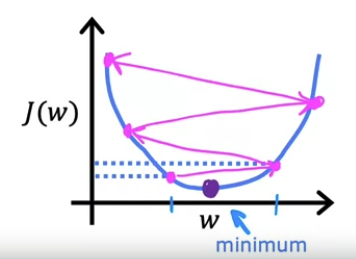
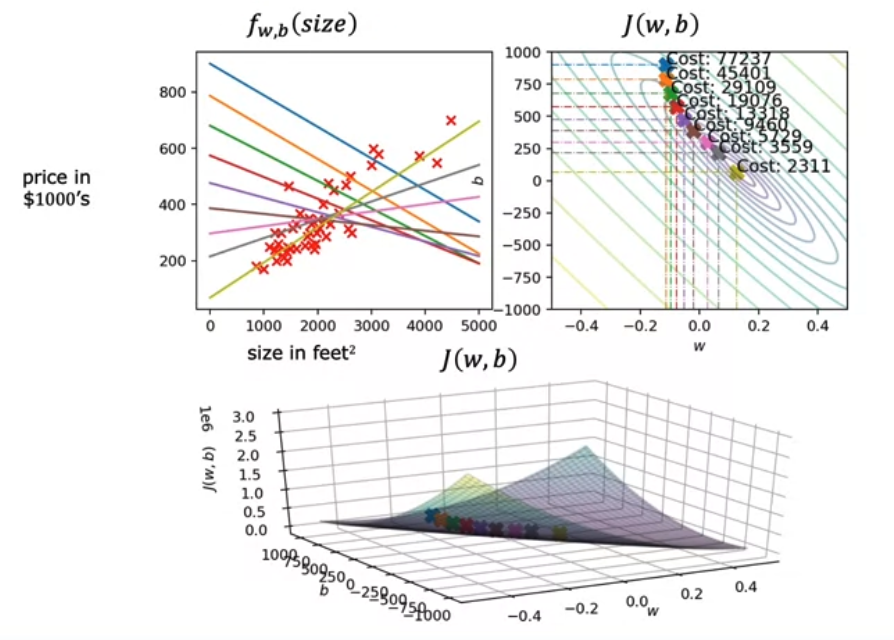
다음은 $J(w,b)$ 의 복잡한 표면도를 나타낸 그림이다. 경사하강법이 어떻게 작동하는지 시각화하여 살펴보자.

위 함수는 Squared Error Cost Function (제곱 오차 비용 함수)가 아니다. 제곱 오차 비용 함수를 사용한 선형 회귀 분석의 경우 항상 이차함수(2D) 모양이나 positive definite 모양(3D)이 된다.
하지만 경사하강법은 신경망 모델을 훈련시킬 때 얻을 수 있는 일종의 비용함수 이므로 모양이 다르다.

매개변수 $w, b$ 의 시작값을 선택하면 표면에서 시작점을 선택할 수 있다.
파란 음영들이 보이는데 이들을 local minima (지역 최솟값 or 국소 최솟값)이라고 한다.
첫 번째 local minima 에 도달하면 경사하강법을 통해 다른 local minima 에 도달할 수 없다.
작은 스텝을 밟을지, 큰 스텝을 밟을지를 learning rate 가 결정한다.
즉, 경사하강법은 local minina (지역 최솟값)을 향해 얼마만큼의 leraning rate 와 direction 을 찾아서 나아가는 것이다.

Gradient Descent Algorithm - 경사하강법 알고리즘

Repeat Until Convergence! (다음 알고리즘을 수렴할 때 까지 반복해야한다.)

\[\large{w = w - \alpha {\partial \over \partial w} J(w,b)}\] \[\large{b = b - \alpha {\partial \over \partial b} J(w,b)}\]

\[\mbox{Simultaneously update w and b}\]

여기서 $\alpha$ 를 learning rate (학습률)이라고 한다.
비용함수 $J(w,b)$ 에 대해 $w$ 만 미분을 취하는 편도함수이다.
$w, b$ 는 항상 동시에 업데이트 해야한다.

Correct : Simultaenous update
$\large{\mbox{tmp_w} = w - \alpha {\partial \over \partial w} J(w,b)}$
$\large{\mbox{tmp_b} = b - \alpha {\partial \over \partial b} J(w,b)}$
$\large{w = \mbox{tmp_w}}$
$\large{b = \mbox{tmp_b}}$

Incorrect
$\large{\mbox{tmp_w} = w - \alpha {\partial \over \partial w} J(w,b)}$
$\large{w = \mbox{tmp_w}}$
$\large{\mbox{tmp_b} = b - \alpha {\partial \over \partial b} J(w,b)}$
$\large{b = \mbox{tmp_b}}$

Gradient Descent Intuition - 경사하강법 직관

learning rate 와 편도함수의 작동원리, 그리고 두 개를 곱하면 매개변수 $w$ 와 $b$ 가 업데이트 되는 이유를 좀 더 직관적으로 살펴보자.
이를 위해 cost function 에서의 예시 처럼 매개변수 $b = 0$ 으로 두고, $w$ 에 대해서만 살펴보면

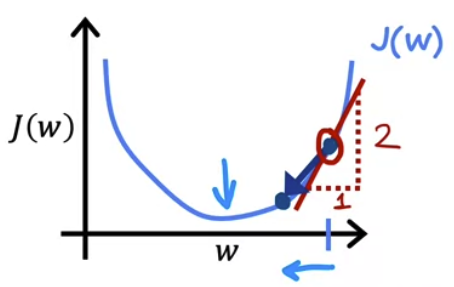
$J(w)$ 를 미분한것은 접선의 기울기를 뜻하며 직선의 특성만 봐도 오른쪽으로 기울었기 때문에 양수임을 의미한다.
따라서 $\large{w = w - \alpha {\partial \over \partial w} J(w,b)}$ 에서 도함수 부분인 $\large{ {\partial \over \partial w} J(w,b)}$ 는 양수이다.

\[\large{ {\partial \over \partial w} J(w,b)} > 0\] \[\large{w = w - \alpha \dot (\mbox{positive number})}\]

learning rate $\alpha$ 는 항상 양수이고 0보다 크다. 그리고 여기서 도함수 역시 양수이므로 $w$ 에서 learning rate 와 접선의 기울기 값을 곱한 것을 빼면 $w$ 는 더 작은 값을 얻게된다.
즉, 그래프에서 왼쪽으로 계속 이동하게 된다. 따라서 비용 $J$ 가 감소하고 $J$ 의 최소값에 가까워지므로 경사하강법이 올바르게 작동한다고 볼 수 있다.

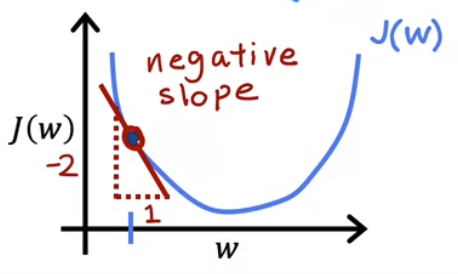
마찬가지로, 반대의 경우 즉 접선의 기울기가 음수인 경우도 존재한다.

\[\large{ {\partial \over \partial w} J(w,b)} < 0\] \[\large{w = w - \alpha \dot (\mbox{negative number})}\]

도함수 부분이 음수이고 $w$ 값은 점점 증가하게 되고 그래프에서 오른쪽으로 이동하게 되며 $J$ 의 최소값에 가까워진다.

Learning Rate - 학습률

이동하는 방향을 알게 되었으니 이젠 얼마만큼 이동을 시키는지 결정하는 learning rate $\alpha$ 에 대해 살펴보자.
learning rate $\alpha$ 값의 선택은 경사하강법 구현의 효율성에 큰 영향을 미친다.
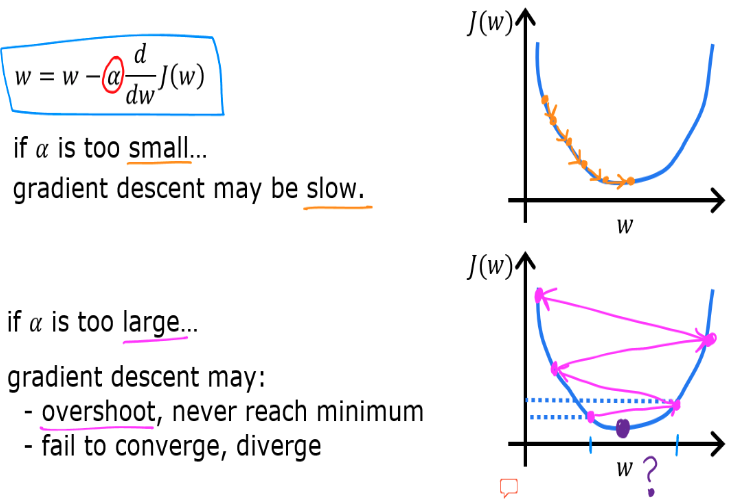
특히 $\alpha$ 가 너무 작거나 혹은 너무 클 경우 어떻게 될까? 위에서 살펴봤던 $J(w)$ 그래프를 예시로 들어보자.

learning rate 가 너무 작은 수치이면 미분항에 아주 작은 수가 곱해지게 된다. (0.000000001 처럼 작은 수)
아주 작은 스텝들을 무수히 많이 실행하면 결과적으로 이 프로세스는 비용 $J$ 는 줄어들게 되지만 엄청나게 느려진다.
minimum 에 도달하기 위해 많은 단계가 필요하다는 것이며, learning rate 가 낮으면 Gradient Descent 는 매우 느려진다.

반대로 learning rate 가 너무 큰 수치이면 어떻게 될까?
아주 큰 단계를 업데이트하여 minimum 을 넘어서버릴 수도 있다. 이는 결과적으로 비용 $J$ 가 더 증가 해버리게 된다.
learning rate 가 너무 크면 minimum 에 converge(수렴)하지 못하고 diverge(발산)해버린다.

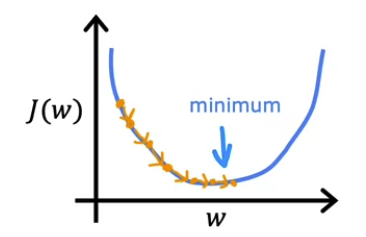
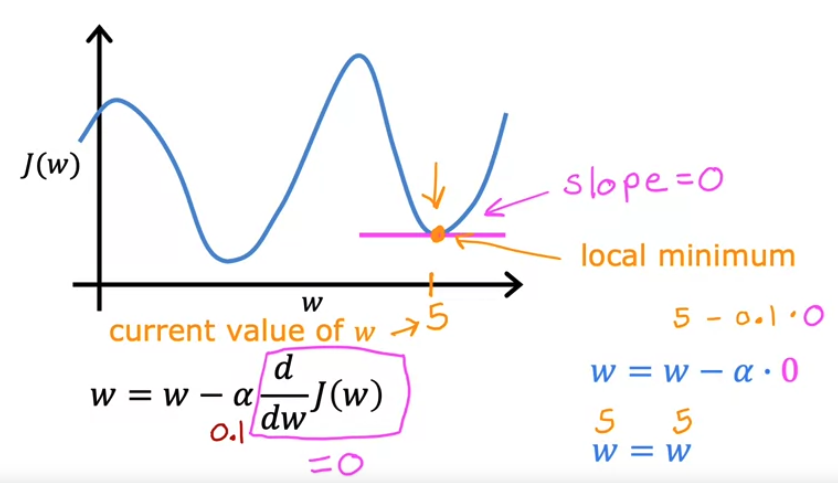
만약, 경사하강법을 통해 local minima (국소 최솟값)에 도달했을 때 다시 경사하강법을 한단계 더 진행해도 괜찮을까?

주황색 점 부분이 현재 $w$ 의 값이고, local minimum 이라고 했을 때
이 지점에서 미분을 진행하면 $w = w - \alpha {d \over dw} J(w)$ 에서 ${d \over dw} J(w) = 0$
즉 접선의 기울기는 0이다. 따라서, 더 이상 경사하강법을 진행할 수가 없다.
여기서 우리는 learning rate $\alpha$ 보다 접선의 기울기를 구하는 미분값이 전체적인 경사하강법에 더 큰 영향을 끼친다는것을 확인 할 수있다.

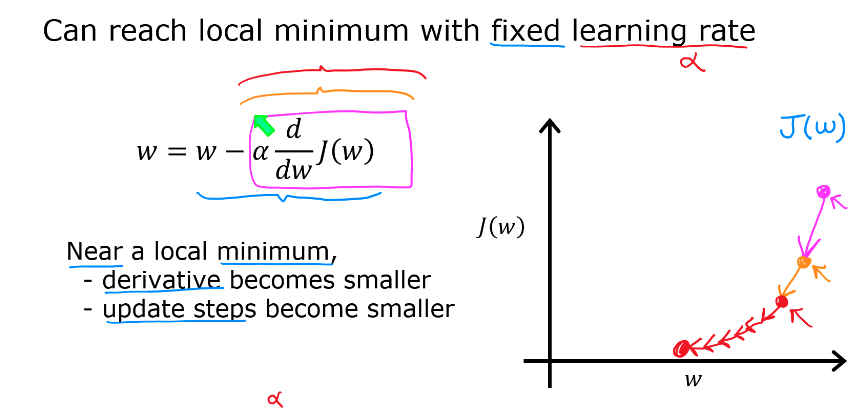
그렇다면 learning rate 값을 고정하고 접선의 기울기가 그래프를 따라 자동으로 감소하거나 증가한다는 것을 발견할 수 있다.

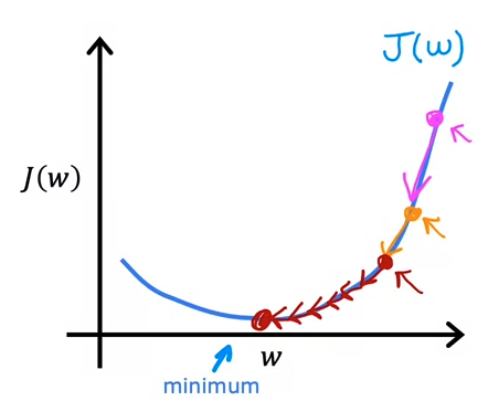
위 그래프를 보면

\[w = w - \alpha {d \over dw} J(w)\]

해당 식에서 연속적으로 미분을 진행하면 경사하강법이 진행될 수록 더 작은 단계가 자동적으로 수행된다는것을 확인할 수 있다.
즉, learning rate $\alpha$ 가 고정된 값으로 유지되더라도 매 업데이트 단계마다 local minima 에 접근하면 도함수가 자동으로 작아진다는 성질을 발견할 수 있다.

Gradient Descent for Linear Regression - 선형회귀를 위한 경사하강법

Linear regression model

\[\large{f_{w,b} (x) = wx + b}\]

Cost function

\[\large{J(w,b) = \frac{1}{2m} \sum\limits_{i = 1}^{m} (f_{w,b}(x^{(i)}) - y^{(i)})^2}\]

Gradient descent algorithm

\[\mbox{repeat until convergence : }\] \[\large{ w = w - \alpha {\partial \over \partial w} J(w,b)}\] \[\large{ b = b - \alpha {\partial \over \partial b} J(w,b)}\]

위 도함수들을 계산해보면 다음과 같이 나온다.

$w = w - \alpha {\partial \over \partial w} J(w,b)$ 풀이

\[{\partial \over \partial w} J(w,b) = \frac{\partial}{\partial w} \frac{1}{2m} \sum\limits_{i = 1}^{m} (f_{w,b} (x^{(i)}) - y^{(i)})^2\] \[= \frac{\partial}{\partial w} \frac{1}{2m} \sum\limits_{i = 1}^{m} (wx^{(i)} + b - y^{(i)})^2\] \[= \frac{1}{2m} \sum\limits_{i = 1}^{m} (wx^{(i)} + b - y^{(i)})2x^{(i)} = \frac{1}{m} \sum\limits_{i = 1}^{m} (wx^{(i)} + b - y^{(i)})x^{(i)}\] \[= \frac{1}{m} \sum\limits_{i = 1}^{m} (f_{w,b}(x^{(i)}) - y^{(i)})x^{(i)}\]

$b = b - \alpha {\partial \over \partial b} J(w,b)$ 풀이

\[{\partial \over \partial b} J(w,b) = \frac{\partial}{\partial b} \frac{1}{2m} \sum\limits_{i = 1}^{m} (f_{w,b} (x^{(i)}) - y^{(i)})^2\] \[= \frac{\partial}{\partial b} \frac{1}{2m} \sum\limits_{i = 1}^{m} (wx^{(i)} + b - y^{(i)})^2\] \[= \frac{1}{2m} \sum\limits_{i = 1}^{m} (wx^{(i)} + b - y^{(i)})2 = \frac{1}{m} \sum\limits_{i = 1}^{m} (wx^{(i)} + b - y^{(i)})\] \[= \frac{1}{m} \sum\limits_{i = 1}^{m} (f_{w,b}(x^{(i)}) - y^{(i)})\]

따라서 선형회귀에서의 경사하강법 알고리즘은 다음과 같이 표현할 수 있다.

\[\large{\mbox{repeat until convergence : }}\] \[\large{w = w - \alpha \frac{\partial}{\partial w} J(w,b) = w - \alpha \frac{1}{m} \sum\limits_{i = 1}^{m} (f_{w,b} (x^{(i)}) - y^{(i)})x^{(i)}}\] \[\large{b = b - \alpha \frac{\partial}{\partial b} J(w,b) = b - \alpha \frac{1}{m} \sum\limits_{i = 1}^{m} (f_{w,b} (x^{(i)}) - y^{(i)})}\] \[\large{\mbox{Update} \; w \; \mbox{and} \; b \; \mbox{simultaneously}}\]

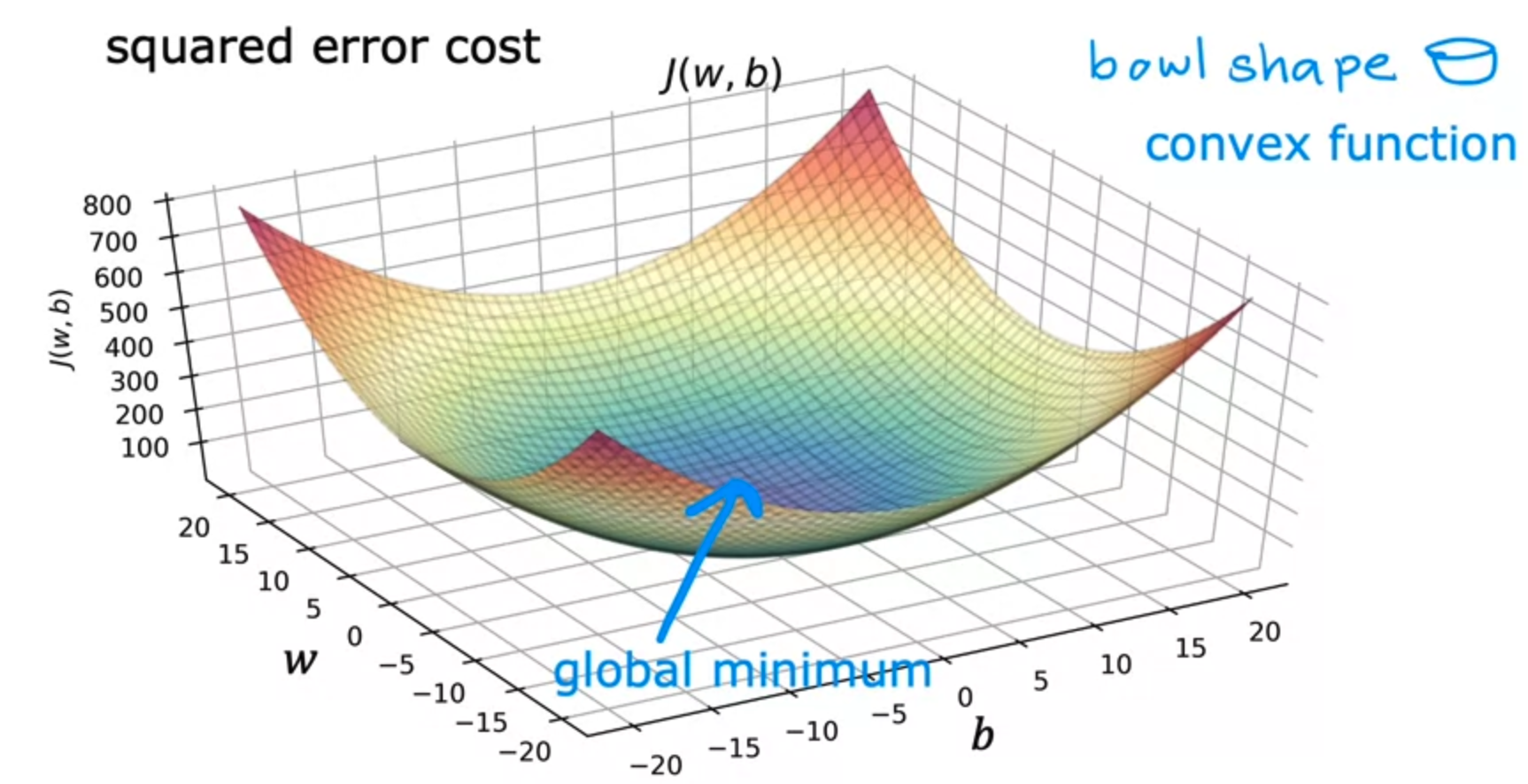
또한 linear regression 과 함께 squared error cost function 을 사용할 경우 cost function 은 local minima 를 여러개 갖지 않으며
단 하나만을 갖는데 이를 global minimum 이라고 부른다.
그리고, 이런 함수를 볼록함수 또는 convex function 이라고 부르며 그래프는 다음과 같다.

convex function 에서 gradient descent 를 구현할 때 가장 유용한 특성중 하나는 learning rate $\alpha$ 를 적절하게 선택하면 항상 global minimum 으로 converge(수렴)한다는 것이다.

앞서 등고선도를 표현한 실습을 통해 실제로 경사하강법을 실행하면 어떻게 되는지 알아보자.
여기서는 $w = -0.1$ , $b = 900$ 으로 초기화하여 경사하강법을 실행했다.
따라서 $f(x) = -0.1x + 900$ 에 해당한다.

경사하강법 업데이트에 따른 직선의 변화를 살펴보면 결국 데이터 집합들에 딱 맞는 직선으로 피팅이 된다.

위와 같이 일괄 경사하강법, 즉 training set 의 모든 예제에 대해 경사하강법을 실행하는 경우를
“Batch” Gradient Descent 라고 한다.
“Batch” : Each step of gradient descent uses all the training examples.
즉, 선형회귀에서는 일괄 경사하강법을 사용한다.

실습

  
import math, copy
import numpy as np
import matplotlib.pyplot as plt
plt.style.use('./deeplearning.mplstyle')
from lab_utils_uni import plt_house_x, plt_contour_wgrad, plt_divergence, plt_gradients

# Load our data set
x_train = np.array([1.0, 2.0])   #features
y_train = np.array([300.0, 500.0])   #target value

#Function to calculate the cost
def compute_cost(x, y, w, b):
   
    m = x.shape[0] 
    cost = 0
    
    for i in range(m):
        f_wb = w * x[i] + b
        cost = cost + (f_wb - y[i])**2
    total_cost = 1 / (2 * m) * cost

    return total_cost

위 내용까지는 cost function 내용과 똑같음

Gradient descent summary
우리는 경사 하강법 강의를 통해 입력 $x^{(i)}$ 를 예측하는 선형 모델 $f_{w,b} (x^{(i)})$ 를 개발했다.

\[f_{w,b} (x^{(i)}) = wx^{(i)} + b \tag{1}\]

선형 회귀에서는 입력 훈련 데이터를 사용하여 매개변수 $w,b$ 를 맞추기 위한 예측값 $f_{w,b} (x^{(i)})$ 와 실제 데이터 $y^{(i)}$ 간의 오차를 최소화하는 측정값을 사용한다.
이 측정값을 비용 함수 $J(w,b)$ 라고 한다. 훈련 중에는 모든 훈련 샘플 $x^{(i)}, y^{(i)}$ 에 대해 비용을 측정한다.

\[J(w,b) = \frac{1}{2m} \sum\limits_{i = 0}^{m-1} (f_{w,b}(x^{(i)}) - y^{(i)})^2\tag{2}\]

강의에서 경사하강법은 다음과 같이 표현할 수 있다.

\[\begin{align*} \text{repeat}&\text{ until convergence:} \; \lbrace \newline \; w &= w - \alpha \frac{\partial J(w,b)}{\partial w} \tag{3} \; \newline b &= b - \alpha \frac{\partial J(w,b)}{\partial b} \newline \rbrace \end{align*}\]

위에서 매개변수 $w$ 와 $b$ 가 동시에 업데이트 된다. gradient 는 다음과 같이 정의된다.

\[\begin{align} \frac{\partial J(w,b)}{\partial w} &= \frac{1}{m} \sum\limits_{i = 0}^{m-1} (f_{w,b}(x^{(i)}) - y^{(i)})x^{(i)} \tag{4}\\ \frac{\partial J(w,b)}{\partial b} &= \frac{1}{m} \sum\limits_{i = 0}^{m-1} (f_{w,b}(x^{(i)}) - y^{(i)}) \tag{5}\\ \end{align}\]

여기서 동시에(simultaneously) 라는 뜻은 모든 매개변수에 대한 편미분을 계산한 다음 어떤 매개변수도 업데이트 하지 않고 계산하는 것을 의미한다.

Implement Gradient Descent
one feature (한개의 특성)에 대한 경사하강 알고리즘을 구현해보자. 이를 위해 다음 세 가지 함수가 필요하다.
1. compute_gradient : 위의 (4)및 (5)번 방정식을 구현하는 함수이다.
2. compute_cost : 위의 (2)번 방정식을 구현하는 함수이다.
3. gradient_descent : compute_gradient 및 compute_cost 를 활용하는 함수이다.
Convex (관례)
파이썬 변수 이름에는 편미분을 포함한 컨벡스가 적용된다. 즉 $\frac{\partial J(w,b)}{\partial b}$ 는 dj_db 로 나타내게 된다.
“w.r.t” 는 “With Respect To” 의 약자로, $J(w,b)$ 의 $b$ 에 대한 편미분을 나타낸다.

compute_gradient
compute_gradient 는 (4)번 (5)번 방정식을 구현하고 $\frac{\partial J(w,b)}{\partial w}$,$\frac{\partial J(w,b)}{\partial b}$ 를 반환한다. 내부 주석은 수행되는 작업을 의미함.

  
def compute_gradient(x, y, w, b): 
    """
    Computes the gradient for linear regression 
    Args:
      x (ndarray (m,)): Data, m examples 
      y (ndarray (m,)): target values
      w,b (scalar)    : model parameters  
    Returns
      dj_dw (scalar): The gradient of the cost w.r.t. the parameters w
      dj_db (scalar): The gradient of the cost w.r.t. the parameter b     
     """
    
    # Number of training examples
    m = x.shape[0]    
    dj_dw = 0
    dj_db = 0
    
    for i in range(m):  
        f_wb = w * x[i] + b 
        dj_dw_i = (f_wb - y[i]) * x[i] 
        dj_db_i = f_wb - y[i] 
        dj_db += dj_db_i
        dj_dw += dj_dw_i 
    dj_dw = dj_dw / m 
    dj_db = dj_db / m 
        
    return dj_dw, dj_db

  
plt_gradients(x_train,y_train, compute_cost, compute_gradient)
plt.show()

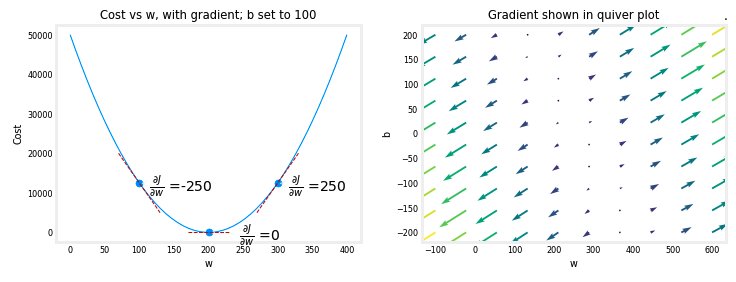
위의 왼쪽 그림은 세 지점에서의 cost curve 에 대한 기울기 또는 $\frac{\partial J(w,b)}{\partial w}$ 를 보여준다.
그림의 오른쪽 부분에서 기울기는 양수이고, 왼쪽에서는 음수이다. bowl shape 으로 인해 기울기는 항상 기울기가 0인 아래족으로 경사 하강을 이끌게 된다.
왼쪽 그림에서 $b = 100$ 이 고정 되어 있다. 경사 하강법은 $\frac{\partial J(w,b)}{\partial w}$ 및 $\frac{\partial J(w,b)}{\partial b}$ 를 모두 사용하여 매개 변수를 업데이트 한다.
위의 오른쪽 그림인 quiver plot 은 두 매개 변수의 기울기를 볼 수 있는 수단을 제공한다. 화살표의 크기는 해당 지점에서의 기울기의 크기를 반영한다. 화살표의 방향과 기울기는 해당 지점에서 $\frac{\partial J(w,b)}{\partial w}$ 와 $\frac{\partial J(w,b)}{\partial b}$ 의 비율을 반영한다.
기울기가 최소값에서 멀어지는 것을 살펴보자. 위의 방정식 (3)을 검토 필요함. 조정된 기울기가 현재 값에서 $w$ 또는 $b$ 를 뺀다. 이렇게 함으로 매개 변수를 비용을 줄일 방향으로 이동시킨다.

Gradient Descent
이제 기울기를 계산할 수 있으므로, 위의 방정식 (3)에서 설명한 경사 하강법을 아래의 gradient_descent 에 구현할 수 있다.
주석참조. 아래에서는 이 함수를 사용하여 훈련 데이터에서 $w$와 $b$의 최적값을 찾게 된다.

  
def gradient_descent(x, y, w_in, b_in, alpha, num_iters, cost_function, gradient_function): 
    """
    Performs gradient descent to fit w,b. Updates w,b by taking 
    num_iters gradient steps with learning rate alpha
    
    Args:
      x (ndarray (m,))  : Data, m examples 
      y (ndarray (m,))  : target values
      w_in,b_in (scalar): initial values of model parameters  
      alpha (float):     Learning rate
      num_iters (int):   number of iterations to run gradient descent
      cost_function:     function to call to produce cost
      gradient_function: function to call to produce gradient
      
    Returns:
      w (scalar): Updated value of parameter after running gradient descent
      b (scalar): Updated value of parameter after running gradient descent
      J_history (List): History of cost values
      p_history (list): History of parameters [w,b] 
      """
    
    # An array to store cost J and w's at each iteration primarily for graphing later
    J_history = []
    p_history = []
    b = b_in
    w = w_in
    
    for i in range(num_iters):
        # Calculate the gradient and update the parameters using gradient_function
        dj_dw, dj_db = gradient_function(x, y, w , b)     

        # Update Parameters using equation (3) above
        b = b - alpha * dj_db                            
        w = w - alpha * dj_dw                            

        # Save cost J at each iteration
        if i<100000:      # prevent resource exhaustion 
            J_history.append( cost_function(x, y, w , b))
            p_history.append([w,b])
        # Print cost every at intervals 10 times or as many iterations if < 10
        if i% math.ceil(num_iters/10) == 0:
            print(f"Iteration {i:4}: Cost {J_history[-1]:0.2e} ",
                  f"dj_dw: {dj_dw: 0.3e}, dj_db: {dj_db: 0.3e}  ",
                  f"w: {w: 0.3e}, b:{b: 0.5e}")
 
    return w, b, J_history, p_history #return w and J,w history for graphing

  
# initialize parameters
w_init = 0
b_init = 0
# some gradient descent settings
iterations = 10000
tmp_alpha = 1.0e-2
# run gradient descent
w_final, b_final, J_hist, p_hist = gradient_descent(x_train ,y_train, w_init, b_init, tmp_alpha, 
                                                    iterations, compute_cost, compute_gradient)
print(f"(w,b) found by gradient descent: ({w_final:8.4f},{b_final:8.4f})")

결과를 살펴보면 비용이 계속 감소하고있는것을 볼 수 있다. 또한 편미분값들도 점차적으로 감소한다.

Iteration    0: Cost 7.93e+04  dj_dw: -6.500e+02, dj_db: -4.000e+02   w:  6.500e+00, b: 4.00000e+00
Iteration 1000: Cost 3.41e+00  dj_dw: -3.712e-01, dj_db:  6.007e-01   w:  1.949e+02, b: 1.08228e+02
Iteration 2000: Cost 7.93e-01  dj_dw: -1.789e-01, dj_db:  2.895e-01   w:  1.975e+02, b: 1.03966e+02
Iteration 3000: Cost 1.84e-01  dj_dw: -8.625e-02, dj_db:  1.396e-01   w:  1.988e+02, b: 1.01912e+02
Iteration 4000: Cost 4.28e-02  dj_dw: -4.158e-02, dj_db:  6.727e-02   w:  1.994e+02, b: 1.00922e+02
Iteration 5000: Cost 9.95e-03  dj_dw: -2.004e-02, dj_db:  3.243e-02   w:  1.997e+02, b: 1.00444e+02
Iteration 6000: Cost 2.31e-03  dj_dw: -9.660e-03, dj_db:  1.563e-02   w:  1.999e+02, b: 1.00214e+02
Iteration 7000: Cost 5.37e-04  dj_dw: -4.657e-03, dj_db:  7.535e-03   w:  1.999e+02, b: 1.00103e+02
Iteration 8000: Cost 1.25e-04  dj_dw: -2.245e-03, dj_db:  3.632e-03   w:  2.000e+02, b: 1.00050e+02
Iteration 9000: Cost 2.90e-05  dj_dw: -1.082e-03, dj_db:  1.751e-03   w:  2.000e+02, b: 1.00024e+02
(w,b) found by gradient descent: (199.9929,100.0116)

출력된 경사 하강 과정의 몇 가지 특성에 대해 살펴보자.
1. 비용은 크게 시작하고 위 슬라이드에서 설명한 대로 빠르게 감소한다.
2. 편미분인 dj_dw 및 dj_db 도 처음에는 빠르게 감소하고 그 후 더 느리게 감소한다. 강의에서 설명했듯이 과정이 bottom of the bowl 에 가까워질수록 편미분의 값이 작아져 진행이 느려진다.
3. 학습률 $\alpha$ 는 고정된 채로 진행이 느려진다.

-Cost versus iterations of gradient descent

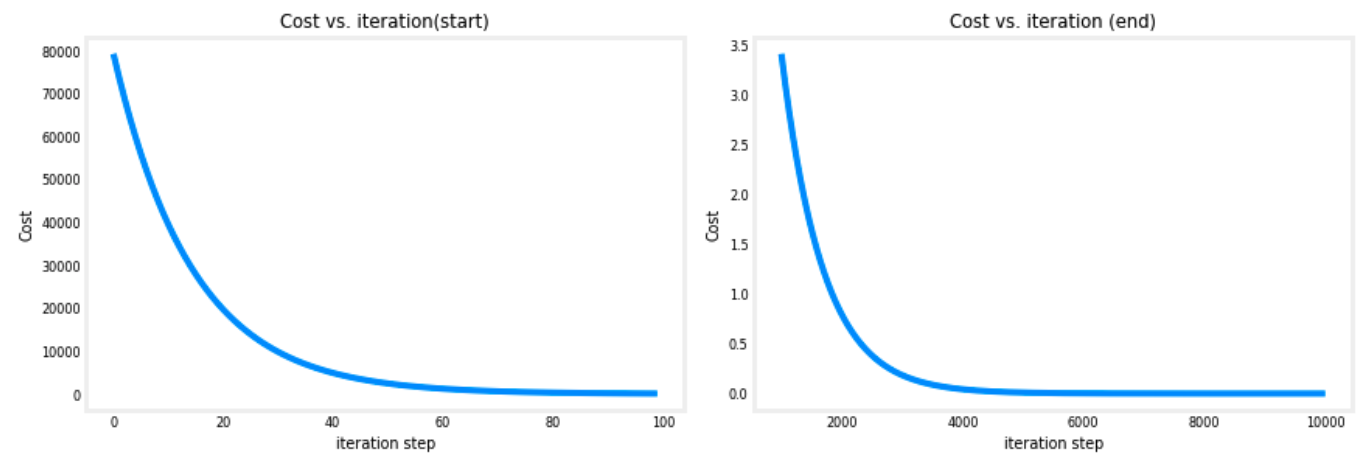
비용 대 반복 회수의 그래프는 경사 하강법 진행 상황을 측정하는 데 유용한 지표이다.
성공적인 실행에서는 비용이 항상 감소해야 한다.
비용 변화가 처음에 매우 빠르기 때문에, 초기 하강 과정을 최종 하강 과정과 다른 척도로 표시하는 것이 유용하다.
아래의 그래프에서는 비용과 반복 회수의 척도에 주의

  
# plot cost versus iteration  
fig, (ax1, ax2) = plt.subplots(1, 2, constrained_layout=True, figsize=(12,4))
ax1.plot(J_hist[:100])
ax2.plot(1000 + np.arange(len(J_hist[1000:])), J_hist[1000:])
ax1.set_title("Cost vs. iteration(start)");  ax2.set_title("Cost vs. iteration (end)")
ax1.set_ylabel('Cost')            ;  ax2.set_ylabel('Cost') 
ax1.set_xlabel('iteration step')  ;  ax2.set_xlabel('iteration step') 
plt.show()

Predictions
이제 매개변수 $w$와 $b$의 최적값을 발견했으므로, 모델을 사용하여 학습된 매개변수를 기반으로 주택 가치를 예측할 수 있다.
예상대로, 예측된 값은 동일한 주택에 대한 학습 값과 거의 동일하다. 그러므로, 예측에 포함되지 않은 값은 예상 값과 일치한다.

  
print(f"1000 sqft house prediction {w_final*1.0 + b_final:0.1f} Thousand dollars")
print(f"1200 sqft house prediction {w_final*1.2 + b_final:0.1f} Thousand dollars")
print(f"2000 sqft house prediction {w_final*2.0 + b_final:0.1f} Thousand dollars")

sqft house prediction 300.0 Thousand dollars
sqft house prediction 340.0 Thousand dollars
sqft house prediction 500.0 Thousand dollars

Plotting
경사 하강법 실행 중에 비용 함수의 변화를 보여주기 위해 cost(w,b)의 등고선 플롯에 iterations(반복 횟수)에 따른 cost(비용)을 플로팅할 수 있다.

  
fig, ax = plt.subplots(1,1, figsize=(12, 6))
plt_contour_wgrad(x_train, y_train, p_hist, ax)

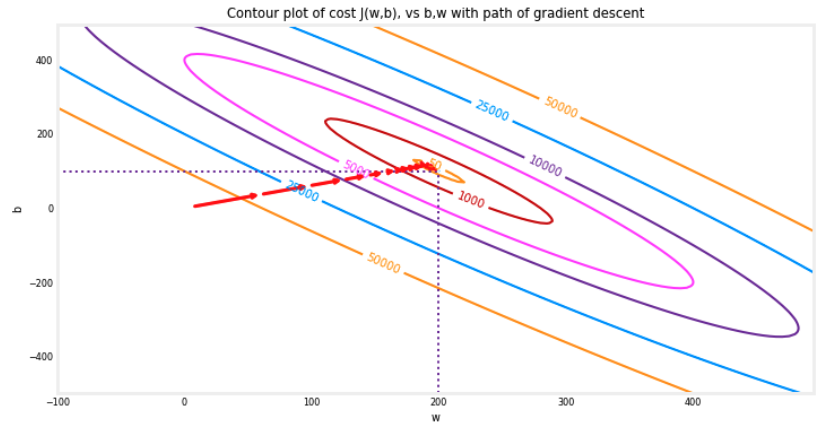
위의 등고선 플롯은 일정 범위의 $w$와 $b$에 대한 비용(cost(w,b))를 나타낸다. 비용 레벨은 등고선에서 원으로 표시된다.
빨간 화살표로 오버레이된 경사 하강법의 경로가 있다. 다음 사항에 유의하자.
1. 경로는 목표로의 꾸준한(단조적인) 진전을 보인다.
2. 초기 단계는 목표 지점에 가까워질수록 단계가 작아진다.
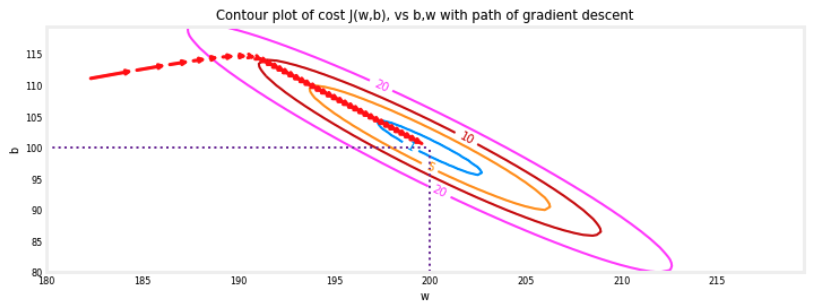
확대하여 볼 때, 경사 하강법의 최종 단계를 확인할 수 있다. 기울기가 0으로 접근할수록 각 단계 사이의 거리가 줄어든다는 점을 체크하자.

  
fig, ax = plt.subplots(1,1, figsize=(12, 4))
plt_contour_wgrad(x_train, y_train, p_hist, ax, w_range=[180, 220, 0.5], b_range=[80, 120, 0.5],
            contours=[1,5,10,20],resolution=0.5)

Increased Learning Rate
강의에서 방정식(3) 에서의 학습률 $\alpha$ 의 적절한 값에 대한 내용이 있었다. $\alpha$가 클수록 경사 하강법은 솔루션에 (converge)수렴하는 속도가 빨라졌었다.
하지만, 학습률이 너무 크면 경사 하강법이 diverge(발산)할 수 있다. 위의 등고선 플롯은 수렴이 잘되는 케이스였다.
이제 학습률 $\alpha$의 값을 증가시켜보고 그 결과를 살펴보자.

  
# initialize parameters
w_init = 0
b_init = 0
# set alpha to a large value
iterations = 10
tmp_alpha = 8.0e-1
# run gradient descent
w_final, b_final, J_hist, p_hist = gradient_descent(x_train ,y_train, w_init, b_init, tmp_alpha, 
                                                    iterations, compute_cost, compute_gradient)

Iteration    0: Cost 2.58e+05  dj_dw: -6.500e+02, dj_db: -4.000e+02   w:  5.200e+02, b: 3.20000e+02
Iteration    1: Cost 7.82e+05  dj_dw:  1.130e+03, dj_db:  7.000e+02   w: -3.840e+02, b:-2.40000e+02
Iteration    2: Cost 2.37e+06  dj_dw: -1.970e+03, dj_db: -1.216e+03   w:  1.192e+03, b: 7.32800e+02
Iteration    3: Cost 7.19e+06  dj_dw:  3.429e+03, dj_db:  2.121e+03   w: -1.551e+03, b:-9.63840e+02
Iteration    4: Cost 2.18e+07  dj_dw: -5.974e+03, dj_db: -3.691e+03   w:  3.228e+03, b: 1.98886e+03
Iteration    5: Cost 6.62e+07  dj_dw:  1.040e+04, dj_db:  6.431e+03   w: -5.095e+03, b:-3.15579e+03
Iteration    6: Cost 2.01e+08  dj_dw: -1.812e+04, dj_db: -1.120e+04   w:  9.402e+03, b: 5.80237e+03
Iteration    7: Cost 6.09e+08  dj_dw:  3.156e+04, dj_db:  1.950e+04   w: -1.584e+04, b:-9.80139e+03
Iteration    8: Cost 1.85e+09  dj_dw: -5.496e+04, dj_db: -3.397e+04   w:  2.813e+04, b: 1.73730e+04
Iteration    9: Cost 5.60e+09  dj_dw:  9.572e+04, dj_db:  5.916e+04   w: -4.845e+04, b:-2.99567e+04

위에서 $w$와 $b$가 양수와 음수 사이를 왔다갔다하면서 절대값이 각 반복마다 증가하는 것을 확인할 수 있다.
심지어 각 반복에서 $\frac{\partial J(w,b)}{\partial w}$ 가 부호를 바꾸며 비용이 감소하는 대신 증가하는 것을 확인할 수 있다.
이는 학습률이 너무 크고 솔루션이 발산하고 있다는 명백한 신호이다. 이를 플롯으로 시각화 해보면 다음과 같다.

  
plt_divergence(p_hist, J_hist,x_train, y_train)
plt.show()

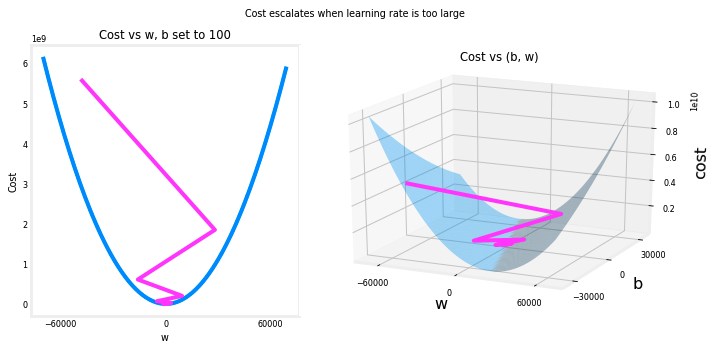
위의 왼쪽 그래프는 경사 하강법의 처음 몇 단계에서의 $w$ 의 진전을 보여준다.
$w$ 는 양수에서 음수로 진동하며 비용이 빠르게 증가한다..
경사 하강법은 $w$ 와 $b$ 둘 다 작용하므로 전체적인 그림을 파악하기 위해 오른쪽 3차원 플롯이 필요하다.