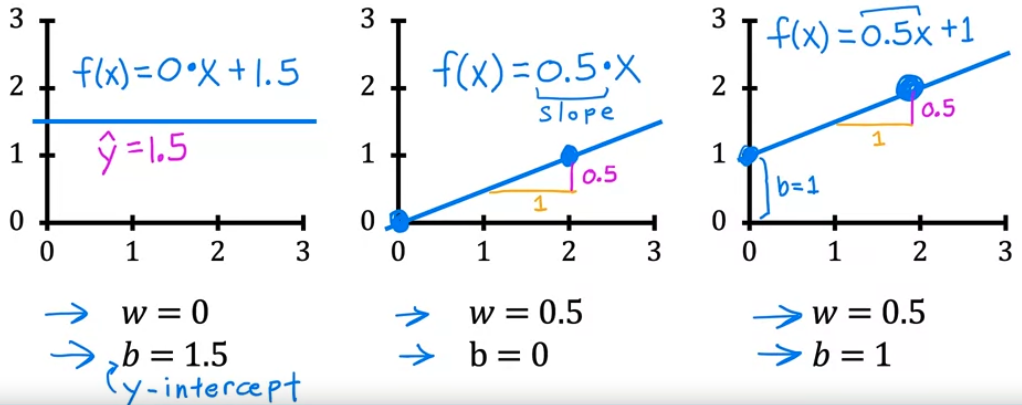Machine Learning - Cost Function

해당 포스트는 Andrew Ng 교수님의 Machine Learning Specialization 특화 과정에 대한 정리 내용을 참고하였습니다.

Cost function formula - 비용 함수 공식

linear regression (선형 회귀)를 구현하기 위한 첫 번째 핵심 단계는 먼저 cost function (비용 함수)를 정의하는 것이다. 비용 함수를 통해 모델의 학습을 더 잘 수행할 수 있다.
우리는 앞의 linear regression 의 모델이 선형 방정식임을 배웠다.

\[\large{f_{w,b}(x) = wx + b}\]

여기서 $w, b$ 가 뜻하는 바는 coefficients(계수), weights(가중치) 를 뜻한다.
그렇다면 $w, b$ 는 어떤 역할을 하는 것일까?

우리가 배웠던 직선 방정식을 떠올려보면 기울기(w)와 y절편(b)이 있으면 직선임을 직관적으로 이해할 수 있다.

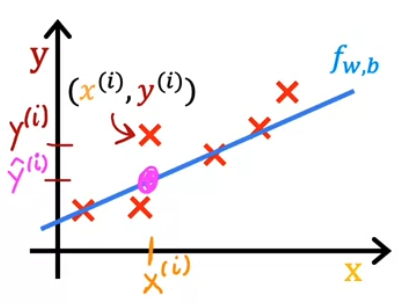
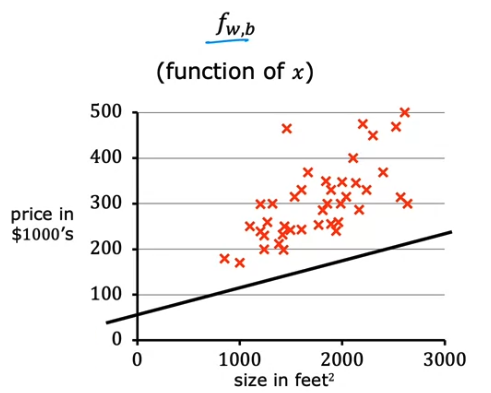
그렇다면, 다음 그림 처럼 임의의 training set 가 존재하고, 선형 회귀 분석을 했을 때 $f_{w,b}$ 직선이 training example 과 거의 비슷하거나 가까운 곳에 있다라고 생각할 수 있다.

$i^{th}$ 훈련 예제가 $(x^{(i)}, y^{(i)})$ 라고 했을 때
입력값 $x^{(i)}$ 에 대응되는 실제 목표값은 $y^{(i)}$ 이고 예측값은 $\hat{y}^{(i)}$ 임을 확인할 수 있다.
따라서 다음 식이 성립한다.

\[\hat{y}^{(i)} = f_{w,b}(x^{(i)})\] \[f_{w,b}(x^{(i)}) = wx^{(i)} + b\]

\[\large{\mbox{Find} \; w,b \; : \; \hat{y}^{(i)} \; \mbox{is close to } \; {y^{(i)}} \; \mbox{for all} \; (x^{(i)}, y^{(i)})}\]

우리는 여기서 모든 훈련 예제에서 $i$ 의 예측값인 $\hat{y}^{(i)}$ 이 실제 목표 $y^{(i)}$ 에 가깝게 하는 $w$ 와 $b$ 의 값을 찾아내야한다.
먼저 이 방법을 찾기 위해서는 직선이 훈련 데이터에 얼마나 잘 맞는지 측정하는 방법을 알아야한다. 이를 위해 cost function 을 생성해야한다.

cost function 은 $\hat{y} - y$ 즉 error(오차)를 구하고 예측값이 목표값으로부터 얼마나 멀리 떨어져 있는지를 측정한다.
그리고, i = 1 부터 m 까지 모든 훈련 예제의 squared error (오차의 제곱)을 구한 뒤 관례에 따라 training set 의 크기가 커져도 자동으로 커지지 않는 cost function 을 만들기 위해서
Mean Squared Error (평균 제곱 오차)를 계산한다. (m 으로 나눔)
추가적으로 cost function 의 편도함수를 찾을 때 수학적 편의를 위해 2를 나눠주면 다음 공식이 성립한다.
참고로 이 식을 단변량 MSE (Mean Squared Error) 라고 한다.
\[\large{J(w,b) = \frac{1}{2m} \sum\limits_{i = 1}^{m} (\hat{y}^{(i)} - y^{(i)})^2 \tag{1}}\]

위에서 $\hat{y}^{(i)} = f_{w,b}(x^{(i)})$ 이므로 다음과 같이 변형이 가능하다.
\[\large{J(w,b) = \frac{1}{2m} \sum\limits_{i = 1}^{m} (f_{w,b}(x^{(i)}) - y^{(i)})^2 \tag{2}}\]

응용 분야마다 다른 cost function 을 사용하지만, MSE 는 단연코 linear regression 에서 가장 일반적으로 사용되는 함수이다.
결국 우리는 cost function $J(w,b)$ 를 작게 만드는 $w, b$ 값을 찾아야한다.
goal : $\underset{w,b}{\mbox{minimize}} \; J(w,b)$

Cost function intuition - 비용 함수 직관

cost function $J$ 의 목표인 $\underset{w,b}{\mbox{minimize}} \; J(w,b) \quad$ 를 찾기 위해서 우리는 선형 회귀 모델을 좀 더 simplified (단순화)된 버전으로 만들어야 한다.

$b = 0$ 인 경우

즉, $w$ 만 사용하여 비용 함수의 최소값을 구해보는 과정이다.
매개변수 b 를 제거하거나 0으로 만들어 보면 다음과 같다.

\[\large{f_w (x) = wx } \quad , \quad b = 0\]

\[\large{J(w) = \frac{1}{2m} \sum\limits_{i = 1}^{m} (f_w(x^{(i)}) - y^{(i)})^2 }\]

$f_w(x^{(i)})$ 는 $wx^{(i)}$ 로 표현할 수 있다.

\[= \frac{1}{2m} \sum\limits_{i = 1}^{m} (wx^{(i)} - y^{(i)})^2\]

이 단순화된 모델의 목표는 cost function $J$ 를 최소화하는 $w$ 를 찾는 것이다.

\[\large{\underset{w}{\mbox{minimize}}} \; J(w)\]

매개변수 $w$ 에 대해 서로 다른 값을 선택할 때 cost function 이 어떻게 변하는지 살펴보자.
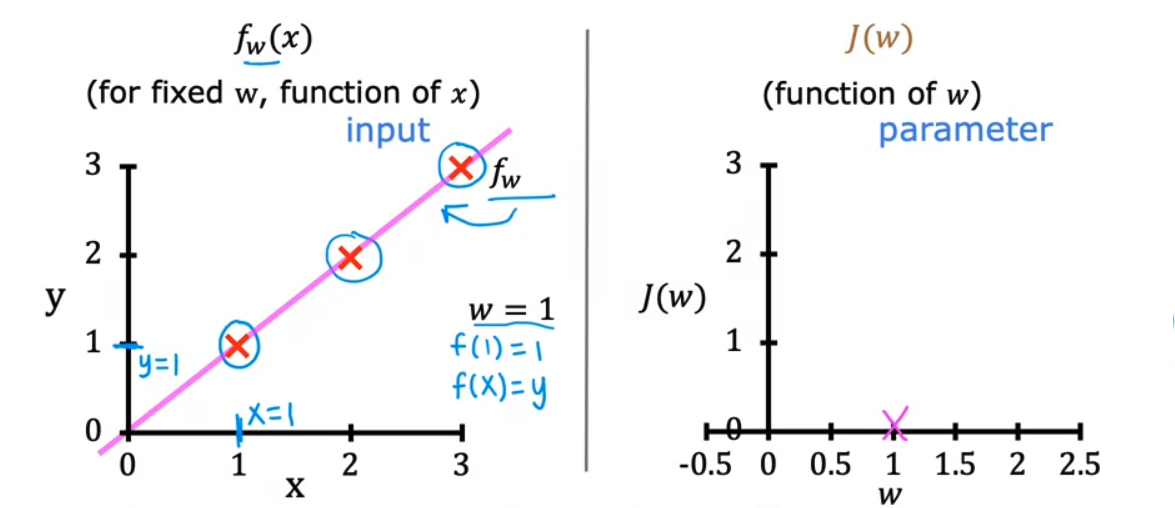
특히 $f_w (x)$ 모델과 $J(w)$ 비용 함수의 그래프를 살펴보자.

$w = 1$ 인 경우

$J(1) = \frac{1}{2m} \sum\limits_{i = 1}^{m} (f_w(x^{(i)}) - y^{(i)})^2 = \frac{1}{2m} \sum\limits_{i = 1}^{m} (wx^{(i)} - y^{(i)})^2 = \frac{1}{2m} (0^2 + 0^2 + 0^2) = 0$ 이므로 $J(w)$ 에 플롯되는 값은 0이다.

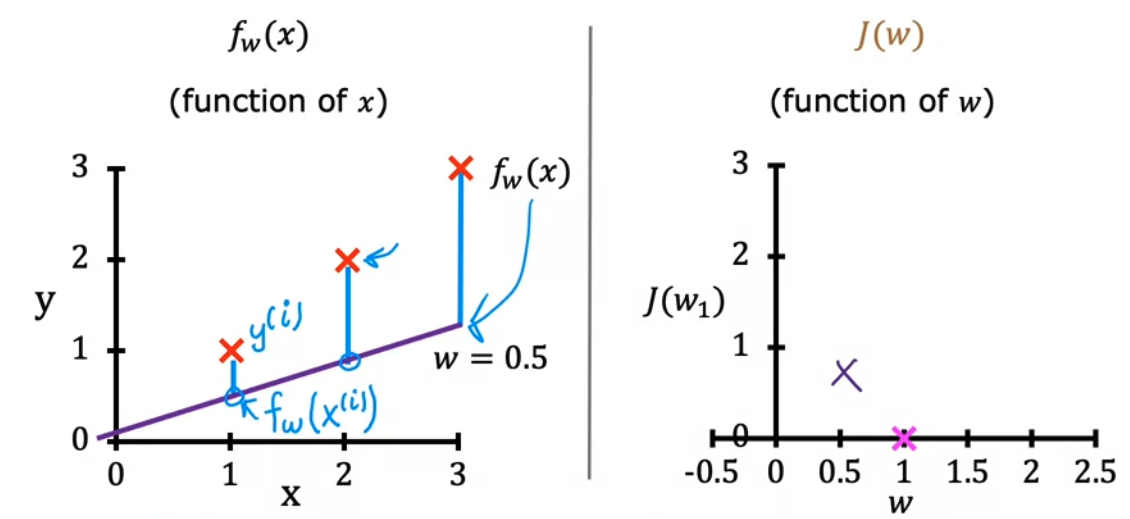
다음은 $w = 0.5$ 인 경우를 살펴보자

$w = 0.5$ 인 경우

$J(0.5) = \frac{1}{2m} [ ((0.5 \times 1) - 1)^2 + ((0.5 \times 2) - 2)^2 + ((0.5 \times 3) - 3)^2 ] = [ (0.5 - 1)^2 + (1 - 2)^2 + (1.5 - 3)^2 ] = \frac{1}{2 \times 3} [3.5] = \frac{3.5}{6} \approx 0.58$ 가 된다.

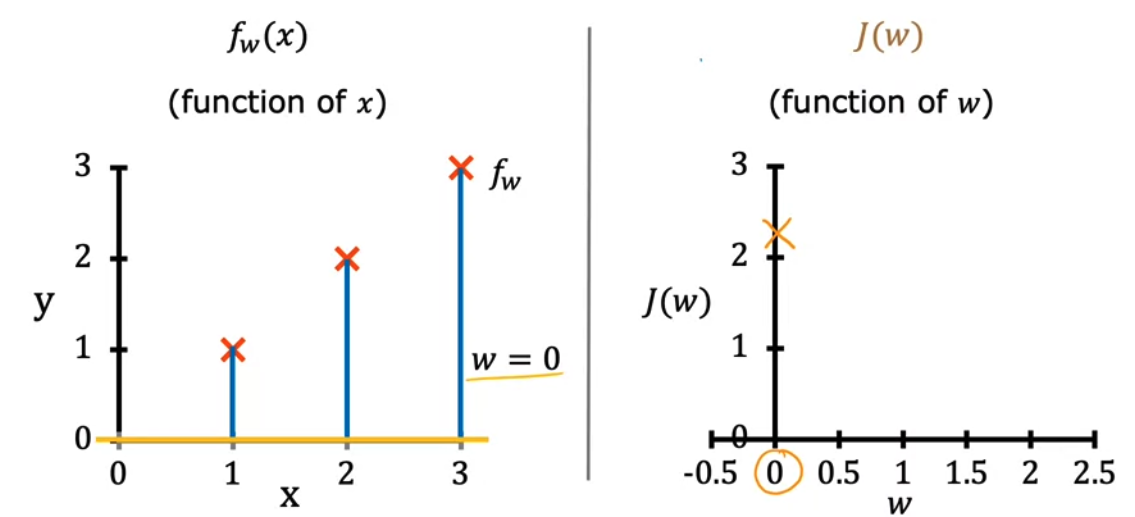
그리고 $w = 0$ 인 경우는

$w = 0$ 인 경우

$J(0) = \frac{1}{2m} (1^2 + 2^2 + 3^2) = \frac{1}{6} [14] \approx 2.3$ 가 된다. 이후 점점 $w$ 값을 계속해서 바꿔나가면 비용 함수 $J(x)$ 의 그래프는 다음과 같이 그릴 수 있다.

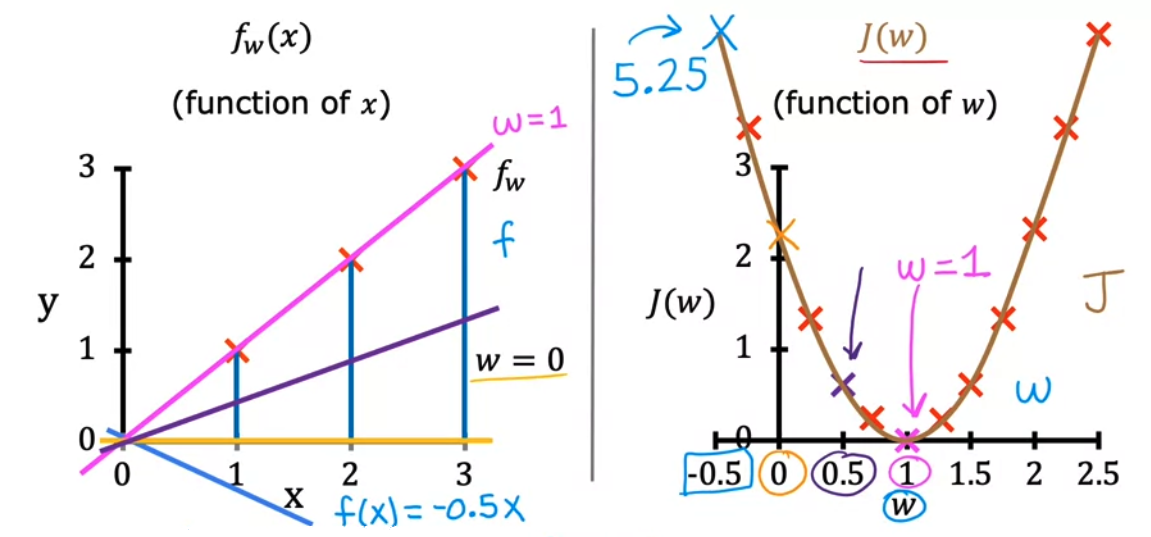
위 그림에서 어떤 $w$ 값을 고르면 될까? 우리는 비용 함수 $J(x)$ 가 가장 최솟값이 되는 부분을 찾으면 된다. 이차함수의 경우 vertex (변곡점) 이므로 $w = 1$ 이 가장 최소값이 될 것이다.
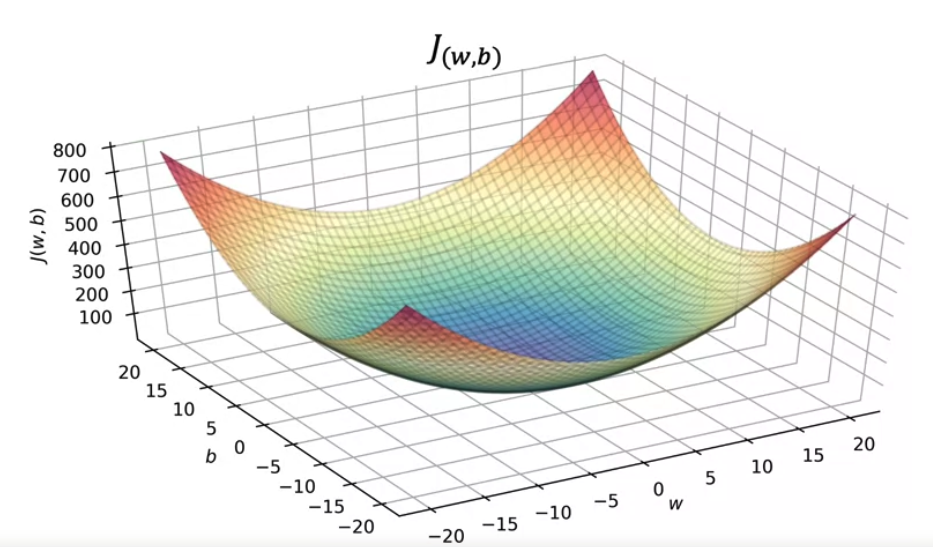
다음은 매개변수 $w, b$ 두 개를 사용하여 비용 함수 $J$ 를 시각화 해보자.

function of $x$

$f_{w,b} (x) = 0.06x + 50$ 이라고 가정했을 때 $w, b$ 두 개의 매개변수가 있기 때문에, 비용 함수 $J$ 의 그래프는 3차원으로 확장된다.

function of $w,b$

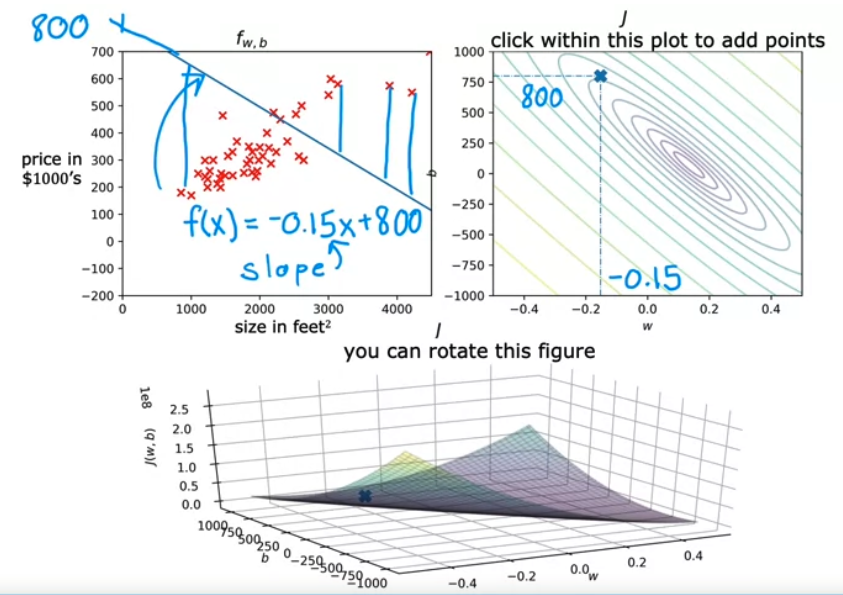
비용 함수를 등고선도로 시각화하여 살펴보면 다음과 같다.

임의의 직선을 하나 그은 뒤 등고선에 대응되는 점을 찾는다.
등고선의 높이가 커지는 부분일 수록 비용 함수의 크기가 작아진다.
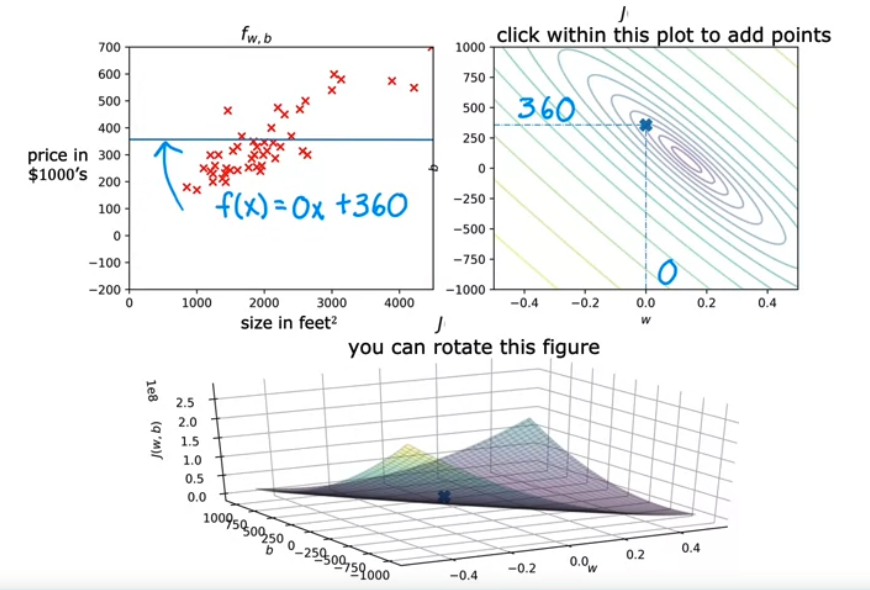
그리고 점점 매개변수를 바꿔가면

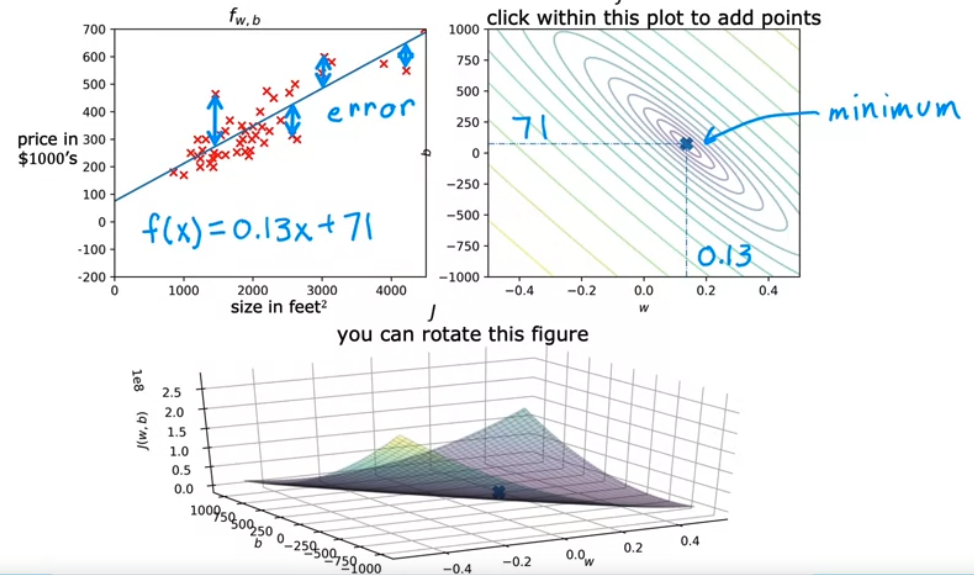
minimum 이 되는 지점을 찾을 수 있다.

실습

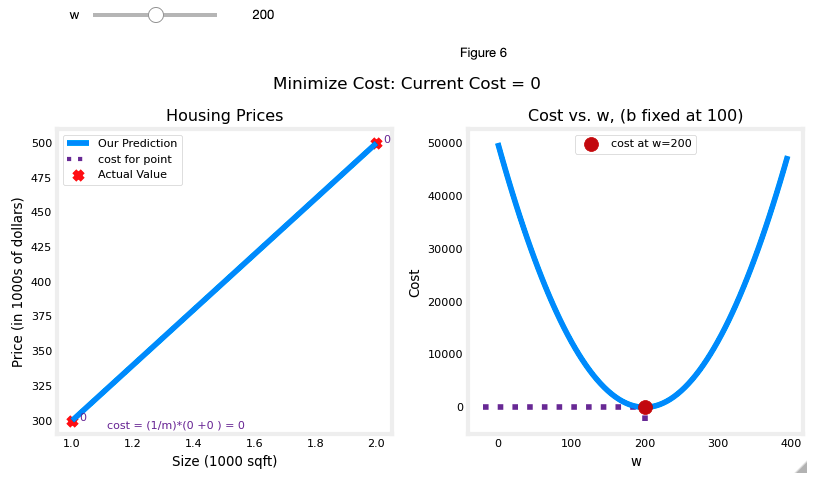
Simplified Cost Function Visualization
주의, plt_intuition, plt_stationary, plt_update_onclick, soup_bowl 함수들은 코세라 강의 오픈랩에서만 사용가능함

Problem Statement
집의 크기를 고려하여 주택 가격을 예측할 수 있는 모델을 원한다고 하자.
1000 sqft 가 30만 달러에 판매된 집과 2000 sqft 가 50만 달러에 판매된 집이 있다고 하자.

Size (1000 sqft)	Price (1000s of dollars)
1	300
2	500

  
x_train = np.array([1.0, 2.0])           #(size in 1000 square feet)
y_train = np.array([300.0, 500.0])           #(price in 1000s of dollars)

def compute_cost(x, y, w, b): 
    """
    Computes the cost function for linear regression.
    
    Args:
      x (ndarray (m,)): Data, m examples 
      y (ndarray (m,)): target values
      w,b (scalar)    : model parameters  
    
    Returns
        total_cost (float): The cost of using w,b as the parameters for linear regression
               to fit the data points in x and y
    """
    # number of training examples
    m = x.shape[0] 
    
    cost_sum = 0 
    for i in range(m): 
        f_wb = w * x[i] + b   
        cost = (f_wb - y[i]) ** 2  
        cost_sum = cost_sum + cost  
    total_cost = (1 / (2 * m)) * cost_sum  

    return total_cost

plt_intuition(x_train,y_train)

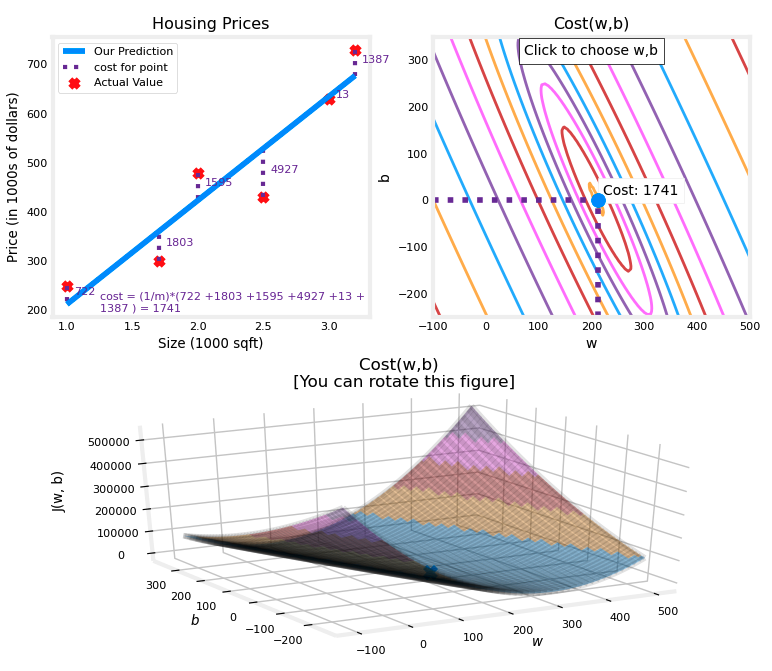
Cost Function Visualization - 3D

  
x_train = np.array([1.0, 1.7, 2.0, 2.5, 3.0, 3.2])
y_train = np.array([250, 300, 480,  430,   630, 730,])

plt.close('all') 
fig, ax, dyn_items = plt_stationary(x_train, y_train)
updater = plt_update_onclick(fig, ax, x_train, y_train, dyn_items)

minimum 값인 경우

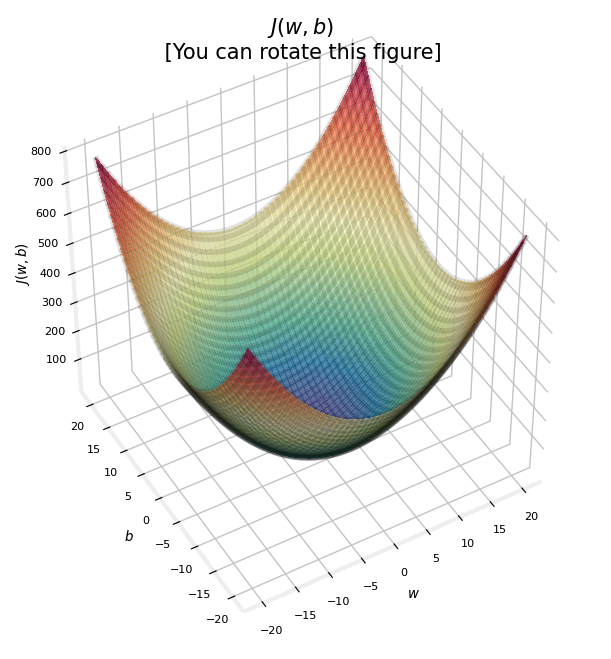
Convex Cost Surface
비용 함수가 error 를 제곱한다는 사실은 erros surface 가 수프 그릇 처럼 볼록하다는 것을 의미한다.
선형대수학에서 배웠던 것 중 quadratic form 에서 positive definite 과 유사한 생김새이다..

Machine Learning - Cost Function

목차

Cost function formula - 비용 함수 공식

Cost function intuition - 비용 함수 직관

실습

Trending Tags