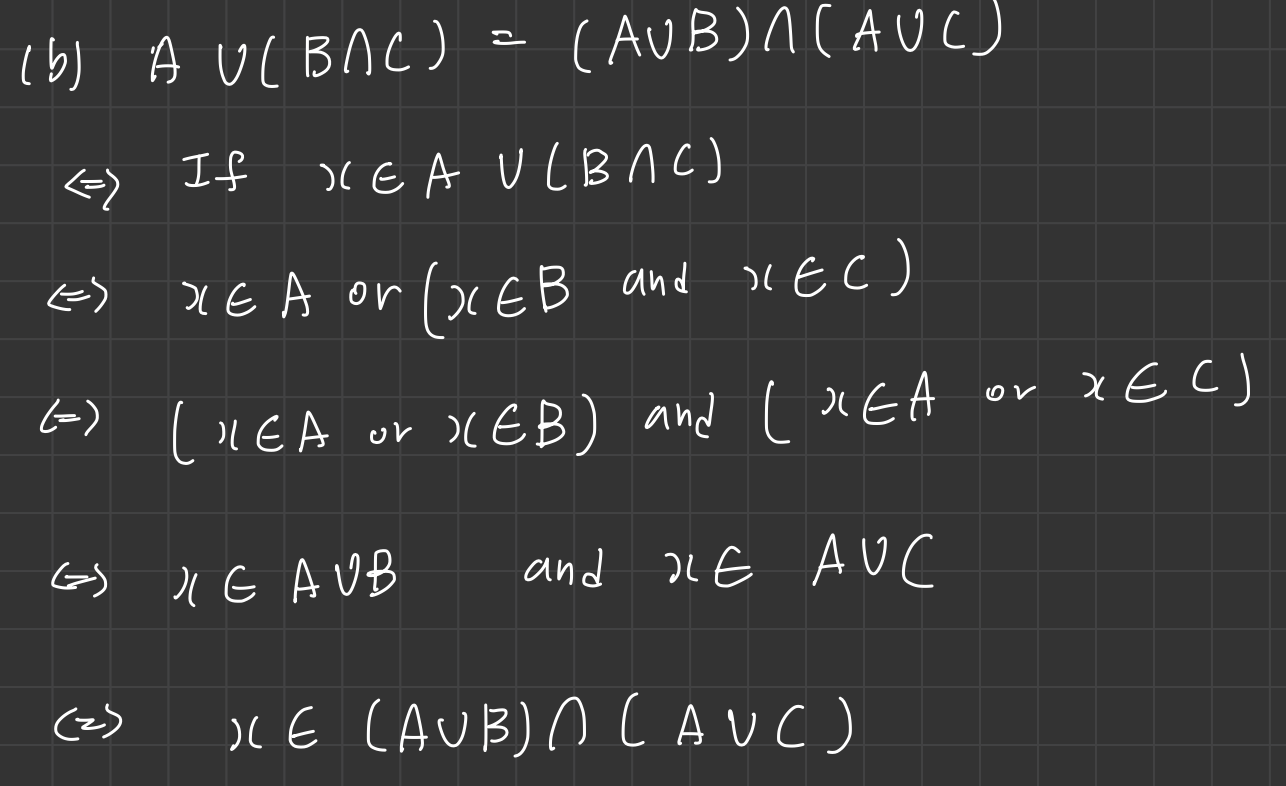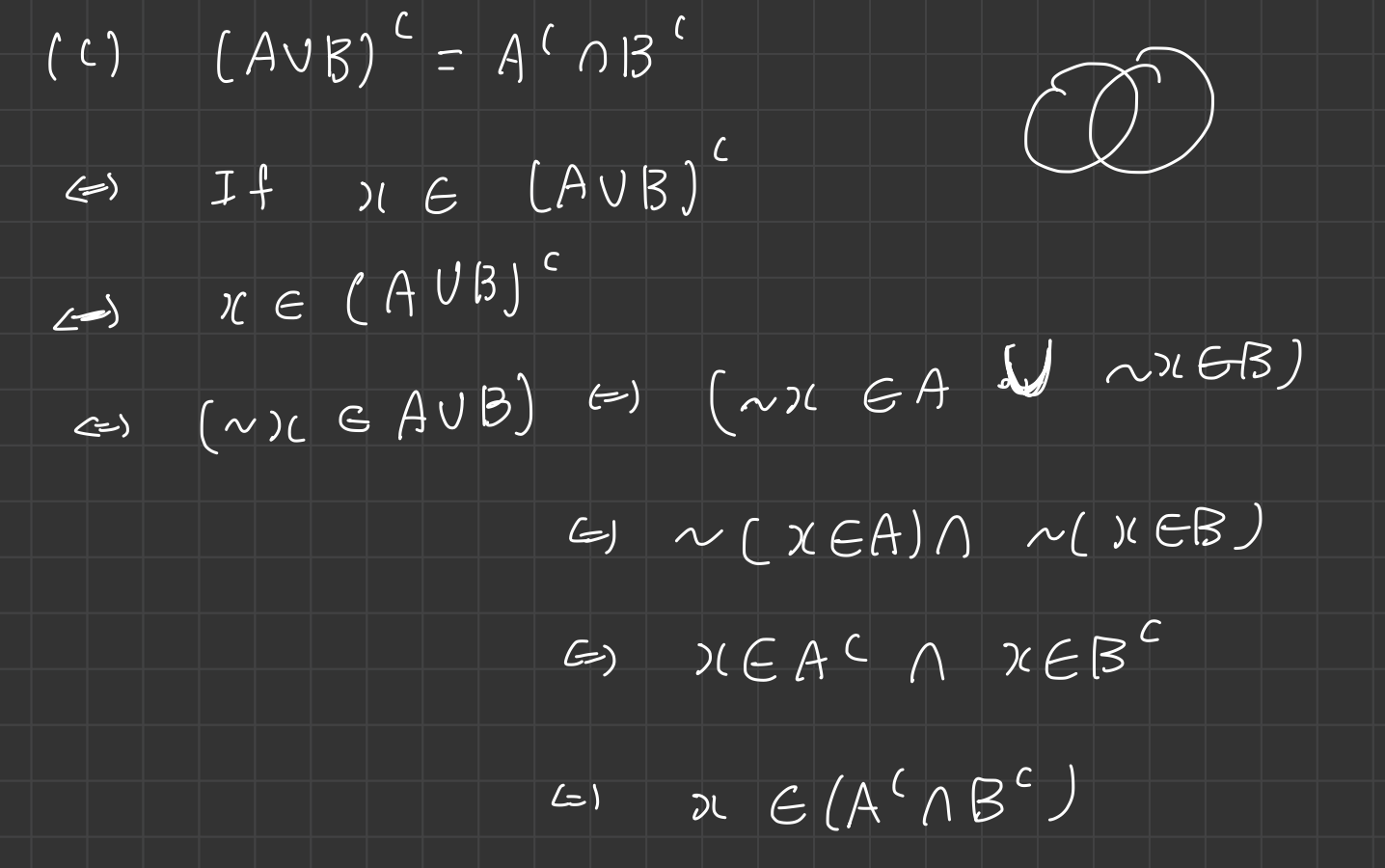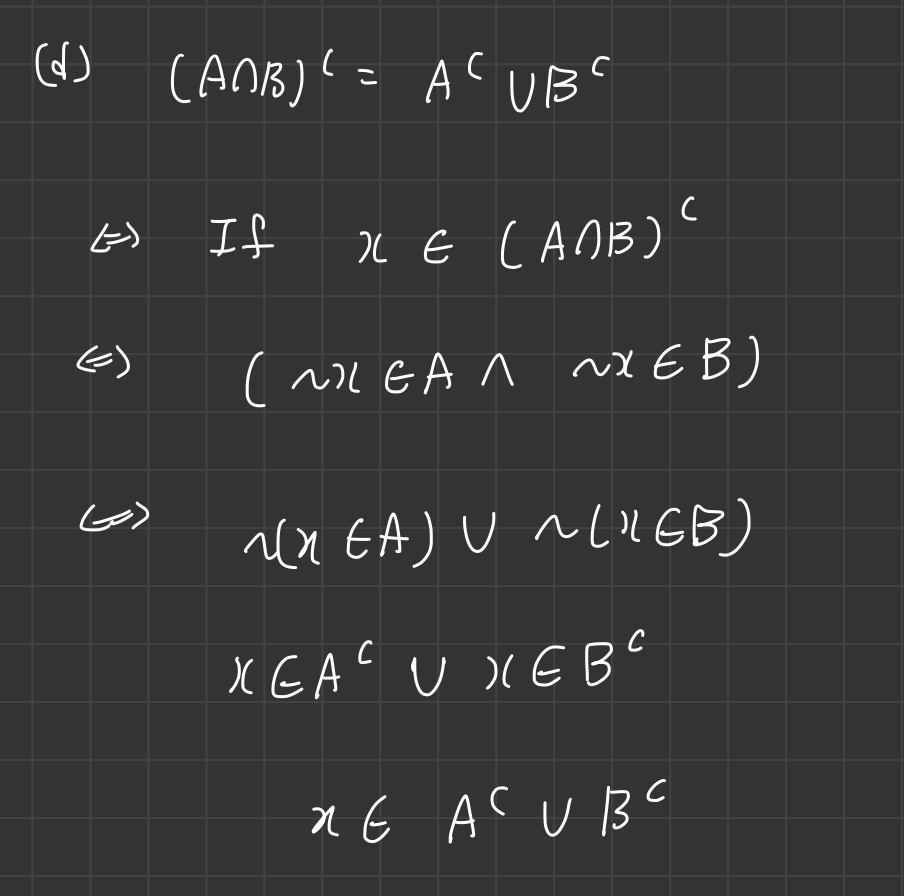Set Theory - 1. Basis of Set Theory
용어 정리
- Set = Collection (집합) =? Family (집합족)
- Power of Set (멱집합)
- Rational Number (유리수), Irrational Number (무리수)
- $ := $ (~로 정의하다 라는 수식)
- Proposition (증명이 된 명제, theorem 보단 그 의미가 약하다.)
- Q.E.D (Quad Erat Demonstrandum) - 증명 완료라는 라틴어
- domain (정의역), codomain (공역), Im$f$ = image (치역, 상), reverse image (역상)
Set Theory - 집합론
- Set = Collection 로 부를 수 있다. =? Family 는 집합족이라고한다..
- {definable objects} - “기준”(True/False)이 제시된 대상들의 모임을 집합(Set)이라고 한다.
ex. 키가 170 이상인 사람들의 모임 (집합)
ex. 잘생긴 사람들의 모임 (집합이 아님)
Notation - 표기법
\[A = \{ -1, 2, 4, 5 \}, \; -1 \in A , \quad 0 \notin A\]- -1 은 집합 A의 원소이다. 0은 집합 A의 원소가 아니다.
- Set Builder Notation - 조건 제시법
- 집합은 $x$ 들을 모아놓은 것인고 그 $x$ 가 만족해야하는 조건은 $ \mathcal{P}(x) $ 이라는 것을 조건 제시법이라고 한다.
- 이 형식으로 집합을 정의한다. 원소는 꼭 숫자일 필요는 없다.
집합의 예시
자연수 Set of Natural Number
\(\mathbb{N} = \{ 1, 2, 3, 4, \dots \}\)정수 Set of Integer Number
\(\mathbb{Z} = \{ 1, 2, 3, 4, 0 , -1, -2, -3, \dots \}\)유리수 Set of Rational Number <-> 무리수 Irrational Number
\(\mathbb{Q} = \{ {q \over p} \mid p, q \in \mathbb{Z}, q \ne 0 \}\)실수 Set of Real Number
\(\mathbb{R} = \{ real S \}\)복소수 Set of Complex Number
\(\mathbb{C} = \{ complex S \}\)실수와 복소수는 뒷장에서 자세히 파헤쳐보자.. 링크 삽입 요망
Universial Set - 전체 집합
Def.
Let $X$ is universial set and $ A, B \subseteq X $
\(A \cup B \:= \{ x \mid x \in A \quad or \quad x \in B \}\)
\(A \cap B \:= \{ x \mid x \in A \quad and \quad x \in B \}\)
\(A^c \:= \{ x \mid x \notin A \}\)
Def.
if $ A, B \subseteq X $ , Define $ A = B $
$ \Leftrightarrow $ If $ x \in A $ , then $ x \in B $ ,
$ \Leftrightarrow $ and if $ y \in B $ , then $ y \in A $ .
증명
Proposition.
Let $A, B, C \subseteq X$ .a. $ A \cap (B \cup C) \overset{\underset{\mathrm{?}}{}}{=} (A \cap B) \cup (A \cap C) $
Proof.
Need to show (NTS) : $ A \cap (B \cup C) \; \subset \; (A \cap B) \cup (A \cap C) $
and $ (A \cap B) \cup (A \cap C) \; \subset \; A \cap (B \cup C) $
$ \Leftrightarrow $ If $x \in A \cap (B \cup C)$
$ \Leftrightarrow $ $ x \in A $ and ($x \in B $ or $ x \in C $)
$ \Leftrightarrow $ ($x \in A$ and $x \in B$) or ($x \in A$ and $x \in C$)
$ \Leftrightarrow $ $x \in A \cap B $ or $ x \in A \cap C $
$ \Leftrightarrow $ $x \in (A \cap B) \cup (A \cap C) $ Q.E.D $\blacksquare$
Power Set - 멱집합
\[C = \{ 1, 2 \}\] \[\mathcal{P}(C) = \{ \varnothing , \{ 1 \}, \{ 2 \} \{ 1, 2 \} \}\]- 멱집합은 집합의 집합 즉, set of collection, power set of C 이라고도 부르며 집합 C 의 모든 부분집합들의 모임을 의미한다.
- 멱집합은 $2^A$ 로 나타낼 수 있으며, \(A = \{ 1, 2 \}\) 일 때, \(2^A = \{ \varnothing, \{ 1 \}, \{ 2 \}, \{ 1, 2 \} \}\) 이다.
- 참고로 n개의 원소를 갖는 집합 A 에 대하여 A 의 부분집합들의 개수는 $2^n$ 이다.
- 멱집합의 정의..
Def. power set definition
Given a set $A$ ,
\(\mathcal{P}(A) := \{ B \subset A \}\) . the collection of subsets of $A$ called the power set of $A$ .
- 멱집합 개수의 증명
If $A$ has $n$ elements, then show that $\mathcal{P}(A)$ has $2^n$ elements.
Prrof.
몰?루 나중에 추가할 예정..
- 곱집합의 정의..
Def. product set definition
Given two sets $A, B$ ,
\(A \times B = \{ (a,b) \mid a \in A \, , \, b \in B \}\)
Functions - 함수
Def.
Given two sets $A, B$ ,
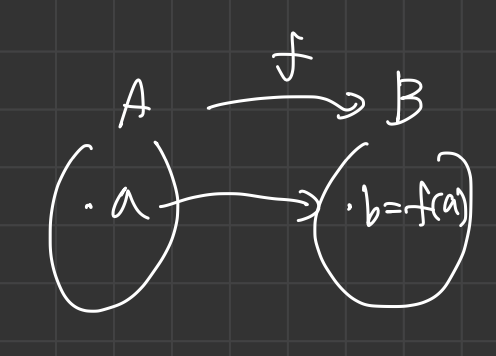
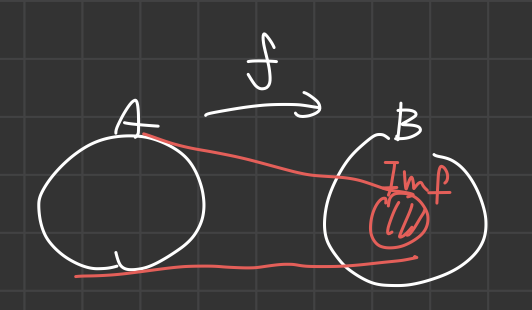
We call $ f : A \longrightarrow B $ is a function,
if we have $ S_f \subseteq A \times B $ satisfying for each $ a \in A $ , there exists $ b \in B $ uniquely such that $ (a,b) \in S_f $ .
- A 의 원소들 하나하나가 유일하게 B의 원소들에 대응된다.
- 여기서 우리는 A 를 domain (정의역), B 를 codomain (공역) 이라고 부른다.
the image of $f$, the range of $f$
Image of $f$ 즉, Im$f$ = \(\{ b = f(a) \mid a \in A \}\) 우리는 이것을 image (치역, 상) 이라고 한다.
Proposition2.
Given $ f : A \longrightarrow B $ a function,
Let $ A_1, A_2 \subseteq A $
\(f(A_1 \cup A_2) := \{ f(x) \mid x \in A_1 \cup A_2 \} = f(A_1) \cup f(A_2)\)$ f(A_1 \cap A_2) = f(A_1) \cap f(A_2) $
Proof.
추후 추가
Def.
Given $ f : A \longrightarrow B $ a function,
Let $B_1 \subseteq B$
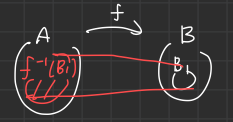
Define \(f^{-1}(B_1) := \{ x \in A \mid f(x) \in B_1 \}\)
Called the inverse image of $f$ under $ B_1 $ ($B_1$ 의 역상 이라고 부른다.)
Proposition3.
Let $ f : A \longrightarrow B $ a function, $B_1, B_2 \subset B$a. $f^{-1}(B_1 \cup B_2) = f^{-1}(B_1) \cup f^{-1}(B_2)$
b. $f^{-1}(B_1 \cap B_2) = f^{-1}(B_1) \cap f^{-1}(B_2)$
c. $f^{-1}({B_1}^c) = f^{-1}(B_1)^c$Proof.
추후 추가