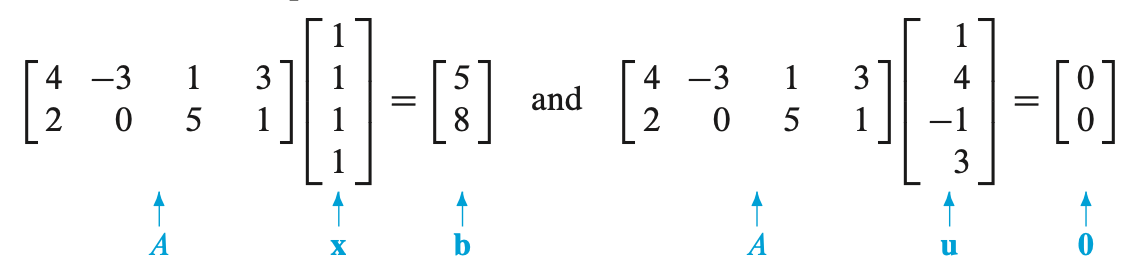Linear Algebra - 1.7 Introduction to Linear Transformation

용어 정리

• Matrix Multiplication (행렬 곱셈)
• Transformation (변환)
• matrix transformation (행렬 변환)
• linear transformation (선형 변환)

Matrix Multiplication - 행렬 곱셈

• x 가 A vector 에 의해 b 가 되었다.
• u 가 A vector 에 의해 0 이 되었다.

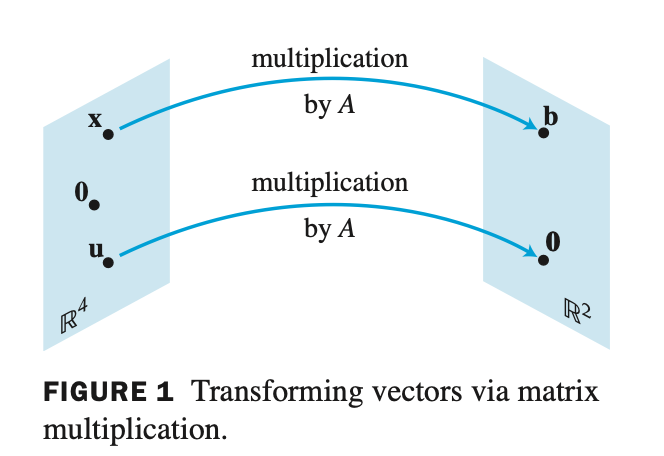
  벡터 x 는 $ \mathbb{R}^{4} $ 공간에 있다. 여기에 A matrix 를 곱한 b를 보면 $ \mathbb{R}^{2} $ 공간으로 이동한것을 확인할 수 있다. 이런 이동을 Transformation 이라 한다. 또는 function, mapping 이라고 말한다.

• A vector 가 $ \mathbb{R}^{4} $ space 에 있는 x vector를 $ \mathbb{R}^{2} $ space로 Transformation 시켰다.
• Transformation 은 이처럼 Matrix Multiplication에 의해 발생한다.

Transformation

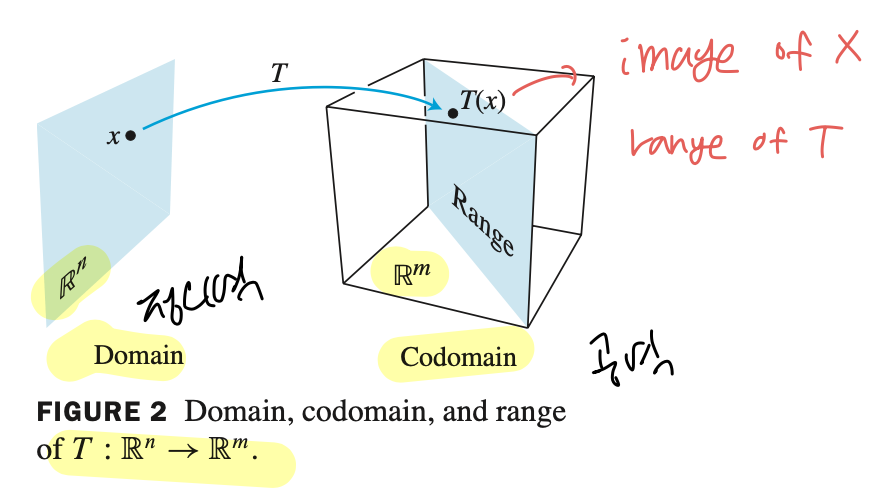
• $\mathbb{R}^{n}$ 에서 $ \mathbb{R}^{m}$ 로의 transformation (or function or mapping) $T$는 규칙이 있다.
• $ \mathbb{R}^{n}$ 에 있는 vector x를 $ \mathbb{R}^{n} $ 에 있는 $T(\mathrm{x})$ 로 할당하는 것이다. 이 규칙을 Transformation (변환) 이라한다.

• $\mathbb{R}^{n}$ 공간을 Domain (정의역)
• $\mathbb{R}^{m}$ 공간을 Codomain (공역) 이라 한다.

\[T : \mathbb{R}^{n} \rightarrow \mathbb{R}^{m}\]

• Transformation 은 위 기호처럼 나타낼 수 있다.
• 여기서 $T(\mathrm{x})$를 x의 image 라고 한다. image의 모든 set을 $T$의 range 라고 한다.

Matrix Transformation

• Matrix Transformation 은 $\mathbb{R}^{n}$ space 의 Domain 에 있는 x 를 $\mathbb{R}^{m}$ space의 Codomain으로 Transformation 하는 것이다.
• $\mathbb{R}^{n}$ space에 있는 x 에 대해서 $T(\mathrm{x})$ 는 $A\mathrm{x}$ 를 계산하는 것이다. 여기서 $A$는 $m \times n$ 행렬이다.
• 기호는 아래와 같이 표현 가능하다. (x 의 image 는 Ax가 된다.)

\[\mathrm{x} \mapsto A\mathrm{x}\] \[T : \mathbb{R}^{n} \rightarrow \mathbb{R}^{m}\]

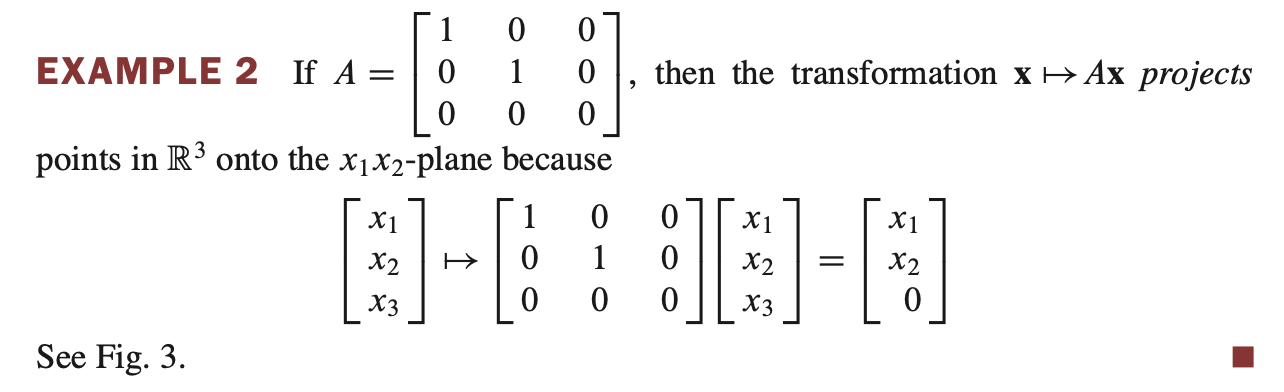
Transformation 예시

• 1번 예제

  

• matrix A로 x를 이동시키면 $x_3$ 는 모두 0이 되어서 공간에 있던 모든 점들이 한 면으로 모인다. (이를 projection 이라고 한다.)

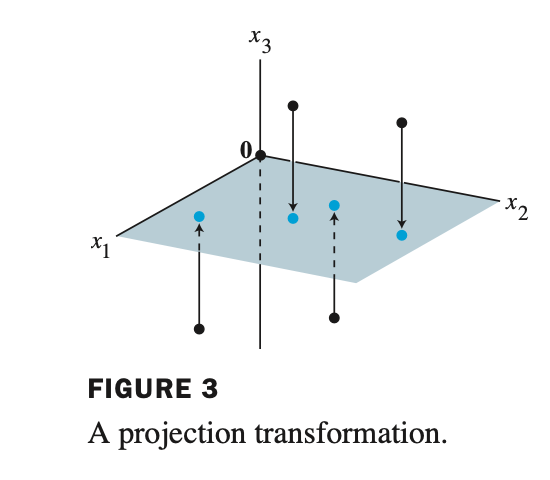
• 이를 기하학적으로 표현하면

  

• 3차원에 있는 임의의 vector에서 $x_3$ 에 해당하는 value가 zero가 되었다. 따라서 Span {$ x_1, x_2 $} 평면으로 표현된다.

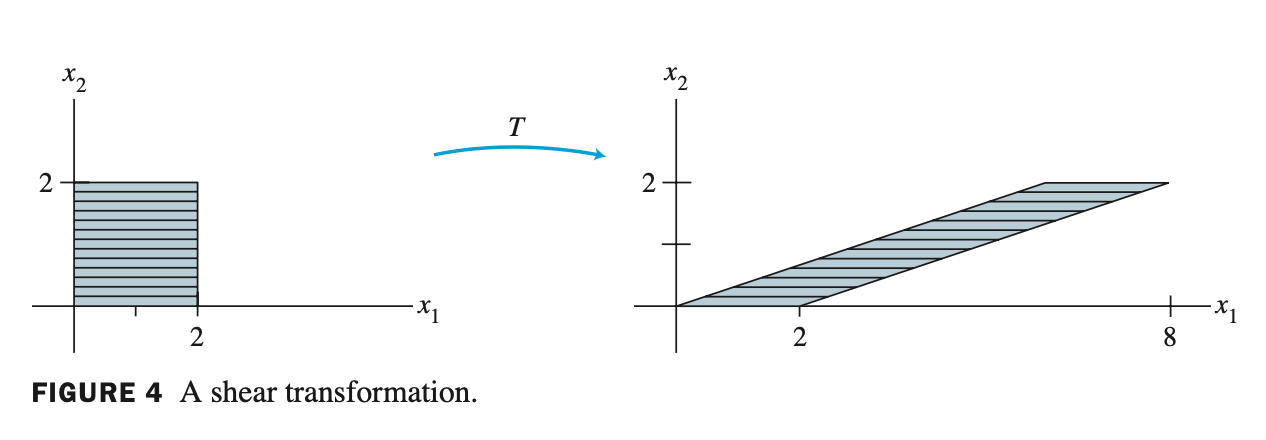
• 2번 예제

\[A = \begin{bmatrix} 1 & 3 \\\ 0 & 1 \; \end{bmatrix}\] \[\mathbf{u} = \begin{bmatrix} 0 \\\ 2 \; \end{bmatrix}\] \[T(\mathbf{u}) = \begin{bmatrix} 1 & 3 \\\ 0 & 1 \; \end{bmatrix} \, \begin{bmatrix} 0 \\\ 2 \; \end{bmatrix} = \begin{bmatrix} 6 \\\ 2 \; \end{bmatrix}\] \[the \quad image \quad of \; \begin{bmatrix} 2 \\\ 2 \; \end{bmatrix} \; is \; \begin{bmatrix} 1 & 3 \\\ 0 & 1 \; \end{bmatrix} \; \begin{bmatrix} 2 \\\ 2 \; \end{bmatrix} = \begin{bmatrix} 8 \\\ 2 \; \end{bmatrix}\]

• 이런 transformation을 shear transformation 이라고도 한다.

Linear Transformation - 선형 변환

• Transformation 이 Linear Transformation 이라고 불릴 조건에 대해서 알아보자.

  

• 이 두 가지 조건을 만족하는 Transformation 은 Linear Transformation이다.

  이는 Theorem 5 와 동일하다!! matrix equation 은 linear system 이고 이것은 위 두 조건을 성립한다고 배웠다. 마찬가지로 위 두 조건을 만족하면 transformation 도 linear로 정의가 가능하다.

• $m \times n$ matrix 가 Theorem5 성질을 지니고 있으므로 모든 matrix transformation 은 linear transformation이다. linear transformation 이 아닌 trnasformation이 있지만, matrix transformation은 linear transformation이다.

  

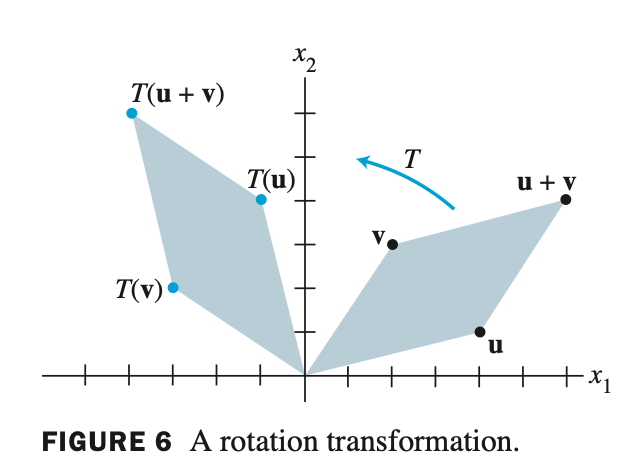
• linear transformation 을 통해 각도가 회전되었다.

• $T(\mathrm{u + v})$ 가 $T(\mathrm{u}) + T(\mathrm{v})$ 를 만족하는 linear 임을 확인할 수 있다.