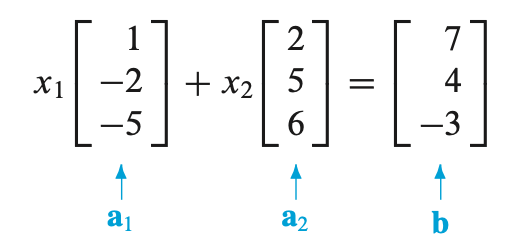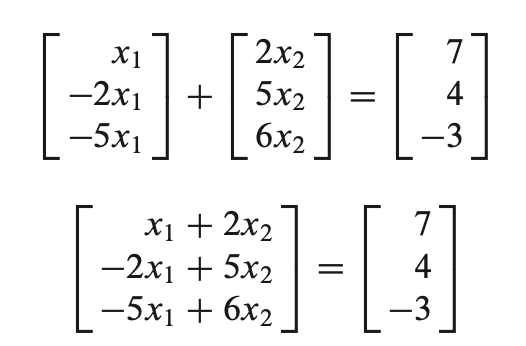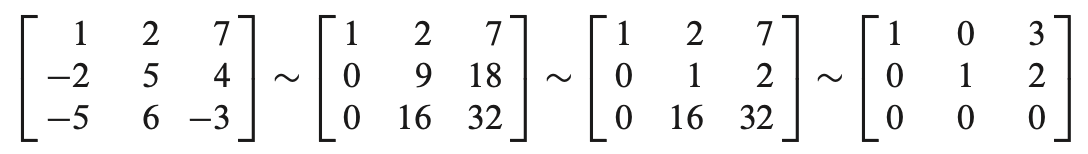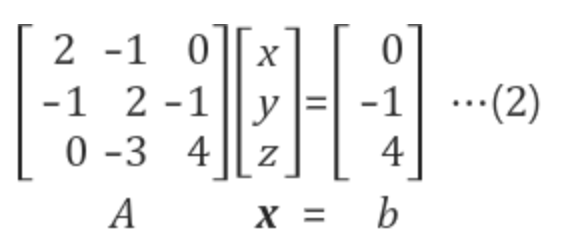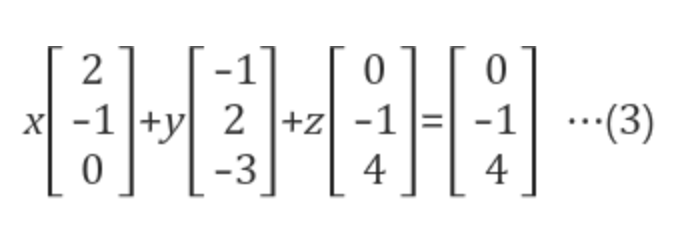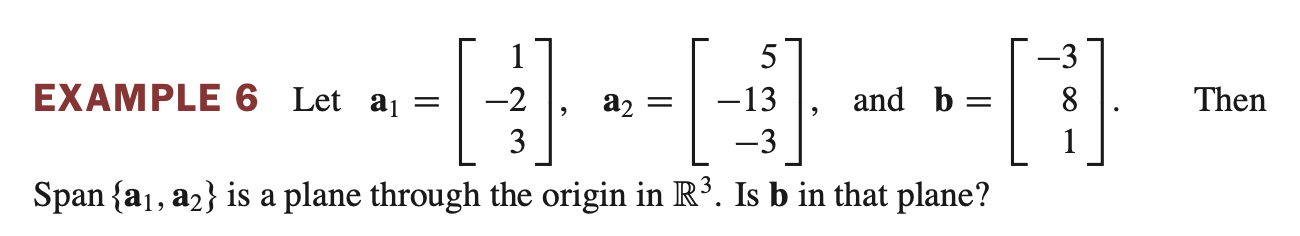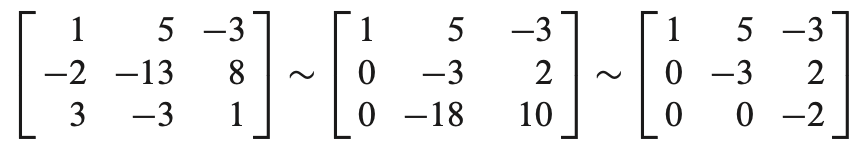용어 정리
- vectors in $ \mathbb{R}^{n} $ - algebraic properties (대수학적 성질)
- linear combination (선형 결합)
- vector equation (벡터 방정식)
- Span (공간을 포괄하다)
Vectors in $ \mathbb{R}^{2} $ - 2차원 실수체계에서의 벡터
$ \mathbb{R}^{2} $ 는 2차원 실수체계를 의미한다.
벡터의 표현 방법은 다음과 같다.
(1) 대괄호
\[\mathbf{u} = \begin{bmatrix} \phantom{-}3 \\\ -1 \quad \end{bmatrix} \quad \quad \mathbf{v} = \begin{bmatrix} .2 \\\ .3 \, \end{bmatrix} \quad \quad \mathbf{w} = \begin{bmatrix} w_1 \\\ w_2 \, \end{bmatrix}\](2) coordinate - 좌표
$ \mathbf{u} = (3, -1) \quad \mathbf{v} = (.2, .3) $
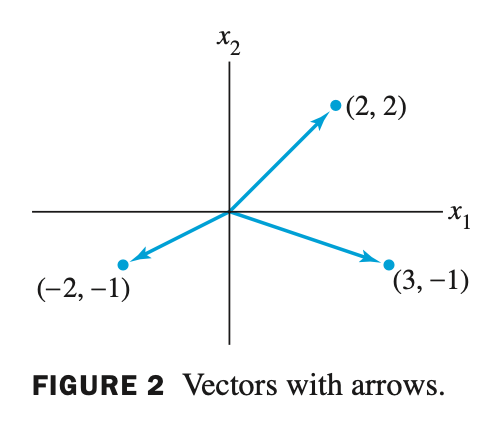
(3) arrows - 화살표
원점에서부터 vector point 까지 화살표를 그려 표현
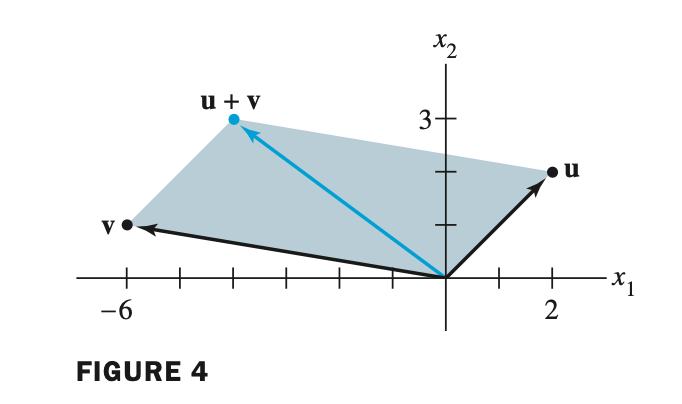
Vector summation - 벡터 덧셈
- 2차원 실수체계 공간에서 두 개의 벡터가 주어졌을때 덧셈이 가능
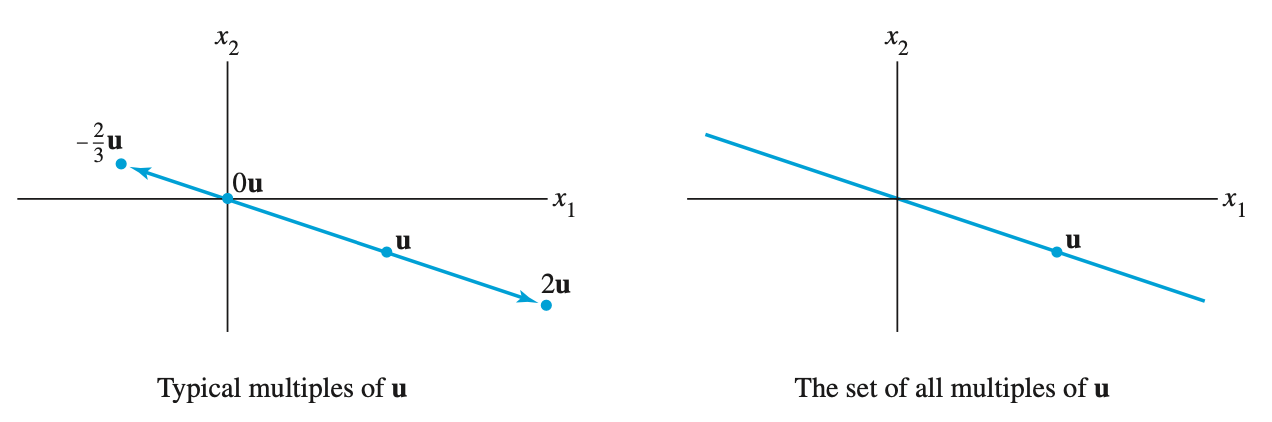
Scalar multiplication - 스칼라 곱
- 스칼라와 벡터를 곱할 수 있다. 스칼라는 단 하나의 값을 의미한다.
Geometric descriptions of $ \mathbb{R}^{2} $ - 2차원 실수체계 공간에서의 기하학적 표현
- 벡터를 다음과 같이 기하학적으로 표현이 가능하다.
(1) Geometric descriptions of vector summation
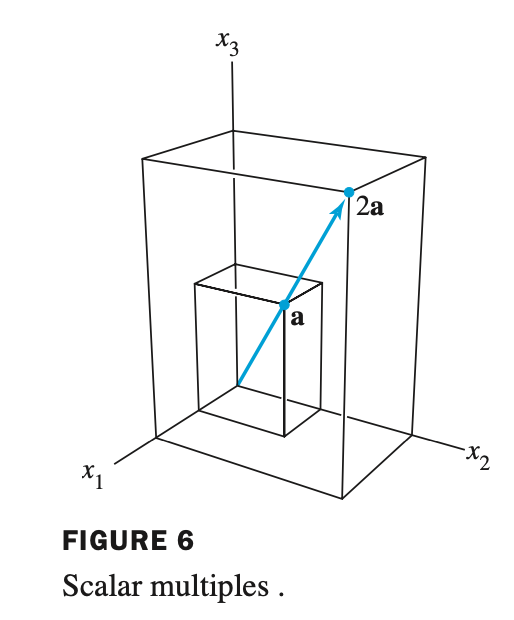
(2) Geometric descriptions of scalar multiplication
- 스칼라곱으로 u 벡터와 동일선상에 있는 모든 것을 표현할 수 있다.
Vectors in $ \mathbb{R}^{3} $ - 3차원 실수체계 공간에서의 벡터
$ \mathbf{a} = \begin{bmatrix} 1 \\ 5 \\ 4 \, \end{bmatrix}
\, $
Vectors in $ \mathbb{R}^{n} $ - n차원 실수체계 공간에서의 벡터
Algebraic properties of $ \mathbb{R}^{n} $ - $ \mathbb{R}^{n} $ 공간에서 대수학적 성질
- 이 8가지 성질은 당연한것같지만 만족하지 않는 세계도 존재한다.
- 벡터는 이 8가지 성질을 만족한다.
Linear combinations - 선형 결합
Given vectors $ v_1, v_2, \dots , v_p $ in $ \mathbb{R}^{n} $ and given scalars $ c_1, c_2, \dots , c_p $, the vector $ \mathbf{y} $ defined by \(\mathbf{y} = c_1\mathbf{v_1} + \dots + c_p\mathbf{v_p}\)
- 이것을 weights($ c_1, \dots, c_p $)가 있는 $ v_1, \dots, v_p $ 의 linear combination (선형 결합)이라고 한다.
- weights 는 각각의 vector에 곱해진 scalar를 의미한다.
벡터 방정식은 선형 시스템의 augmented matrix와 같은 해를 갖고 있다.
- vector equation과 augmented matrix는 same solution set을 갖고있다.
- $ a_1, a_2, b $ 가 주어졌을 때, $ a_1, a_2 $ 의 linear combination 으로 $ b $를 표현할 수 있다.
이제 이 augmented matrix에 row reduction을 이용해 reduced echelon form을 얻고 solution을 도출할 수 있다.
$ x_1 = 3, x_2 = 2 $ 의 solution 을 구할 수 있다.
Span {$ v_1, \dots, v_p $} 의 의미
- $ v_1, \dots, v_p $ 가 있을 때 span은 $ c_1v_1 + \dots + c_pv_p $ 형태의 linear combination을 의미한다.
- 즉, span은 linear combination을 간단히 표현한 것
Q1 Is a vector $ \mathbf{b} $ is span {$ v_1, \dots, v_p $}?
Q2 Does the following vector equation have a solution? $ x_1v_1 + x_2v_2 + \dots + x_nv_n = \mathbf{b} $
Q3 Does the following augmented matrix have a solution? $ \begin{bmatrix} v_1, \dots, v_n, \mathbf{b} \, \end{bmatrix} $Q1, Q2, Q3 세가지로 전부 다 나타낼 수 있다. Q1 $ \iff $ Q2 $ \iff $ Q3
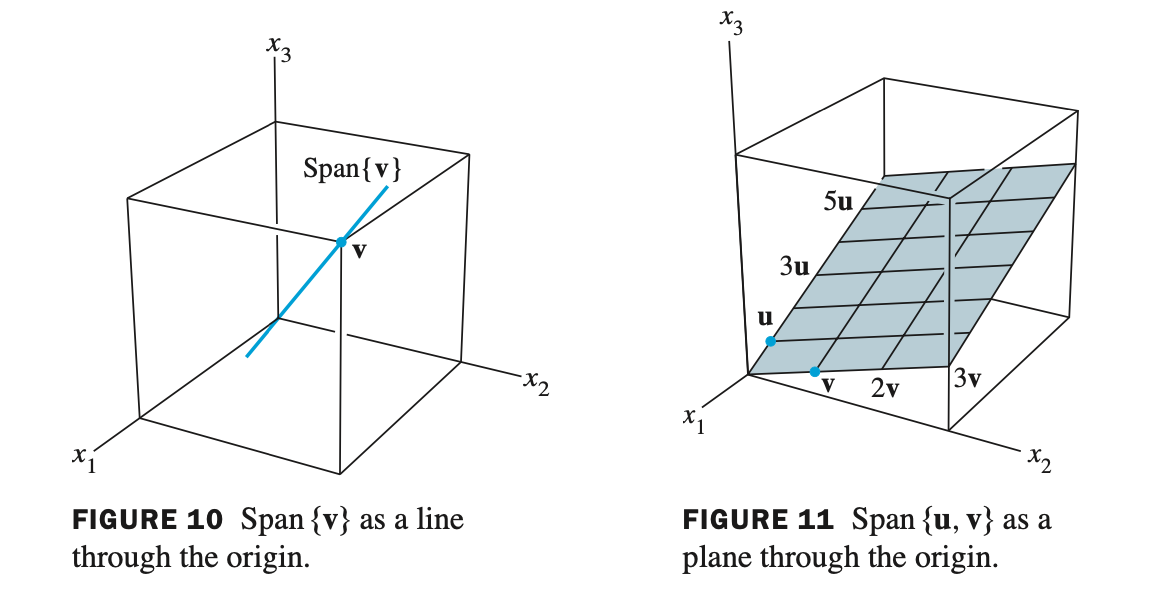
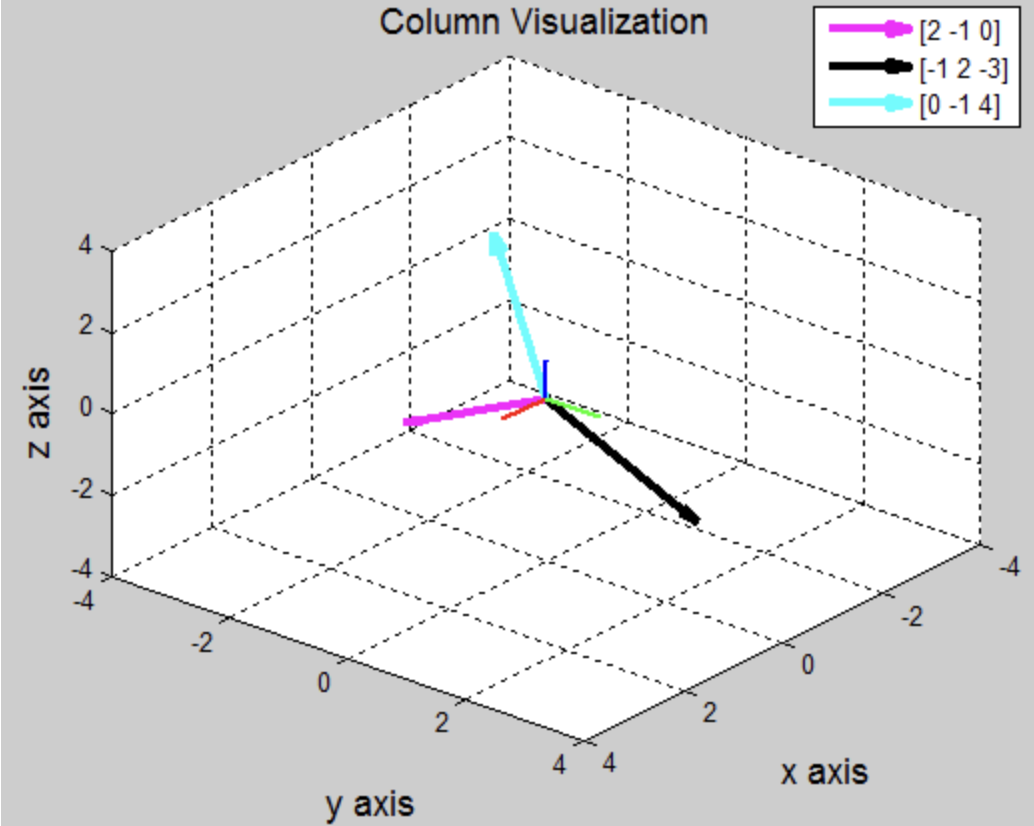
$ \mathbb{R}^{3} $ 공간에서 Span{v} 와 Span{u,v} 의 기하학적 표현
- Span{v} 는 3차원에서 직선
- Span{u,v} 는 3차원에서 평면으로 나타낼 수 있다.
- u와 v는 다른 벡터라는 조건에서 Span{u,v}로 표현이 가능하다.
- Row Picture와 Column Picture으로 분리해서 살펴보기
- 위 와 같은 3개의 방정식이 주어졌을때 Row Picture, Column Picture 두 가지 방법으로 행렬을 이해해보자.
우선 다음과 같이 Ax=b 형태의 Matrix Form을 만들어주자.
- Row Picture
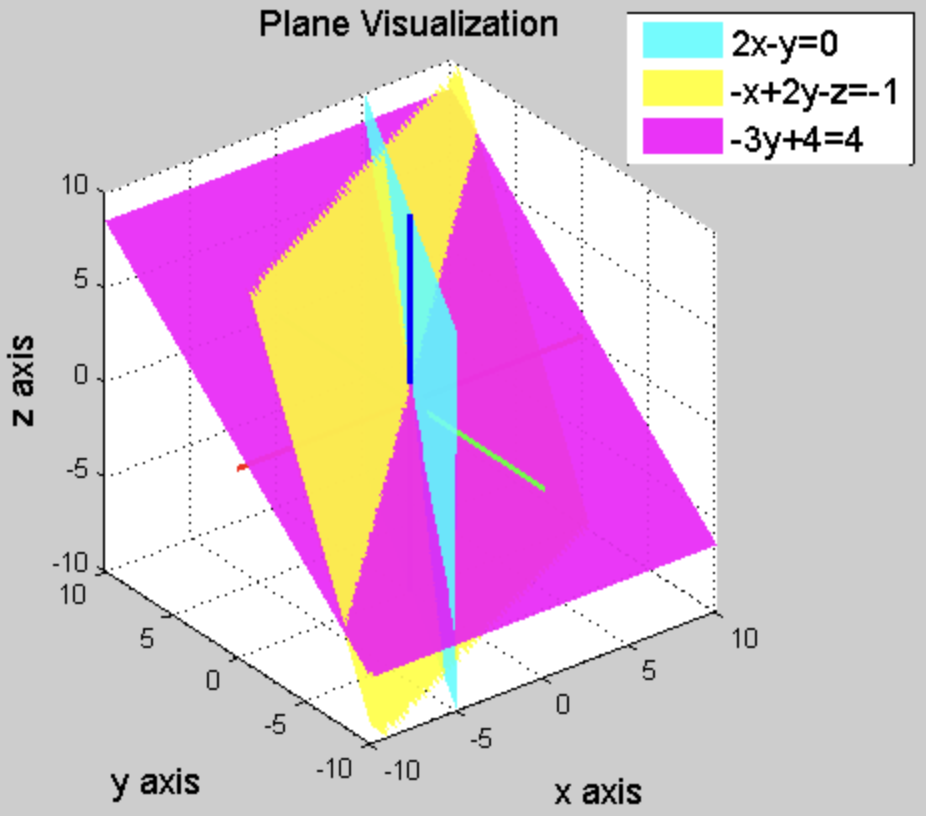
x,y,z 에 대해 평면 방정식을 공간상에 나타내보면 다음 그림과 같다.
- 3가지 평면은 딱 한 점에서 만나게 되고, 그것이 바로 이 시스템의 solution 이다.
- Column Picture
위 Matrix 를 3차원 벡터의 linear combination 형태로 나타내면 다음과 같다.
- 좌변이 나타내는 linear combination 이 어떤 우변의 벡터를 만들어내는것인지를 알아내야한다. x,y,z 에 어떤 값을 설정해야 우변이 만들어지는가와 같다.
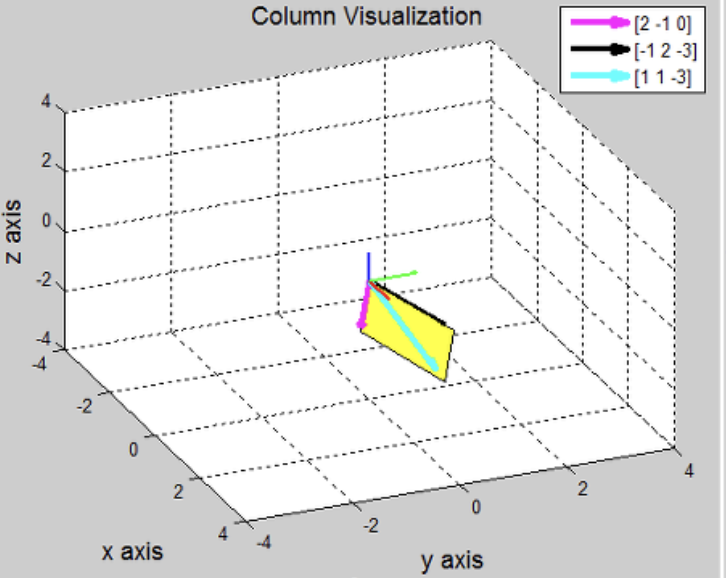
위 선형결합을 그림으로 나타내면 다음과 같다.
- 좌변의 선형결합으로 공간상의 모든 벡터(혹은 점)을 만들어낼 수 있는가를 생각해야한다.
여기서 더 나아가 살펴볼 점은 $v_3 = v_1 + v_2$ 를 의미하며 이것은 시스템 A에서 어떠 한 column 벡터가 나머지 두 벡터의 선형결합으로 이루어진 경우이고 이는 공간상에서 $v_3$ 는 $v_1, v_2$ 가 이루는 평면 위에 놓여져 있단 것이다.
- 이 경우 시스템 A는 어떤 선형조합을 해도 노란 평면을 벗어날 수 없다.
b가 Span{$ a_1, a_2 $}에 존재하는지 확인하기
$ a_1, a_2, b $를 augmented matrix로 표현하고 row reduction을 통해 reduced echelon form을 만들어 solution을 확인
- 여기서 3row를 방정식으로 표현하면, 0 = -2 가 되고 이는 inconsistent 즉 no solution 이므로
- b is not in Span{$ a_1, a_2 $}