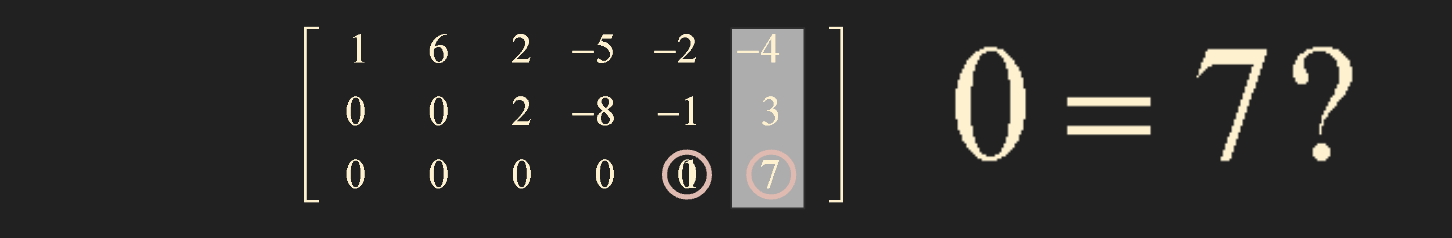용어 정리
- A nonzero row of column (0이 아닌 행과 열)
- A leading entry of row (행의 선행 성분)
- Echelon form (사다리꼴)
- Reduced echelon form (기약 사다리꼴)
- Uniqueness of the Reduced Echelon Form (기약 사다리꼴의 유일성)
- Row reduction algorithm (행령 표기법)
- Solution of linear systems (소거법)
- general solution (일반 해)
- basic variables (기본 변수)
- free variables (자유 변수)
- Existence and Uniqueness Theorem (유일성과 존재)
A nonzero row or column - 0 이 아닌 행렬
- 매트릭스에서 특정 row와 특정 column을 뽑아서 봤을 때 최소한 하나라도 0이 아니면 -> nonzero row, nonzero column 이라고 부른다.
A leading entry of row - 행의 선행성분
- the leftmost nonzero entry
- 0이 아닌 것 중에 제일 왼쪽에 있는 것이 leading entry에 해당됨
Echelon form - 사다리 꼴
- All nonzero rows are above any rows of all zeros.
모든 nonzero rows는 all zeros row 보다 위에 있다.
- Each leading entry of a row is in a column to the right of the leading entry of the row above it.
행의 leading entry는 위에 있는 leading entry보다 오른쪽 열에 있다.
- 빨간 점이 leading entry 이다.
- 1 row 의 leading entry 보다 2 row 의 leading entry 가 오른쪽에 있으니 Echelon Form 이 맞다.
Reduced echelon form - 기약 사다리 꼴
- 1강에서 했던 내용임
- The leading entry in each nonzero row is 1.
nonzero 행에 있는 leading entry는 1이다.
- Each leading entry is the only nonzero entry in its column.
leading entry 가 1이어야하고, leading entry column은 leading entry 를 제외하곤 전부 0이되어야한다.
- The leading entry in each nonzero row is 1.
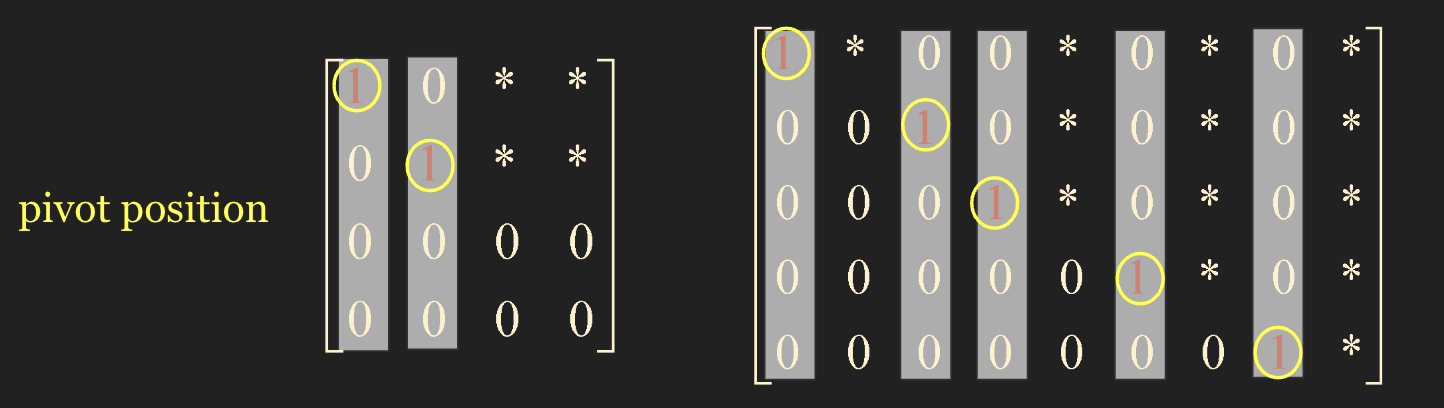
- pivot position : 1의 위치, reduced echelon form이아니고 그냥 echelon form 만되어도 reduced echelon form 이된다.
Theorem1. Uniqueness of the Reduced Echelon Form
Each matrix is row equivalent to one and only one reduced echelon matrix.
- Theorem1. Uniqueness of the Reduced Echelon Form
- Each matrix is row equivalent to one and only one reduced echelon matrix.
- 각 매트릭스는 Reduced Echelon Form 이 딱 하나 밖에 없다. row reduction을 통해 row equivalent 를 얻을 수 있음
Row reduction algorithm - 행 줄임 알고리즘
Step1. begin with the leftmost nonzero column
Step2. select a nonzero entry in the pivot column as a pivot. If necessary, interchange rows to move this entry into the pivot position
- pivot position 이 0이 되면 안되므로 interchange를 통해 row 를 바꿔주자.
Step3 row replacement to create zeros in all positions below the pivot
- pivot position을 제외한 pivot column에 있는 나머지들을 전부 0으로 만들어주기
Step4 apply steps 1-3 to the submatrix that remain
남은것에 대해 step 1-3 반복 수행
~ 표시는 row equivalent 하다는 뜻, 즉 row reduction을 통해서 얻을 수 있다.
- The combination of steps 1-4 is called forwad phase
- 이 결과물이 -> echelon form! 이다
- 이 echelon form을 redouced echelon form 으로 만드는 것은
Step5 Beginning with the rightmost pivot and working upward and to the left, create zeros above each pivot.
If a pivot is not 1, make it 1 by a scaling operation.
맨 오른쪽에 있는 pivot 부터 이번에는 위에 있는 것들을 전부 0으로 만들어준다.
- Step 5 is called backward phase
- 이렇게 backward phase 까지 진행했으면 reduced echelon form 이 나온거고 이를 통해 솔루션을 얻을 수 있다.
Solution of linear systems - 선형 시스템의 해
- augmented matrix 를 row reduction 알고리즘으로 reduced echelon form을 만들면 선형방정식의 해를 쉽게 구할 수 있다.
- row reduction 으로 구한 reduced echelon form 형태의 augmented matrix
- 이를 lineqr equation 으로 표현해보자.
- 위 lineqr equation의 해를 구하면 다음과 같다.
- 여기서 중요한 것은 general solution (일반 해), basic variable (기본 변수), free varialbe (자유 변수) 가 무엇인지 확실하게 짚고 넘어가야 한다.
(1) free variable - 자유 변수
\[x_3 \; is \; free\]- $ x_3 $ 을 free variable 이라고 한다.
- $ x_3 $ 을 어떤 값으로 두어도 0 = 0 을 만족한다.
(2) basic variable - 기본 변수
- basic variable 은 free variable 로 표현한 것을 의미
(3) general solution - 일반 해
\[\begin{cases} x_1 = 1 + 5x_3 \\ x_2 = 4 - x_3 \\ x_3 \; is \; free \end{cases}\]general solution 은 basic variable 과 free variable 로 표현된 해를 의미한다.
- 해가 무한대로 존재한다. 이럴 때는 $x_3$라는 것을 free variable 으로 둔다.
- $x_1, x_2, x_3$ 이 중 어떤것이든 free variable 로 하지 않고 $x_1, x_2$ 같이 leading variables 에 포함되는 변수들을 basic varialbes로 잡고
- $x_3$를 free variable 로 정하기로 약속.
- 이런식으로 표현된 솔루션을 -> general solution
find the general solution of the following augumented matrix - augmented matrix 에서 general solution 찾기
- augmented matrix 를 row reduce
- backward phase 를 통해 0으로 만들고 row reduction 진행
- 여기서 leading variable에 해당되는것은 $x_1, x_3, x_5$ 이고 free variable은 $x_2, x_4$이다.
- reduced echelon form 을 linear equation 으로 표현한다.
- general solution 을 다음과 같이 표현할 수 있다.
하지만 여기서 모순점이 발생한다. $ 0 = 7 $ 은 모순이므로 이 linear system 은 inconsistent 하므로 no solution 이다.
Theorem2. Existence and Uniqueness Theorem
A linear system is consistent if and only if the rightmost column of the augumented matrix is not a pivot column - that is, if and only if an echelon form of the augumented matrix has no row of the forms.
\(\begin{bmatrix} 0 & \cdots & 0 & b \end{bmatrix} \quad\) with $ \; b \; $ is nonzero
If a linear system is consistent, then the solution set contains either (i) a unique solution, when there are no free variables, of (ii) infinitely many solutions, whene there is at least one free variables.
- 이를 정리하자면 다음과 같다.
- lineqr equation 이 consistent 하면 augmented matrix에서 b가 pivot position이 아니다.
- 즉, b를 제외하고 0인 행렬이 있으면 안된다.
반대로, 0 & \cdots & 0 & b 인 row 가 있으면 -> no solution 이다.
- linear system 이 consistent 하면, (i) free variable 이 없다면 exactly one solution (trivial solution) 이다.
- (ii) 1개 이상의 free variable 이 있다면 infinitely many solution (nontrivial solution) 이다.
- 즉, 해가 1개 -> free variable 이 존재하지 않고 해가 무수히 많다면 -> at least one free variable 이 존재한다.
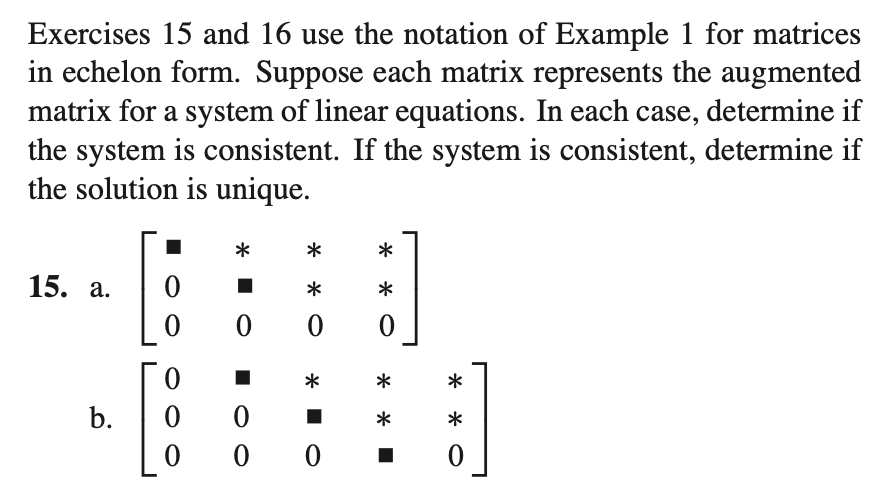
예제 더 풀어보기
- a. 는 $ x_3 $ 가 free variable 이므로 consistent, many solutions 이다.
- b. 는 첫번째 column 이 전부 0 이므로 $ x_1 $ 이 free variable 이 되므로 consistent, many solutions 이다.