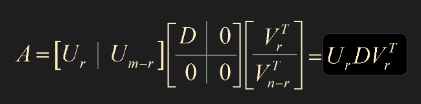Hits

용어 정리

  • Pseudoinverse - 유사역행렬
  • Hermitian matrix - 에르미트 행렬
  • tridiagonal - 삼중 대각 행렬 (upper band = 1, lower band = 1)
  • Toeplitz matrix - 테플리츠 행렬
  • Circulant matrix - 순환 행렬
  • Iterative Method - 반복법


Reduced SVD

  • 6.4 에서 $\mathbf{u}_1 , \dots $ 벡터들을 확장하는 과정이 매우 복잡하고 계산이 힘들었었다. 하지만 Reduced SVD 를 사용하면 확장하는 과정이 필요가 없어진다.
  • 보통 대부분 SVD 를 한다고 하면 훨씬 더 효율적인 Reduced SVD 를 사용한다.


\[A = U \Sigma V^T\]
  • 위 SVD 공식에서 $\Sigma$ 는 singular values 를 diagonal terms 으로 두는 diagonal matrix $D$ 와 0의 block matrix 이다. $\Sigma = \begin{bmatrix} D & 0 \\ 0 & 0 \end{bmatrix}$
  • 마찬가지로 $U, V$ 행렬도 block matrix 형태로 나타내보자.
\[U = \begin{bmatrix} \mathbf{u}_1 & \dots & \mathbf{u}_m \end{bmatrix} = \begin{bmatrix} U_r & U_{m - r} \end{bmatrix}\]
  • 여기서 $U_r = \begin{bmatrix} \mathbf{u}_1 & \dots & \mathbf{u}_r \end{bmatrix} $ 이다. 우리가 쉽게 구했었던 것들임. 다만 여기서 $\mathbf{u}_r$ 이상부터 확장하는 과정이 복잡했을 뿐이다.
  • 마찬가지로 $V$ 역시 다음과 같이 표현이 가능하다.
\[V = \begin{bmatrix} \mathbf{v}_1 & \mathbf{v}_2 & \dots & \mathbf{v}_n \end{bmatrix} = \begin{bmatrix} V_r & V_{n -r} \end{bmatrix}\]
  • 여기서 $V_r = \begin{bmatrix} \mathbf{v}_1 & \dots & \mathbf{v}_r \end{bmatrix} $


\[A = \begin{bmatrix} U_r & U_{m - r} \end{bmatrix} \begin{bmatrix} D & 0 \\\ 0 & 0 \end{bmatrix} \begin{bmatrix} V_r^T \\\ V_{n-r}^T \end{bmatrix} = U_r D V_r^T\]



Desktop View

  • 정리해보면, 이전에는 \(\mathbf{u}_{r+1} , \dots , \mathbf{u}_m\) 까지 확장해서 구해야 했던 것들을 Reduced SVD 를 사용하여 $\mathbf{u}_1, \dots, \mathbf{u}_r$ 까지만 알면 풀 수 있다는 것이다. $\mathbf{v}$ 도 마찬가지!



Pesudoinverse (the Moore-Penrose Inverse) - 유사역행렬

  • 유사역행렬은 $A^+$ 를 정의해서 least-square solution 을 구하는데 이용한다.
\[A = U_r D V_r^T\]
  • 위와 같이 Reduced SVD 에서 $A$ 행렬의 역행렬이 존재하는지, square matrix 인지도 모르는 상황이다.
  • 다만, $D$ 행렬은 $r \times r$ matrix 이고 nonzero diagonal terms 를 가지기 때문에 역행렬이 존재한다.
  • 따라서 다음과 같이 정의할 수 있다.
\[A^+ = V_rD^{-1}U_r^T\]
  • 우리가 $A\mathbf{x} = \mathbf{b}$ 의 linear equation 을 풀고자 할 때, $\widehat{\mathbf{x}}$ 을 다음과 같이 정의한다.
  • $A^+$ 에 위에서 정의한 내용을 대입해보면
\[\widehat{\mathbf{x}} = A^+ \mathbf{b} = V_r D^{-1} U_r^T \mathbf{b}\]
  • 여기서 양변에 $A$ 행렬을 multiplication 해주면
\[A\widehat{\mathbf{x}} = AV_r D^{-1} U_r^T \mathbf{b} = U_r D V_r^T V_r D^{-1} U_r^T \mathbf{b}\]
  • 여기서 $V$ 행렬이 square matrix 라는 보장이 없고 orthonormal columns 를 갖고 있으므로(5.2 단원 theorem 6)
  • $V_r^T V_r = I , DD^{-1} = I$ 가 되므로
\[= U_rU_r^T \mathbf{b}\]
\[\mbox{proj}_w \mathbf{y} = UU^T\mathbf{y}\]
  • 따라서 $\mathbf{b}$ 를 Col $A$ 에 projection 한 것과 동일하다.
\[U_rU_r^T \mathbf{b} = \widehat{\mathbf{b}}\]

  • 결국에는 $A\widehat{\mathbf{x}}$ 는 $\mathbf{b}$ 를 Col $A$ 에 projection 한 것이고, $\widehat{\mathbf{x}}$ 은 $A\mathbf{x} = \mathbf{b}$ 의 least-squares solution 이 된다.

  • 또한 $\widehat{\mathbf{x}}$ 은 $A\mathbf{x} = \mathbf{b}$ 의 least-squares solution 중에서도 가장 작은 값이다.



Applications

  • SVD 를 어디에 이용할 수 있냐면, $A\mathbf{x} = \mathbf{b}$ 의 least-squares solution (length 가 제일 작은) 을 구할 때 쓸 수 있다. 즉 모든 linear equation 에서 사용이 가능하다.
  • data analysis(covariance matrix) 에서 사용
  • 이미지, 사운드 프로세싱에서 사용, 특히 singular value 의 값이 0에 매우 근접할 경우 그 일부를 잘라내어 근사하는 방법을 사용하기도 한다. (Truncated SVD)



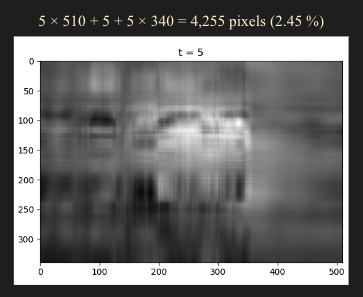
Example of Image Processing

  • 원본 이미지
  • $510 \times 340 = 173,400$ 개의 픽셀들이 저장된 원본 이미지의 singular values 를 잘라내는 Truncated SVD 를 사용해보면 Desktop View


  • $t = 5$ 5개의 singular values 만 남겨놓았을 때, 이미지를 구분하기 힘들다. Desktop View


  • 하지만 $t = 50$ 정도만 되어도 원본 이미지와 육안으로 차이점을 찾기 어렵다.
  • 여기서 173,400 픽셀 -> 42,550 픽셀로 원본 이미지 기준 24.5% 까지 압축이 가능하다.
  • 마찬가지로 $t = 100$ 일 경우는 49.1% 까지 압축이 가능하다.

Desktop View

  • 따라서 우린 SVD 를 통해서 노이즈를 제거하거나 이미지 압축률을 개선할 수 있다.



Matrix Classification

  • 우리가 배운 내용을 토대로 어떤 행렬이 주어졌을 때, 행렬의 성질로 구분해보자.


  • 실수 체계
  • real matrix 일 때는 크게 symmetric matrix 인지 non-symmetric matrix 인지 구분할 수 있다.
  • 특히, symmetric matrix 에서는 다음과 같이 분류할 수 있는데
  • Positive definite
  • Negative definite
  • Indefinite
  • 보통 수치 해석 알고리즘에서 제일 선호하는 것은 positive definite 이다.


  • 허수 체계
  • complex matrix 일 때는 크게 hermitian matrix 인지 non-hermitian matrix 인지 구분할 수 있다.
  • 여기서 hermitian matrix 는 symmetric matrix 를 확장한 개념이라고 생각하면 된다. symmetric matrix 의 성질들이 보통 hermitian matrix 에도 적용이 되기 때문에 확장된 개념이다.
\[A = A^* \quad \mbox{equals} \quad A = \overline{A^T}\]
  • 행렬 $A$ 와 $A$ 에 conjugate transpose 를 취한 $A^*$ 가 동일할 때 hermitian matrix 라고 한다.
  • hermitian matrix 도 다음과 같이 분류할 수 있다.
  • Positive definite ( \(\mathbf{x}^* A \mathbf{x} > 0\) )
  • Negative definite
  • Indefinite
  • complex, hermitian 형태는 실생활에서 양자역학, 동역학에서 많이 나온다. 또한 어떤 자연 현상, 물리 현상, 공간을 차분화해서 수식을 쓰면 보통 positive definite 일 가능성이 높다.
  • positive definite 일 경우 관련 알고리즘들이 잘 적립되어 있어 문제를 풀기가 상대적으로 쉽다. 따라서 positive definite 일 경우 매우 운이 좋은 케이스라고들 한다.


  • Positive definite 일 경우 행렬을 푸는 방법

Cholesky decomposition
real matrix : \(A = R^TR = LL^T\)
complex matrix : \(A = R^*R = LL^*\)

LDL decomposition
real matrix : \(A = UDU^T = LDL^T\)
complex matrix : \(A = UDU^* = LDL^*\)

  • 주의, 여기서 upper triangular matrix $U$ 와 lower triangular matrix $L$ 의 diagonal term 은 1이 되는 형태가 된다.
  • 또한, LDL decomposition 의 경우 tridiagonal 행렬 형태로 나왔을 때 적용해서 푼다.


  • Indefinite 일 경우 행렬을 푸는 방법

Diagonal Pivoting Method
real matrix : \(UDU^T = LDL^T\)
complex matrix : \(UDU^* = LDL^*\)

  • 주의, 여기서 $D$ 는 diagonal matrix 가 아니라, block diagonal matrix 이다. block 형태는 최대 $2 \times 2$ 까지이다. ($1 \times 1$ , $2 \times 2$)
  • 위 decomposition 으로 $A\mathbf{x} = \mathbf{b}$ 형태의 방정식을 풀 수 있다.


  • 상대적으로 위 알고리즘에 비해 비효율적인 LU Decomposition 이나, $n^3$ 의 시간복잡도를 가진 Gauss elimination 을 사용하지 않고 위 방법들을 주로 사용한다.
  • 컴퓨팅적 측면에서 계산 속도, 정확도, 안정성 등을 평가해서 최적의 알고리즘을 사용해야한다.



Complex Symmetric Matrix

  • complex symmetric matrix 는 얼핏보면 hermitian matrix 인가 싶을수도 있는데 완전히 구분된 다른 형태의 행렬이다. complex symmetric matrix 는 hermitian matrix 가 아니다.
  • complex symmetric matrix 인 $A$ 행렬이 있을 때 conjugate transpose 를 취한 행렬과 같은게 아니다. 반드시 symmetric matrix 처럼 그냥 transpose 를 취했을때 같은 행렬이 된다.

  • 주로 boundary integral equations 분야에서 주로 많이 나온다.

  • complex symmetric matrix 는 Diagonal pivoting method 를 사용해서 푼다. real symmetric matrix 를 풀듯이 풀면 된다. (주의 $A = UDU^* = LDL^*$ 로 푸는게 아니다.)
\[A = UDU^T = LDL^T\]



Matrix 를 모양으로 classification

  • Full matrix
  • 일반적인 행렬의 형태

Desktop View

  • Band matrix
  • diagonal term 인 밴드를 기준으로 위쪽 파랑색은 upper bandwidth, 아래쪽 검정색은 lower bandwidth 라고 표현한다.

Desktop View


  • 행렬이 band matrix 형태로 나오면 저장 용량을 아끼기 위해서 Full matrix 형태로 저장하지 않고 row, column 형태로 변환하여 저장을 한다.
  • 퍼포먼스 때문에 보통 2D 형태로 저장하지 않고, 1 Dimensional Vector 형태로 저장한다.


  • 위에서 언급한 tridiagonal 형태는 이 band matrix 의 upper bandwidth = lower bandwidth = 1 인 경우이다.
  • tridiagonal matrix 는 1D FDM(Finite Difference Method) 방법론에서 주로 나온다.



특별한 Matrix

  • Toeplitz matrix
  • $m \times m$ matrix 이고, 각 band 의 diagonal term 즉 대각선항들이 다 똑같은 경우이다.

Desktop View

  • 이 행렬은 주로 Levinson-Durbin recursion 을 사용하여 푸는데, $\sim n^2$ 정도 소요된다. 특히 이 방법은 필요한 저장공간이 단 하나의 column 만을 요구하기에 \(a_0, a_1, a_2, \dots, a_{n-1}\) 공간복잡도는 $n$ 이다!!

  • 하지만 Levinson-Durbin recursion 은 stability 즉 안정성 쪽에서 이슈가 존재하여 문제가 제대로 안풀리거나 정확도가 떨어질 수 있다.

  • 따라서, Bareiss algorithm 을 사용하기도 한다. 마찬가지로 속도는 $\sim n^2$ 정도 소요되는데, 다만 이 방법은 필요한 저장공간이 Full matrix 를 통째로 저장해야하기 떄문에(공간복잡도 $n^2$) Levinson-Durbin recursion 으로 먼저 문제를 풀고 이슈가 발생하면 Bareiss algorithm을 사용한다.



  • Circulant matrix
  • Toeplitz matrix 처럼 마찬가지로 대각선항들이 다 같지만, column 형태로 보면 한칸씩 밀려서 순환되는 패턴을 발견할 수 있다.

Desktop View

  • 이 행렬의 경우 matrix equation 을 푸는 방법이 아니라 circular convolution theorem 을 적용해서 Discrete Fourier Transform 을 사용하여 문제를 푼다. 여기서 Fast Fourier Transform 을 사용하여 $\sim n \log (n)$ 의 속도로 매우 효율적인 편이다.


  • 위 행렬들은 주로 digital image processing, signal processing, cryptography 등 다양한 분야에서 쓰인다.



Iterative Method

  • 보통 공학문제들은 공간에 대해 차분화를 하고 continuous equation 을 discrete equation 으로 변환하면 matrix equation 이 나오게 된다.
  • 하지만 $A\mathbf{x} = \mathbf{b}$ 형태를 차분화하면 굉장히 거대한 크기의 행렬이 되거나 많은 부분이 0이 되는데, 앞에서 거론한 방법들을 적용하면 속도도 느리고, 저장공간 측면에서 매우 불리해진다. (보통 기가바이트, 테라바이트 단위의 용량이 필요한 행렬)
  • 따라서 위와 같은 경우 Iterative Method (반복법) 를 사용한다.


  • 주로 Jacobi Method, Gauss-Seidel, Successive over-relaxation (SOR) 이 세 가지가 가장 기본적이다.
  • 추가적으로, Conjugate Gradeint(CG) , BiCG, BiCG-Stab, generalized minimal residual method (GMRES) 등의 반복법들이 있다.