---

용어 정리

• Quadratic Forms - 이차 형식
• degree - 차수
• The matrix of the quadratic form - 이차 형식의 행렬
• The Principal Axes Theorem - 주축 정리
• Classifying Quadratic Form - 이차 형식 분류하기

Quadratic Form - 이차 형식

• $\mathbf{x}$ 가 $\mathbb{R}^n$ space 에 존재하고 $\mathbf{x}$ 는 $(x_1, x_2)$ 라고 가정하자

\[\mathbf{x}^T \mathbf{x} = x_1^2 + x_2^2 + \dots + x_n^2\]

• 이처럼 각각의 entry 들의 차수가 모두 2인 형태임을 확인할 수 있다. 다른 예시를 살펴보자.

\[4x_1^2 + 2x_2^2 - 5x_3^2\]

• 위 식을 다음과 같이 matrix multiplication 형태로 표현할 수 있다.

\[\mathbf{x}^T \begin{bmatrix} 4 & 0 & 0 \\\ 0 & 2 & 0 \\\ 0 & 0 & -5 \end{bmatrix} \mathbf{x} = \begin{bmatrix} x_1 & x_2 & x_3 \end{bmatrix} \begin{bmatrix} 4x_1 \\\ 2x_2 \\\ -5x_3 \end{bmatrix} = 4x_1^2 + 2x_2^2 - 5x_3^2\]

• matrix multiplication 을 전개하여 계산해보면 원래의 식과 동일함을 확인할 수 있다. 다음 식 역시 모든 entry 들이 2차인 quadratic form 이다.

\[x_1^2 + 4x_2^2 -2x_1x_2 = \mathbf{x}^T \begin{bmatrix} 1 & -1 \\\ -1 & 4 \end{bmatrix} \mathbf{x}\]

• $x_1x_2$ 의 차수 역시 2차수이다. 이런 형태를 cross-product 라고 부른다.

• 위 내용을 정리해보면, Quadratic Form 이란 모든 term 들이 2차수인 다항식(a polynomial with terms all of degree two)을 의미하며 다음과 같이 나타낼 수 있다.

\[Q(\mathbf{x}) = \mathbf{x}^T A \mathbf{x}\]

• 여기서 $A$ 행렬은 $n \times n$ 크기의 symmetric matrix 이고 the matrix of the quadratic form (= quadratic matrix) 라고 불린다.

Example 1

Let $\mathbf{x} = (x_1, x_2)$ , Compute $\mathbf{x}^TA\mathbf{x}$ for the following matrices :

\[\mbox{a. } \; A = \begin{bmatrix} 4 & 0 \\\ 0 & 3 \end{bmatrix} \quad \quad \mbox{b. } \; A = \begin{bmatrix} 3 & -2 \\\ -2 & 7 \end{bmatrix}\]

• a. 풀이

\[\begin{bmatrix} x_1 & x_2 \end{bmatrix} \begin{bmatrix} 4 & 0 \\\ 0 & 3 \end{bmatrix} \begin{bmatrix} x_1 \\\ x_2 \end{bmatrix} = \begin{bmatrix} x_1 & x_2 \end{bmatrix} \begin{bmatrix} 4x_1 \\\ 3x_2 \end{bmatrix} = 4x_1^2 + 3x_2^2\]

• $A$ 의 diagonal term 들이 $x_1, x_2$ 의 weight 가 되었다.

• b. 풀이

\[\begin{bmatrix} x_1 & x_2 \end{bmatrix} \begin{bmatrix} 3 & -2 \\\ -2 & 7 \end{bmatrix} \begin{bmatrix} x_1 \\\ x_2 \end{bmatrix} = \begin{bmatrix} x_1 & x_2 \end{bmatrix} \begin{bmatrix} 3x_1 -2x_2 \\\ -2x_1 + 7x_2 \end{bmatrix}\] \[= x_1(3x_1 - 2x_2) + x_2(-2x_1 + 7x_2) = 3x_1^2 -2x_1x_2 -2x_1x_2 + 7x_2^2\] \[= 3x_1^2 - 4x_1x_2 + 7x_2^2\]

• $A$ 행렬에 -2 라는 요소가 생겼음을 확인할 수 있다. 그리고 -2 요소로 인해 cross-product term 인 $-4x_1x_2$ 가 생겼다. cross-product term 이 존재하면 기하학적 표현이나 계산이 매우 복잡해진다.

Example 2

For $\mathbf{x}$ in $\mathbb{R}^n$ , let $Q(\mathbf{x}) = 5x_1^2 + 3x_2^2 + 2x_3^2 - x_1x_2 + 8x_2x_3 $ . Write this quadratic form as $\mathbf{x}^T A \mathbf{x}$

• quadratic form 의 cross-product term 을 $A$ 행렬로 표현할 때 $-x_1x_2$ 의 경우 $a_{12}, a_{21}$ 에 -1을 2로 나눈 값들을 넣어주면 되고, $8x_2x_3$ 의 경우 $a_{23}, a{32}$ 에 8을 2로 나눈 값들을 넣어주면된다.

• cross-product term 을 제외한 나머지($5x_1^2 + 3x_2^2 + 2x_3^2$)는 그대로 5,3,2 가 diagonal term 으로 들어가게 된다. 그 외는 0을 넣어준다.

\[Q(\mathbf{x}) = \mathbf{x}^T A \mathbf{x} = \begin{bmatrix} x_1 & x_2 & x_3 \end{bmatrix} \begin{bmatrix} 5 & -1/2 & 0 \\\ -1/2 & 3 & 4 \\\ 0 & 4 & 2 \end{bmatrix} \begin{bmatrix} x_1 \\\ x_2 \\\ x_3 \end{bmatrix}\]

• 다시 matrix multiplication 을 전개하면 같은 식이 나옴을 확인할 수 있다. 또한 $A$ 행렬을 transpose 해보면 symmetric 한 성질임을 확인할 수 있다.

Change of Variable in a Quadratic Form - 이차 형식에서 변수 변경

• quadratic form 에서 변수를 변경하여 cross-product term 을 제거할 수 있다. cross-product term 을 제거하면 quadratic form 을 좀 더 쉽게 사용할 수 있다.

• $\mathbf{x}$ 를 다음과 같이 표현할 수 있다.

\[\mathbf{x} = P \mathbf{y}\] \[\mathbf{y} = P^{-1}\mathbf{x}\]

• 여기서 $P = [\mathbf{b}_1 \quad \mathbf{b}_2 \quad \dots \quad \mathbf{b}_n]$ 이라고 가정하면 다음과 같이 표현할 수 있다.

\[\mathbf{x} = y_1 \mathbf{b}_1 + y_2 \mathbf{b}_2 + \dots + y_n \mathbf{b}_n\]

• 여기서 $\mathbf{y}$ 는 $\mathbf{x}$ 의 coordinate vector 로 표현할 수 있다.
• 즉 $P$ 는 $A$ 행렬의 eigenvector 이다. $A$ 행렬이 symmetric 이면, $P$ 의 column 들은 직교한다. 그말은 $A$ 행렬은 orthogonally diagonalizable 하다는 뜻이므로
• quadratic form 에 $\mathbf{x} = P\mathbf{y}$ 를 대입해보자.

\[\mathbf{x}^T A \mathbf{x} = (P\mathbf{y})^T A (P\mathbf{y}) = \mathbf{y}^TP^TAP\mathbf{y} = \mathbf{y}^T(P^TAP)\mathbf{y}\]

• $P^TAP$ 는 대각화 정리에 의해 $D$ 가 된다. 따라서 최종적으로 다음과 같이 변경된다.

\[\mathbf{y}^TD\mathbf{y}\]

• $D$ 의 diagonal term 들은 $A$ 행렬의 eigenvalue 이다.
• quadratic form 이 $ \mathbf{y}^TD\mathbf{y} $ 로 변경되어 cross-product term 들이 제거된다.

Example 3

Make a change of variable that transforms the quadratic form
\(Q(\mathbf{x}) = \mathbf{x}^T \begin{bmatrix} 1 & -4 \\\ -4 & -5 \end{bmatrix} \mathbf{x}\) into a quadratic form with no cross-product term.

• cross-product term 이 존재하기 때문에 $\mathbf{y}^TD\mathbf{y}$ 으로 change of variable 을 취해준다. 그러기 위해서는 $A$ 행렬을 orthogonally diagonalize 를 해줘야한다.
• characteristic equation 을 통해 $A$ 행렬의 eigenvalue 와 eigenvector 를 찾으면 다음과 같다.

\[\lambda = 3 : \begin{bmatrix} 2/\sqrt{5} \\\ -1/\sqrt{5} \end{bmatrix} \; , \quad \lambda = -7 : \begin{bmatrix} 1/\sqrt{5} \\\ 2/\sqrt{5} \end{bmatrix}\]

• $P$ 와 $D$ 행렬을 만들면

\[P = \begin{bmatrix} 2/\sqrt{5} & 1/\sqrt{5} \\\ -1/\sqrt{5} & 2/\sqrt{5} \end{bmatrix} \; , \quad D = \begin{bmatrix} 3 & 0 \\\ 0 & -7 \end{bmatrix}\]

• 다음 식을 $A = PDP^{-1}$ $D$ 에 대해 풀어보면

\[D = P^{-1}AP = P^TAP\]

• 이제 $\mathbf{x} = P\mathbf{y}$ 로 변경하고 quadratic form 에 대입해준다.

\[x_1^2 - 8x_1x_2 - 5x_2^2 = \mathbf{x}^TA\mathbf{x} = (P\mathbf{y})^TA(P\mathbf{y}) = \mathbf{y}^TP^TAP\mathbf{y} = \mathbf{y}^TD\mathbf{y}\] \[= 3y_1^2 - 7y_2^2\]

• 이렇게 cross-product term 이 제거가 된것을 확인할 수 있다.
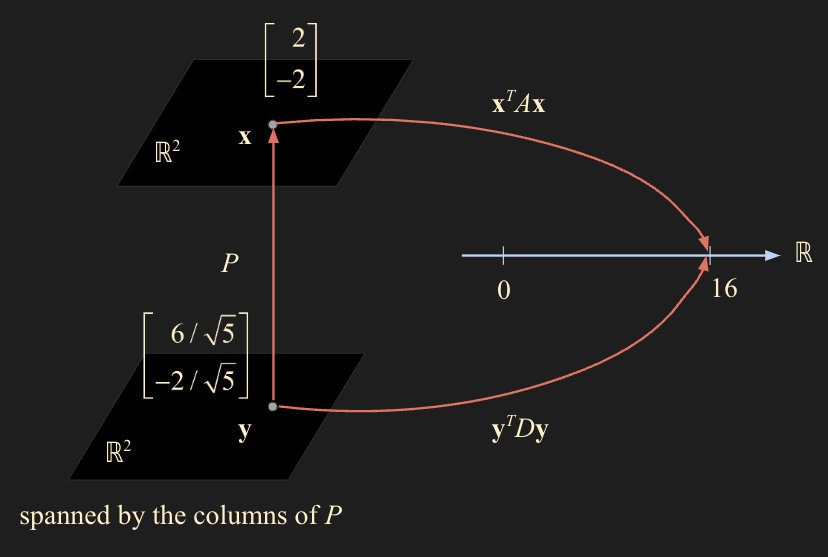
• 또한 우리는 다음과 같은 성질을 발견할 수 있다. 만약 $\mathbf{x} = (2, -2)$ 라고 가정해보면

\[Q(\mathbf{x}) = \mathbf{x}^TA\mathbf{x} = \begin{bmatrix} 2 & -2 \end{bmatrix} \begin{bmatrix} 1 & -4 \\\ -4 & -5 \end{bmatrix} \begin{bmatrix} 2 \\\ -2 \end{bmatrix} = 16\]

• $Q(\mathbf{x})$ function 에 대입한 결과 16이라는 값이 도출됨을 확인할 수 있다. 마찬가지로 $\mathbf{y} = P^T\mathbf{x}$ 를 계산하여 구하면

\[\mathbf{y} = P^T\mathbf{x} = \begin{bmatrix} 2/\sqrt{5} & -1/\sqrt{5} \\\ 1/\sqrt{5} & 2/\sqrt{5} \end{bmatrix} \begin{bmatrix} 2 \\\ -2 \end{bmatrix} = \begin{bmatrix} 6/\sqrt{5} \\\ -2/\sqrt{5} \end{bmatrix}\]

• $\mathbf{y}$ 의 값을 우리가 change of variable 을 통해 나온 식에 대입해보면

\[3y_1^2 - 7y_2^2 = 3(6/\sqrt{5})^2 - 7(-2/\sqrt{5})^2 = 16\]

• quadratic form 의 값을 구하든 chagne of varialbe 을 적용하여 값을 구하든 두 방법의 결과가 동일하다는 것을 확인할 수 있다.

• $Q(\mathbf{x})$ 를 하게 되면 $\mathbb{R}^n$ space 에서 $\mathbb{R}$ space 의 하나의 값으로 가게된다.
• 원래라면 $\mathbf{x}^TA\mathbf{x}$ 처럼 cross-product 가 있는 형태로 16이라는 값을 도출했지만
• change of variable 인 $\mathbf{y}^TD\mathbf{y}$ 으로 cross-product 없이 quadratic form 을 전개할 수도 있다라고 이해하면 된다.

The Principal Axes Theorem - 주축 정리

Theorem4. The Principal Axes Theorem

Let $A$ be an $n \times n$ symmetric matrix. Then there is an orthogonal change of variable, $\; \mathbf{x} = P\mathbf{y} \;$ , that transforms the quadratic form $\; \mathbf{x}^TA\mathbf{x}\;$ into a quadratic form $\; \mathbf{y}^TD\mathbf{y}\;$ with no cross-product term.

• 위 예제에서 본 것을 정리한 것이다.

• $A$ 행렬이 $n \times n$ 인 symmetric matrix 라고 가정하면 quadratic form 인 $Q(\mathbf{x}) = \mathbf{x}^TA\mathbf{x}$ 에서 $\mathbf{x} = P\mathbf{y}$ 를 대입하여 $\mathbf{y}^TD\mathbf{y}$ 로 변경하면 cross-product term 이 사라진다.

• $A$ 행렬의 eigenvector 로 이루어진 $P$ 행렬을 quadratic form 의 principal axes 라고 부른다.

A Geometric View of Principal Axes - 주축의 기하학적 시점

• 주축을 기하학적 관점으로 보면 편리하점이 있다는 것을 확인할 수 있다.

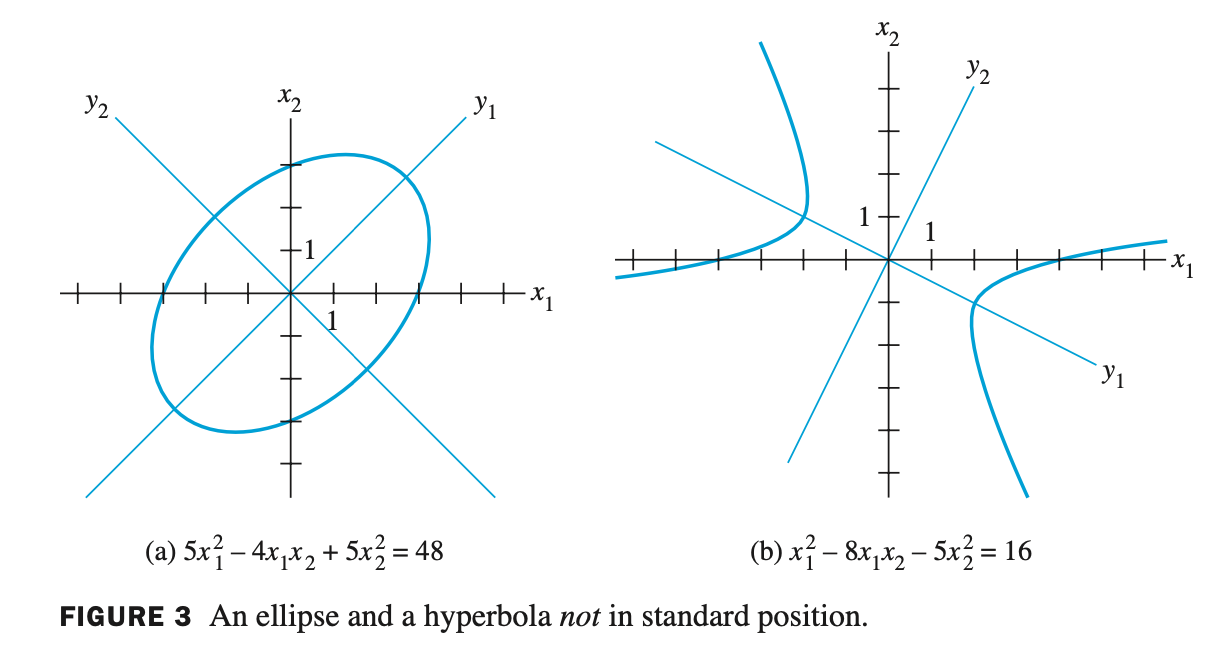
• 특히 quadratic form 에서 cross-product term 이 존재하는 경우 그래프를 그리기 매우 힘들다. 따라서 principal axes 를 구해서 그래프를 그리면 매우 쉬워진다.

• (1) $\quad$ cross-product term 이 없는 ellipse(타원) 와 hyperbola(쌍곡선) 를 그려보면

• (2) $\quad$ cross-product term 이 있는 경우 ellipse(타원) 와 hyperbola(쌍곡선) 를 그려보면

• principal axes $y_1, y_2$ 를 기준으로 두고 ellipse 와 hyperbola 를 그리면 일반적인 ellipse 와 hyperbola 처럼 쉽게 그릴 수 있다.

Classifying Quadratic Form - 이차 형식 분류하기

• quadratic form 을 용어적으로 몇 가지로 구분할 수 있다.
• $Q(\mathbf{x}) = \mathbf{x}^TA\mathbf{x} $ is a real-valued function with domain $\mathbb{R}^n$
• $Q(\mathbf{x})$ 는 real value 인 단일 값으로 보내는 함수이다.

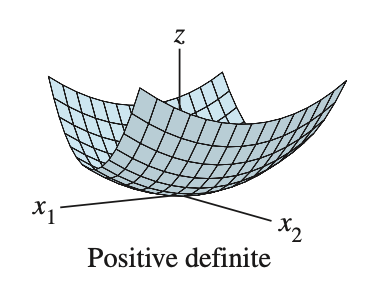
positive definite if \(Q(\mathbf{x}) > 0\) for all \(\mathbf{x} \ne 0\)

• $\mathbf{x} = \mathbf{0}$ 0 벡터인 경우를 제외하고 모든 $Q(\mathbf{x})$ 가 양수이면 positive definite 이라고 한다.

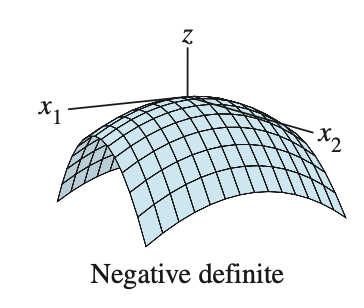
negative definite if \(Q(\mathbf{x}) < 0\) for all \(\mathbf{x} \ne 0\)

• $\mathbf{x} = \mathbf{0}$ 0 벡터인 경우를 제외하고 모든 $Q(\mathbf{x})$ 가 음수이면 negative definite 이라고 한다.

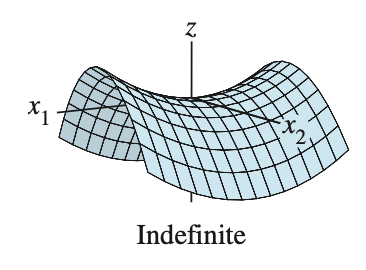
indefinite definite if \(Q(\mathbf{x})\) assumes both positive and negative values

• $Q(\mathbf{x})$ 가 양수와 음수 모두 지니고 있으면 indefinite definite 이라고 한다.

positive semidefinite if \(Q(\mathbf{x}) \ge 0\) for all $\mathbf{x}$

• 모든 $\mathbf{x}$ 에 대해 $Q(\mathbf{x}) \ge 0$ 이면 positive semidefinite 이다.

negative semidefinite if \(Q(\mathbf{x}) \le 0\) for all $\mathbf{x}$

• 모든 $\mathbf{x}$ 에 대해 $Q(\mathbf{x}) \le 0$ 이면 neagtive semidefinite 이다.

Quadratic Forms and Eigenvaleus - 이차 형식과 고유치

Theorem5. Quadratic Forms and Eigenvalues

Let $A$ be an $n \times n$ symmetric matrix. Then a quadratic form $\; \mathbf{x}^TA\mathbf{x} \;$ is :

a.  positive definite if and only if the eigenvaleus of $A$ are all positive,
b.  negative definite if and only if the eigenvalues of $A$ are all negative,
c.  indefinite if and only if $A$ has both positive and negative eigenvalues.

• 증명
• theorem4 the principal axes theorem 에 의해 quadratic form 을 나타내면 다음과 같다.

\[Q(\mathbf{x}) = \mathbf{x}^TA\mathbf{x} = \mathbf{y}^TD\mathbf{y} = \lambda _1y_1^2 + \lambda _2y_2^2 + \dots + \lambda _ny_n^2\]

• 여기서 $y_n^2$ 은 제곱 형태이므로 모두 양수이다.
• 따라서 $\lambda$ (eigenvalue 고유치) 에 의해 quadratic form 의 부호가 결정된다.

Example 4

Is $Q(\mathbf{x}) = 3x_1^2 + 2x_2^2 + x_3^2 + 4x_1x_2 + 4x_2x_3 $ positive definite?

• quadratic form 을 matrix 형태로 나타내면 다음과 같다.

\[A = \begin{bmatrix} 3 & 2 & 0 \\\ 2 & 2 & 2 \\\ 0 & 2 & 1 \end{bmatrix}\]

• 이후 characteristic equation 을 통해 eigenvalue, eigenvector 를 구하면 다음과 같다.

\[A - \lambda I = \begin{bmatrix} 3 - \lambda & 2 & 0 \\\ 2 & 2 - \lambda & 2 \\\ 0 & 2 & 1 - \lambda \end{bmatrix}\] \[\mbox{det} (A - \lambda I) = (3-\lambda) \begin{bmatrix} 2 - \lambda & 2 \\\ 2 & 1 -\lambda \end{bmatrix} - 2 \begin{bmatrix} 2 & 2 \\\ 0 & 1-\lambda \end{bmatrix} + 0\] \[= (2-\lambda)(\lambda + 1)(\lambda - 5) = 0\]

• 여기서 eigenvalue 가 2, -1, 5 양수와 음수가 섞여있으므로 indefinite quadratic form 으로 구분할 수 있다.

• 번외로 일반적으로 컴퓨터로 계산할 때 모든 eigenvalue 를 찾기 위해서는 QR 알고리즘을 사용하여 definite 를 판단하는데 QR 알고리즘 보다 훨씬 덜 무겁고 효율적인 알고리즘인 Cholesky factorization 가 존재한다.

\[A = R^TR \; \mbox{or} \; A = LL^T\]

• 여기서 $R$ 은 upper triangular matrix 를 표현하고, $L$ 은 lower triangular matrix 를 표현한다.