Hits

용어 정리

  • The best approximation therorem - 최고 근사 정리


Desktop View

  • orthogonal projection 에 대해 복습을 해보자.
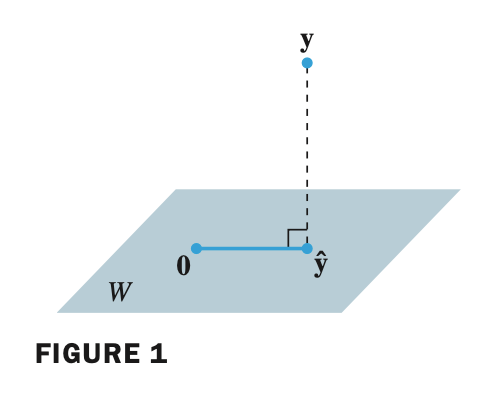
  • 벡터 $\mathbf{y}$ 와 subspace $W$ 가 주어졌을 때, $\mathbf{y}$ 를 서로 직교하는 두 개의 벡터 합으로 분해할 수 있다.
\[\mathbf{y} = \widehat{\mathbf{y}} + \mathbf{z}\]
  • 여기서 $\widehat{\mathbf{y}}$ 은 $W$ subspace 안에 있으며 다음과 같이 구할 수 있다.
\[\widehat{\mathbf{y}} = \mbox{proj}_L\mathbf{y} = {\mathbf{y} \cdot \mathbf{u} \over \mathbf{u} \cdot \mathbf{u}} \mathbf{u}\]


  • 이전 포스팅에서 살펴본 orthogonal projection 은 $\mathbb{R}^n$ space 에 속한 벡터간의 orthogonal projection 에 대해서 살펴봤었다.
  • 다음 내용은 subspace 에 orthogonal projection 을 하는 방법에 대해 알아볼 것이다.



Theorem8. The Orthogonal Decomposition Theorem

Let $W$ be a subspace of $\mathbb{R}^n$ . Then each $\mathbf{y}$ in $\mathbb{R}^n$ can be written uniquely in the form

\[\mathbf{y} = \widehat{\mathbf{y}} + \mathbf{z}\]

where $\widehat{\mathbf{y}}$ is in $W$ and $\mathbf{z}$ is in $W^{\perp}$ . In fact, if {$\mathbf{u}_1 , \dots , \mathbf{u}_p$} is any orthogonal basis of $W$ , then

\[\widehat{\mathbf{y}} = {\mathbf{y} \cdot \mathbf{u}_1 \over \mathbf{u}_1 \cdot \mathbf{u}_1} \mathbf{u}_1 + \dots + {\mathbf{y} \cdot \mathbf{u}_p \over \mathbf{u}_p \cdot \mathbf{u}_p} \mathbf{u}_p\]

and $\mathbf{z} = \mathbf{y} - \widehat{\mathbf{y}}$ .

  • 벡터 $\mathbf{y}$ 를 두 개의 벡터로 분해(decomposition) 할 수 있으며, $\widehat{\mathbf{y}}$ 은 $W$ subspace 안에 존재하고 $\mathbf{z}$ 는 $W^{\perp}$ 에 존재한다.
  • 만약 {$\mathbf{u}_1 , \dots , \mathbf{u}_p$} 가 orthogonal basis (직교 기저) 이면 $\widehat{\mathbf{y}}$ 은 $\mathbf{u}$ 의 linear combination 형태로 표현할 수 있고 각각의 weight(가중치)는 다음과 같이 표현할 수 있다.
\[\widehat{\mathbf{y}} = {\mathbf{y} \cdot \mathbf{u}_1 \over \mathbf{u}_1 \cdot \mathbf{u}_1} \mathbf{u}_1 + \dots + {\mathbf{y} \cdot \mathbf{u}_p \over \mathbf{u}_p \cdot \mathbf{u}_p} \mathbf{u}_p\]
  • 그리고 $\mathbf{z}$ 는 $\widehat{\mathbf{y}}$ 에 직교하며, $\mathbf{y} - \widehat{\mathbf{y}}$ 으로 나타낼 수 있다.

Desktop View

  • 만약 $\mathbf{y}$ 가 $W$ 에 존재할 때, $\mathbf{y}$ 를 $W$ 에 proection 하면 $\mathbf{y}$ 가 나온다.
  • 위 내용을 좀 더 풀어서 쓰면, 위에서 {$\mathbf{u}_1 , \dots , \mathbf{u}_p$} is orthogonal basis of $W$ 이므로 linear combination 형태로 나타내면 다음과 같다.
\[\widehat{\mathbf{y}} = c_1\mathbf{u}_1 + \dots + c_p\mathbf{u}_p\]
  • 이미 $\mathbf{u}_1$ 은 $W$ 의 orthogonal basis 이므로 $\mathbf{z}$ 와 perpendicular 하므로 $\mathbf{z} \cdot \mathbf{u}_1$ 은 0이된다.
\[\mathbf{y} \cdot \mathbf{u}_1 = (\widehat{\mathbf{y}} + \mathbf{z}) \cdot \mathbf{u}_1 = \widehat{\mathbf{y}} \cdot \mathbf{u}_1 + \mathbf{z} \cdot \mathbf{u}_1 = \widehat{\mathbf{y}} \cdot \mathbf{u}_1 = c_1\mathbf{u}_1 \cdot \mathbf{u}_1\]
  • 이를 weight 를 기준으로 정리 및 일반화하면 다음과 같다.
\[c_1 = {\mathbf{y} \cdot \mathbf{u}_1 \over \mathbf{u}_1 \cdot \mathbf{u}_1} \quad \quad c_j = { \mathbf{y} \cdot \mathbf{u}_j \over \mathbf{u}_j \cdot \mathbf{u}_j}\]
  • 결론은 벡터 $\mathbf{y}$ 를 $W$ 라는 subspace 에 orthogonal projection 한 벡터가 $\widehat{\mathbf{y}}$ 으로 주어졌으면
  • $\widehat{\mathbf{y}}$ 이랑 subspace 내의 임의의 $\mathbf{u}_j$ 와 dot product 를 한 것과 $\mathbf{y}$ 를 마찬가지로 subspace 내의 임의의 $\mathbf{u}_j$ 와 dot product 를 한 것과 같다라는 의미이다.
\[\mathbf{y} \cdot \mathbf{u}_j = \widehat{\mathbf{y}} \cdot \mathbf{u}_j\]


Example 1
Let $\mathbf{u}_1 = (2, 5, -1) \;, \; \mathbf{u}_2 = (-2, 1, 1) $ , and $ \mathbf{y} = (1, 2, 3) $ . {$\mathbf{u}_1, \mathbf{u}_2$} is an orthogonal basis for $W = $ Span {$\mathbf{u}_1, \mathbf{u}_2$}. Write $\mathbf{y}$ as the sum of a vector in $W$ and a vector orthogonal $W$ .

  • $W$ 의 orthogonal basis 인 $\mathbf{u}_1, \mathbf{u}_2$ 와 $\mathbf{y}$ 가 주어졌을 때, \mathbf{y} 를 $W$ 에 있는 벡터와 $W$ 와 직교하는 벡터의 합으로 분해하는 문제이다.
  • 즉 $\mathbf{y} = \widehat{\mathbf{y}} + \mathbf{z} $ 형태로 나타내는 것
\[\mathbf{u}_1 = \begin{bmatrix} \phantom{-}2 \\\ \phantom{-}5 \\\ -1 \end{bmatrix} \; , \quad \mathbf{u}_2 = \begin{bmatrix} -2 \\\ \phantom{-}1 \\\ \phantom{-}1 \end{bmatrix} \; , \quad \mathbf{y} = \begin{bmatrix} 1 \\\ 2 \\\ 3 \end{bmatrix}\] \[\widehat{\mathbf{y}} = {\mathbf{y} \cdot \mathbf{u}_1 \over \mathbf{u}_1 \cdot \mathbf{u}_1} \mathbf{u}_1 + {\mathbf{y} \cdot \mathbf{u}_2 \over \mathbf{u}_2 \cdot \mathbf{u}_2} \mathbf{u}_2 = { 9 \over 30 } \begin{bmatrix} \phantom{-}2 \\\ \phantom{-}5 \\\ -1 \end{bmatrix} + {3 \over 6} \begin{bmatrix} -2 \\\ 1 \\\ 1 \end{bmatrix} = \begin{bmatrix} -2 / 5 \\\ 2 \\\ 1 / 5 \end{bmatrix}\] \[\mathbf{y} - \widehat{\mathbf{y}} = \begin{bmatrix} 1 \\\ 2 \\\ 3 \end{bmatrix} - \begin{bmatrix} -2 / 5 \\\ 2 \\\ 1/5 \end{bmatrix} = \begin{bmatrix} 7 / 5 \\\ 0 \\\ 14 / 5 \end{bmatrix}\] \[\mathbf{y} = \begin{bmatrix} -2/5 \\\ 2 \\\ 1/5 \end{bmatrix} + \begin{bmatrix} 7/5 \\\ 0 \\\ 14/5 \end{bmatrix}\]



A geometric interpretation of the Orthogonal Projection - 정사영의 기하학적 해석

  • 벡터 $\mathbf{y}$ 를 2차원 평면인 subspace $W$ 에 projection 한다고 생각해보자.
  • $W$ 는 orthogonal basis $\mathbf{u}_1, \mathbf{u}_2$ 가 Span 한다고 할 때, $\mathbf{y}$ 를 subspace $W$ 에 projection 하는 방법은 각각의 orthogonal basis 에 projection 해준 것을 더해주면 된다.

Desktop View

  • $\widehat{\mathbf{y}}_1$ 은 $\mathbf{u}_1$ 에 projection 한 것이고
  • $\widehat{\mathbf{y}}_2$ 는 $\mathbf{u}_2$ 에 projection 한 것이다.



Theorem9. The best approximation theorem

Let $W$ be a subspace of $\mathbb{R}^n$ , let $\mathbf{y}$ be any vector in $\mathbb{R}^n$ , and let $\widehat{\mathbf{y}}$ be the orthogonal projection of $\mathbf{y}$ onto $W$ . Then $\widehat{\mathbf{y}}$ is the closest point in $W$ to $\mathbf{y}$ , in the sense that

\[\lVert \mathbf{y} - \widehat{\mathbf{y}} \rVert < \lVert \mathbf{y} - \mathbf{v} \rVert\]

for all $\mathbf{v}$ in $W$ distinct from $\widehat{\mathbf{y}}$ .

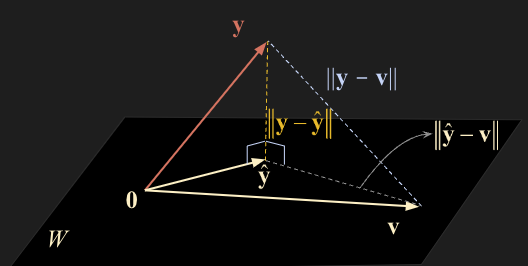
  • 특정 벡터 $\mathbf{y}$ 와 subspace $W$ 간의 제일 짧은 거리를 구하는 정리이다. $\mathbf{y}$ 를 $W$ 에 projection 한 $\widehat{\mathbf{y}}$ 이 제일 가까운 거리이다.

  • 증명

Desktop View

  • subspace $W$ 상의 임의의 벡터 $\mathbf{v}$ 를 가정하고 특정 벡터 $\mathbf{y}$ 사이의 distance를
  • 벡터 $\mathbf{y}$ 와 subspace $W$ 사이의 가장 짧은 distance $\mathbf{y} - \widehat{\mathbf{y}}$ 와 $\widehat{\mathbf{y}}$ 과 임의의 벡터 $\mathbf{v}$ 사이의 distance를 나타내는 $\widehat{\mathbf{y}} - \mathbf{v}$ distance의 합으로 표현할 수 있다.
\[\mathbf{y} - \mathbf{v} = (\mathbf{y} - \widehat{\mathbf{y}}) + (\widehat{\mathbf{y}} - \mathbf{v})\]
  • 위 그림을 보면 $\mathbf{y} - \widehat{\mathbf{y}}$ 와 $\widehat{\mathbf{y}} - \mathbf{v}$ 는 서로 orthogonal 한 관계에 있으므로
  • 우리는 피타고라스의 정리를 적용시킬 수 있다. 그림으로 봐도 삼각형의 형태가 눈에 보일 것이다.
\[{\lVert \mathbf{y} - \mathbf{v} \rVert}^2 = {\lVert \mathbf{y} - \widehat{\mathbf{y}} \rVert}^2 + {\lVert \widehat{\mathbf{y}} - \mathbf{v} \rVert}^2\]
  • 여기서 주의할 것은, $\widehat{\mathbf{y}} - \mathbf{v}$ 은 서로 다른 벡터이기 때문에 nonzero 이고 따라서 ${\lVert \widehat{\mathbf{y}} - \mathbf{v} \rVert}^2$ 는 항상 양수의 값을 갖는다.
  • 따라서 다음과 같은 성질을 만족한다.
\[\lVert \mathbf{y} - \widehat{\mathbf{y}} \rVert < \lVert \mathbf{y} - \mathbf{v} \rVert\]


Example 2
Let $\mathbf{u}_1 = (5, -2, 1) \; , \; \mathbf{u}_2 = (1, 2, -1) \; , \; \mathbf{y} = (-1, -5, 10) \; , \; $ and $W = $ Span {$\mathbf{u}_1, \mathbf{u}_2$}. Find the distance from $\mathbf{y}$ to $W$ .

\[\widehat{\mathbf{y}} = {\mathbf{y} \cdot \mathbf{u}_1 \over \mathbf{u}_1 \cdot \mathbf{u}_1} \mathbf{u}_1 + {\mathbf{y} \cdot \mathbf{u}_2 \over \mathbf{u}_2 \cdot \mathbf{u}_2} \mathbf{u}_2\] \[= { (-1, -5, 10 ) \cdot (5, -2, 1) \over (5, -2, 1) \cdot (5, -2, 1) } \mathbf{u}_1 + { (-1, -5, 10 ) \cdot (1, 2, -1) \over (1, 2, -1) \cdot (1, 2, -1) } \mathbf{u}_2\] \[= {15 \over 30} \begin{bmatrix} \phantom{-}5 \\\ -2 \\\ \phantom{-}1 \end{bmatrix} + {-21 \over 6} \begin{bmatrix} \phantom{-}1 \\\ \phantom{-}2 \\\ -1 \end{bmatrix} = \begin{bmatrix} -1 \\\ -8 \\\ \phantom{-}4 \end{bmatrix}\] \[\mathbf{y} - \widehat{\mathbf{y}} = \begin{bmatrix} -1 \\\ -5 \\\ 10 \end{bmatrix} - \begin{bmatrix} -1 \\\ -8 \\\ \phantom{-}4 \end{bmatrix} = \begin{bmatrix} 0 \\\ 3 \\\ 6 \end{bmatrix}\] \[\lVert \mathbf{y} - \widehat{\mathbf{y}} \rVert = \sqrt{3^2 + 6^2} = \sqrt{45} = 3\sqrt{5}\]



Theorem10.

If {$\mathbf{u}_1 , \dots , \mathbf{u}_p$} is an orthonormal basis for a subspace $W$ of $\mathbb{R}^n$ , then

\[\mbox{proj}_W \mathbf{y} = (\mathbf{y} \cdot \mathbf{u}_1) \mathbf{u}_1 + (\mathbf{y} \cdot \mathbf{u}_2) \mathbf{u}_2 + \dots + (\mathbf{y} \cdot \mathbf{u}_p) \mathbf{u}_p\]

If $U = [ \mathbf{u}_1 \quad \mathbf{u}_2 \quad \dots \quad \mathbf{u}_p ]$ , then

\[\mbox{proj}_W \mathbf{y} = UU^T \mathbf{y} \quad \quad \mbox{for all} \; \mathbf{y} \; \mbox{in} \; \mathbb{R}^n\]
  • {$\mathbf{u}_1 , \dots , \mathbf{u}_p$} 가 $W$ 에 대한 orthonormal basis 일 때, $\mathbf{y}$ 를 $W$ 에 projection 한 것은 다음과 같이 표현할 수 있다.
\[\mbox{proj}_W \mathbf{y} = (\mathbf{y} \cdot \mathbf{u}_1) \mathbf{u}_1 + (\mathbf{y} \cdot \mathbf{u}_2) \mathbf{u}_2 + \dots + (\mathbf{y} \cdot \mathbf{u}_p) \mathbf{u}_p\]
  • 여기서 weight 들인 $(\mathbf{y} \cdot \mathbf{u}_1) , (\mathbf{y} \cdot \mathbf{u}_2) , \dots , (\mathbf{y} \cdot \mathbf{u}_p)$ 들은 다음과 같이 $\mathbf{u}_1^T\mathbf{y}, \mathbf{u}_2^T\mathbf{y}, \dots , \mathbf{u}_p^T\mathbf{y}$ Transpose 형태로 나타낼 수 있다.
\[\mbox{proj}_W \mathbf{y} = (\mathbf{u}_1^T\mathbf{y}) \mathbf{u}_1 + (\mathbf{u}_2^T\mathbf{y}) \mathbf{u}_2 + \dots + (\mathbf{u}_p^T\mathbf{y}) \mathbf{u}_p\] \[= \begin{bmatrix} \mathbf{u}_1 & \dots & \mathbf{u}_p \end{bmatrix} \begin{bmatrix} \mathbf{u}_1^T\mathbf{y} \\\ \vdots \\\ \mathbf{u}_p^T\mathbf{y} \end{bmatrix} = \begin{bmatrix} \mathbf{u}_1 & \dots & \mathbf{u}_p \end{bmatrix} \begin{bmatrix} \mathbf{u}_1^T \\\ \vdots \\\ \mathbf{u}_p^T \end{bmatrix} \mathbf{y} = \begin{bmatrix} \mathbf{u}_1 & \dots & \mathbf{u}_p \end{bmatrix} {\begin{bmatrix} \mathbf{u}_1 & \dots & \mathbf{u}_p \end{bmatrix}}^T \mathbf{y} = UU^T \mathbf{y}\]