---

용어 정리

• Orthogonal Sets - 직교 집합
• Orthogonal Basis - 직교 기저
• Orthogonal Projection - 정사영
• Orthonormal Sets - 정규 직교 집합

Orthogonal Sets - 직교 집합

• 벡터의 집합 {$\mathbf{u}_1 , \dots , \mathbf{u}_p$} 이 존재할 때, 집합의 모든 벡터 쌍이 orthogonal(직교)이면 orthogonal set(직교 집합) 이라고 한다.
• 즉, $\mathbf{u}_i \cdot \mathbf{u}_j = 0$ 이다.

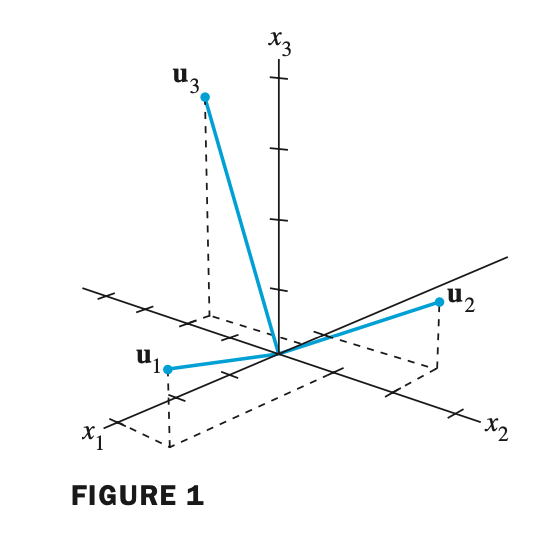
• 직교 집합 {$\mathbf{u}_1 , \mathbf{u}_2 , \mathbf{u}_3$} 이 주어졌을 때, 각각의 벡터를 내적해보자

\[\mathbf{u}_1 = \begin{bmatrix} 3 \\\ 1 \\\ 1 \end{bmatrix} \; , \quad \mathbf{u}_2 = \begin{bmatrix} -1 \\\ \phantom{-}2 \\ \phantom{-}1 \end{bmatrix} \; , \quad \mathbf{u}_3 = \begin{bmatrix} -1/2 \\\ -2 \\\ 7/2 \end{bmatrix}\]

\[\mathbf{u}_1 \cdot \mathbf{u}_2 = 3(-1) + 1(2) + 1(1) = 0\] \[\mathbf{u}_1 \cdot \mathbf{u}_3 = 3(-{1 \over 2}) + 1(-2) + 1({7 \over 2}) = 0\] \[\mathbf{u}_2 \cdot \mathbf{u}_3 = -1(-{1 \over 2}) + 2(-2) + 1({7 \over 2}) = 0\]

• 이처럼 각각의 벡터 쌍의 내적은 0이 된다.

Theorem4.

If $ S = $ {$ \mathbf{u}_1 , \dots , \mathbf{u}_p $} is an orthogonal set of nonzero vectors in $\mathbb{R}^n$ , then $S$ is linearly independent and hence is a basis for the subspace spanned by $S$ .

• $S$ 가 nonzero 벡터들의 orthogonal set 이면 $S$ 는 linearly independent 하고, orthogonal set 은 $S$ 를 Span 하는 basis(기저) 이다.

• 증명
• $S$ 의 orthogonal set 의 linear combination 이 0이라고 가정하자.

\[\mathbf{0} = c_1\mathbf{u}_1 + \dots + c_p\mathbf{u}_p\]

• 양변에 $\mathbf{u}_1$ 을 내적해주자.

\[0 = \mathbf{0} \cdot \mathbf{u}_1 = ( c_1\mathbf{u}_1 + \dots + c_p\mathbf{u}_p) \cdot \mathbf{u}_1\] \[= (c_1\mathbf{u}_1) \cdot \mathbf{u}_1 + (c_2\mathbf{u}_2) \cdot \mathbf{u}_1 + \dots + (c_p\mathbf{u}_p) \cdot \mathbf{u}_1\]

• 서로 다른 벡터의 내적은 직교이므로 0이 된다.

\[= c_1(\mathbf{u}_1 \cdot \mathbf{u}_1) + c_2(\mathbf{u}_2 \cdot \mathbf{u}_1) + \dots + c_p(\mathbf{u}_p \cdot \mathbf{u}_1)\] \[= c_1(\mathbf{u}_1 \cdot \mathbf{u}_1)\]

• 여기서 $\mathbf{u}_1$ 은 nonzero 이므로 $c_1 = 0$ 이 되어야 식이 성립한다.
• 이것을 모든 벡터에 적용하면 $c_1 , \dots , c_p = 0$ 이다. 이는 trivial solution(자명해) 이므로 $S$ 의 orthogonal set 은 linearly independent 가 된다.

Orthogonal Basis - 직교 기저

An orthogonal basis for a subspace $W \;$ of $\mathbb{R}^n$ is a basis for $W \;$ that is also an orthogonal set.

• subspace $W$ 에 대한 orthogonal basis 는 $W$ 에 대한 basis 이고 orthogonal set 이다.

• 각각의 basis 가 서로 perpendicular, orthogonal 하다는 의미이다.

• orthogonal basis 를 통해 매우 간단하게 weight 의 solution 을 구할 수있다.
• 특히 augmented matrix 로 만들어서 row reduction 을 하는 복잡한 계산을 안해도 되는데 이는 theorem 5 에서 이어지는 내용이다.

Theorem5.

Let {$ \mathbf{u}_1 , \dots , \mathbf{u}_p $} be an orthogonal basis for a subspace $W \;$ of $\mathbb{R}^n \;$ . For each $\mathbf{y} \;$ in $W \;$ , the weights in the linear combination

\[\mathbf{y} = c_1\mathbf{u}_1 + \dots + c_p\mathbf{u}_p\]

are given by

\[c_j = {\mathbf{y} \cdot \mathbf{u}_j \over \mathbf{u}_j \cdot \mathbf{u}_j} \quad \quad (j = 1 , \dots , p)\]

• $W$ 에 대한 orthogonal basis 가 주어졌을 때, $W$ 에 존재하는 임의의 벡터 $\mathbf{y}$ 를 orthogonal basis 의 linear combination 형태로 나타내면 다음과 같이 가중치(weight)가 주어진다.

\[\mathbf{y} = c_1\mathbf{u}_1 + \dots + c_p\mathbf{u}_p\]

• 이전에는 가중치를 찾기 위해서 row reduction 을 통해 가중치의 해를 찾았는데, orthogonal basis 인 경우 다음과 같은 가중치 공식이 주어져 보다 쉽고 간편하게 계산이 가능하다.

\[c_j = {\mathbf{y} \cdot \mathbf{u}_j \over \mathbf{u}_j \cdot \mathbf{u}_j} \quad \quad (j = 1 , \dots , p)\]

• 증명
• 위 선형 결합 식에서 양변에 $\mathbf{u}_1$ 을 내적해주자.

\[\mathbf{y} \cdot \mathbf{u}_1 = (c_1\mathbf{u}_1 + \dots + c_p\mathbf{u}_p) \cdot \mathbf{u}_1 = c_1(\mathbf{u}_1 \cdot \mathbf{u}_1)\]

• $\mathbf{u}_1 , \dots , \mathbf{u}_p$ 는 직교하므로 서로 내적하면 0이 나온다. 따라서 $c_1(\mathbf{u}_1 \cdot \mathbf{u}_1)$ 만 남게 된다.
• 이를 $c$ 에 대한 식으로 정리하면 다음과 같이 도출된다.

\[c_j = {\mathbf{y} \cdot \mathbf{u}_j \over \mathbf{u}_j \cdot \mathbf{u}_j}\]

Example 1

Let $ \; \mathbf{u}_1 = (3, 1, 1) \; , \; \mathbf{u}_2 = (-1, 2, 1) \; \mbox{and} \; \mathbf{u}_3 = (-1/2, -2, 7/2) $ , then the set $ \; S = $ {$\mathbf{u}_1, \mathbf{u}_2, \mathbf{u}_3$} is an orthogonal basis for $\mathbb{R}^n$ . Express the vector $ \mathbf{y} = (6, 1, -8) $ as a linear combination of the vectors in $S$ .

\[\mathbf{u}_1 = \begin{bmatrix} 3 \\\ 1 \\\ 1 \end{bmatrix} \; , \quad \mathbf{u}_2 = \begin{bmatrix} -1 \\\ \phantom{-}2 \\\ \phantom{-}1 \end{bmatrix} \; , \quad \mathbf{u}_3 = \begin{bmatrix} -1/2 \\\ -2 \\\ 7/2 \end{bmatrix}\]

\[\mathbf{y} = \begin{bmatrix} \phantom{-}6 \\\ \phantom{-}1 \\\ -8 \end{bmatrix}\]

\[\mathbf{y} \cdot \mathbf{u}_1 = 11 \; , \quad \mathbf{y} \cdot \mathbf{u}_2 = -12 \; , \quad \mathbf{y} \cdot \mathbf{u}_3 = -33\] \[\mathbf{u}_1 \cdot \mathbf{u}_1 = 11 \; , \quad \mathbf{u}_2 \cdot \mathbf{u}_2 = 6 \; , \quad \mathbf{u}_3 \cdot \mathbf{u}_3 = 33 / 2\]

\[\mathbf{y} = {\mathbf{y} \cdot \mathbf{u}_1 \over \mathbf{u}_1 \cdot \mathbf{u}_1 } \mathbf{u}_1 + {\mathbf{y} \cdot \mathbf{u}_2 \over \mathbf{u}_2 \cdot \mathbf{u}_2 } \mathbf{u}_2 + {\mathbf{y} \cdot \mathbf{u}_3 \over \mathbf{u}_3 \cdot \mathbf{u}_3 } \mathbf{u}_3\] \[= {11 \over 11} \mathbf{u}_1 + { -12 \over 6 } \mathbf{u}_2 + { -33 \over 33 / 2 } \mathbf{u}_3\] \[= \mathbf{u}_1 - 2\mathbf{u}_2 - 2\mathbf{u}_3\]

Orthogonal Projection - 정사영

• orthogonal basis {$\mathbf{u}_1 , \dots , \mathbf{u}_n$}이 주어지고, orthogonal basis의 linear combination 으로 표현되는 백터 $\mathbf{y}$ 가 주어졌다고 가정하자.
• 이 때, 벡터 $\mathbf{y}$ 를 두 개의 직교 벡터의 linear combination 으로 분해하는 문제를 고려할 때, 다음과 같이 적을 수 있다.

\[\mathbf{y} = \widehat{\mathbf{y}} + \mathbf{z}\] \[\widehat{\mathbf{y}} = \alpha \mathbf{u}\] \[\mathbf{z} \; \mbox{is some vector orthogonal to } \mathbf{u}\] \[\mathbf{z} = \mathbf{y} - \alpha \mathbf{u}\]

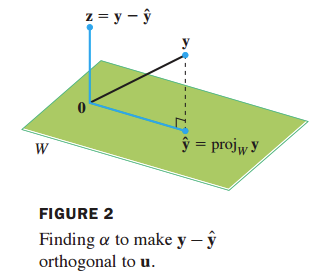
• 그림으로 표시하면 다음과 같다.

• $\mathbf{z}$ 와 $\widehat{\mathbf{y}}$ 는 직교하므로 내적은 0이다.

\[0 = (\mathbf{y} - \alpha \mathbf{u}) \cdot \mathbf{u} = \mathbf{y} \cdot \mathbf{u} - (\alpha \mathbf{u}) \cdot \mathbf{u} = \mathbf{y} \cdot \mathbf{u} - \alpha (\mathbf{u} \cdot \mathbf{u})\]

• 이 때, $\alpha$ 는 다음과 같이 구할 수 있다.

\[\alpha = { \mathbf{y} \cdot \mathbf{u} \over \mathbf{u} \cdot \mathbf{u} }\]

• 따라서 $\widehat{\mathbf{y}}$ 는 다음과 같이 된다.

\[\widehat{\mathbf{y}} = { \mathbf{y} \cdot \mathbf{u} \over \mathbf{u} \cdot \mathbf{u}} \mathbf{u}\]

• 이 $\widehat{\mathbf{y}}$ 을 $\mathbf{u}$ 에 onto 한 $\mathbf{y}$ 의 orthogonal projection (정사영) 이라고 하고, $\mathbf{z}$ 를 $\mathbf{u}$ 에 orthogonal한 $\mathbf{y}$ 의 component 라고 한다.
• 그리고 orthogonal projection 을 다음과 같이 표기할 수 있다.

\[\widehat{\mathbf{y}} = \mbox{proj}_L \; \mathbf{y} = {\mathbf{y} \cdot \mathbf{u} \over \mathbf{u} \cdot \mathbf{u}} \mathbf{u}\]

Example 2
Let $\mathbf{y} = (7, 6)$ and $\mathbf{u} = (4, 2)$ . Find the orthogonal projection of $\mathbf{y}$ onto $\mathbf{u}$ . Then write $\mathbf{y}$ as the sum of two orthogonal vectors, one in Span {$\mathbf{u}$} and one orthogonal to $\mathbf{u}$.

• $\mathbf{y}$ 와 $\mathbf{u}$ 가 주어졌을 때, $\mathbf{y}$ 를 $\mathbf{u}$ 에 orthogonal projection 하고, $\mathbf{y}$ 를 두 개의 직교 벡터의 합으로 표현하는 문제이다.

\[\mathbf{y} = \begin{bmatrix} 7 \\\ 6 \end{bmatrix} \; \mbox{and} \; \mathbf{u} = \begin{bmatrix} 4 \\\ 2 \end{bmatrix}\] \[\mathbf{y} \cdot \mathbf{u} = \begin{bmatrix} 7 \\\ 6 \end{bmatrix} \cdot \begin{bmatrix} 4 \\\ 2 \end{bmatrix} = 40\] \[\mathbf{u} \cdot \mathbf{u} = \begin{bmatrix} 4 \\\ 2 \end{bmatrix} \cdot \begin{bmatrix} 4 \\\ 2 \end{bmatrix} = 20\] \[\widehat{\mathbf{y}} = {\mathbf{y} \cdot \mathbf{u} \over \mathbf{u} \cdot \mathbf{u}} \mathbf{u} = {40 \over 20} \mathbf{u} = 2 \begin{bmatrix} 4 \\\ 2 \end{bmatrix} = \begin{bmatrix} 8 \\\ 4 \end{bmatrix}\] \[\mathbf{y} - \widehat{\mathbf{y}} = \begin{bmatrix} 7 \\\ 6 \end{bmatrix} - \begin{bmatrix} 8 \\\ 4 \end{bmatrix} = \begin{bmatrix} -1 \\\ \phantom{-}2 \end{bmatrix}\]

Example 3
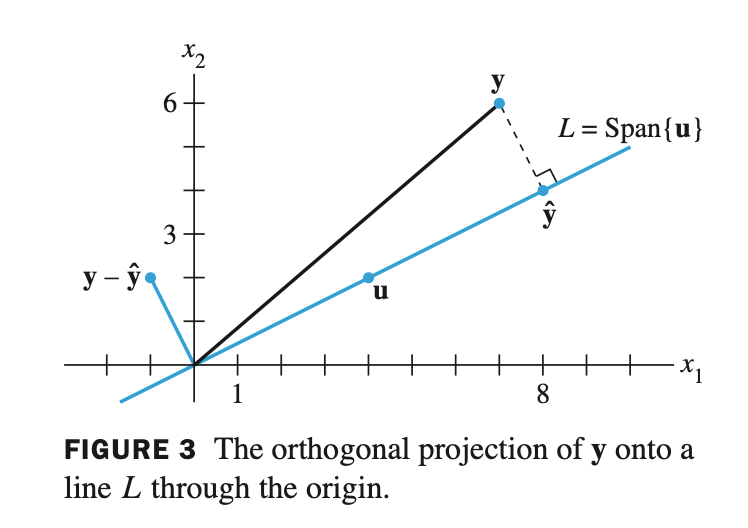
Find the distance from y to Span {$\mathbf{u}$}.

• $\mathbf{y}$ 와 직선 $L$ 의 거리를 구하는 문제이다.
• $\mathbf{y}$ 에 $\widehat{\mathbf{y}}$ 을 빼면 가장 가까운 거리를 구할 수 있다.

\[\lVert \mathbf{y} - \widehat{\mathbf{y}} \rVert = \sqrt{(-1)^2 + 2^2} = \sqrt{5}\]

Orthonormal Set - 정규 직교 집합

• 집합 {$\mathbf{u}_1 , \dots , \mathbf{u}_p$} 가 unit vector 의 orthogonal set 이면 이는 orthonormal set 이라고 부른다.

Example 4
Show that {$\mathbf{v}_1, \mathbf{v}_2, \mathbf{v}_3$} is an orthonormal basis of $\mathbb{R}^n$ , where

\[\mathbf{v}_1 = \begin{bmatrix} 3 / \sqrt{11} \\\ 1 / \sqrt{11} \\\ 1 / \sqrt{11} \end{bmatrix} \; , \quad \mathbf{v}_2 = \begin{bmatrix} -1 / \sqrt{6} \\\ 2 / \sqrt{6} \\\ 1 / \sqrt{6} \end{bmatrix} \; , \quad \mathbf{v}_3 = \begin{bmatrix} -1 / \sqrt{66} \\\ -4 / \sqrt{66} \\\ 7 / \sqrt{66} \end{bmatrix}\]

\[\mathbf{v}_1 \cdot \mathbf{v}_2 = -3 / \sqrt{66} + 2 / \sqrt{66} + 1 / \sqrt{66} = 0\] \[\mathbf{v}_1 \cdot \mathbf{v}_3 = -3 / \sqrt{726} - 4 / \sqrt{726} + 7 / \sqrt{726} = 0\] \[\mathbf{v}_2 \cdot \mathbf{v}_3 = 1 / \sqrt{396} - 8 / \sqrt{396} + 7 / \sqrt{396} = 0\] \[\mathbf{v}_1 \cdot \mathbf{v}_1 = 9 / 11 + 1 / 11 + 1/ 11 = 1\] \[\mathbf{v}_2 \cdot \mathbf{v}_2 = 1 / 6 + 4 / 6 + 1 / 6 = 1\] \[\mathbf{v}_3 \cdot \mathbf{v}_3 = 1 / 66 + 16 / 66 + 49 / 66 = 1\]

• 각 벡터의 길이가 1인 unit vector 이고, 각각의 벡터의 내적이 0 이므로 orthonormal set 임을 확인할 수 있다.

Theorem6.

An $m \times n$ matrix $U$ has orthonormal columns if and only if $ U^TU = I $ .

• $m \times n$ 크기의 행렬 $U$ 가 orthonormal column 들로 이루어져 있으면 $ U^TU = I $ 이다.
• 증명

\[U^TU = \begin{bmatrix} \mathbf{u}^T_1 \\\ \mathbf{u}^T_2 \\\ \mathbf{u}^T_3 \end{bmatrix} \begin{bmatrix} \mathbf{u}_1 & \mathbf{u}_2 & \mathbf{u}_3 \end{bmatrix} = \begin{bmatrix} \mathbf{u}^T_1\mathbf{u}_1 & \mathbf{u}^T_1\mathbf{u}_2 & \mathbf{u}^T_1\mathbf{u}_3 \\\ \mathbf{u}^T_2\mathbf{u}_1 & \mathbf{u}^T_2\mathbf{u}_2 & \mathbf{u}^T_2\mathbf{u}_3 \\\ \mathbf{u}^T_3\mathbf{u}_1 & \mathbf{u}^T_3\mathbf{u}_2 & \mathbf{u}^T_3\mathbf{u}_3 \end{bmatrix}\] \[\mathbf{u}^T_1\mathbf{u}_2 = \mathbf{u}^T_2\mathbf{u}_1 = 0 \; , \quad \mathbf{u}^T_1\mathbf{u}_3 = \mathbf{u}^T_3\mathbf{u}_1 = 0 \; , \quad \mathbf{u}^T_2\mathbf{u}_3 = \mathbf{u}^T_3\mathbf{u}_2 = 0\] \[\mathbf{u}^T_1\mathbf{u}_1 = 1 \; , \quad \mathbf{u}^T_2\mathbf{u}_2 = 1 \; , \quad \mathbf{u}^T_3\mathbf{u}_3 = 1\]

Theorem7.

Let $U$ be an $m \times n$ matrix with orthonormal columns , and let $\mathbf{x}$ and $\mathbf{y}$ be in $\mathbb{R}^n$ , Then

a.  $ \lVert U\mathbf{x} \rVert = \lVert \mathbf{x} \rVert $ b.  $ (U\mathbf{x}) \cdot (U\mathbf{y}) = \mathbf{x} \cdot \mathbf{y} $ c.  $ (U\mathbf{x}) \cdot (U\mathbf{y}) = 0 \quad \mbox{if and only if} \quad \mathbf{x} \cdot \mathbf{y} = 0 $

• $U$ 가 orthonormal column 으로 이루어진 행렬이면 위 3가지 조건을 만족한다.

Example 5
Let $U = \begin{bmatrix} 1 / \sqrt{2} & 2 / 3 \\ 1 / \sqrt{2} & -2 / 3 \\ 0 & 1 / 3 \end{bmatrix} \quad \mbox{and} \quad \mathbf{x} = \begin{bmatrix} \sqrt{2} \\ 3 \end{bmatrix} \; , \; $ Verify $ \; \lVert U\mathbf{x} \rVert = \lVert \mathbf{x} \rVert $ .

\[U\mathbf{x} = \begin{bmatrix} 1 / \sqrt{2} & 2 / 3 \\\ 1 / \sqrt{2} & -2 / 3 \\\ 0 & 1 / 3 \end{bmatrix} \begin{bmatrix} \sqrt{2} \\\ 3 \end{bmatrix} = \begin{bmatrix} \phantom{-}3 \\\ -1 \\\ \phantom{-}1 \end{bmatrix}\] \[\lVert U\mathbf{x} \rVert = \sqrt{9 + 1 + 1} = \sqrt{11}\] \[\lVert \mathbf{x} \rVert = \sqrt{2 + 9} = \sqrt{11}\]

• 이처럼 길이가 같은 것을 확인할 수 있다.