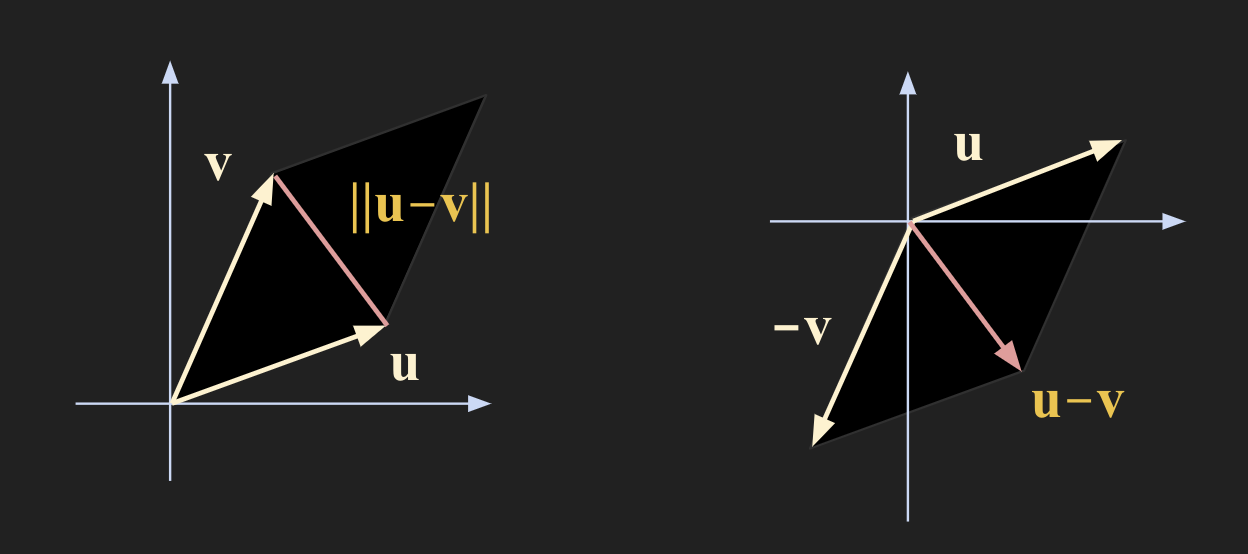Linear Algebra - 5.1 Inner Product And Orthogonality

용어 정리
inner product - 내적
orthogonality - 직교성
perpendicular - 수직
Orthogonal Complements - 직교 여공간

Inner Producjt - 내적

orthogonality 를 알아보기 전에 우선 Inner Product(내적) 을 살펴보자.
다음과 같이 $\mathbb{R}^n$ space 에 두 개의 벡터가 존재한다고 하자.

\[\mathbf{u} = \begin{bmatrix} u_1 \\\ u_2 \\\ \vdots \\\ u_n \end{bmatrix} \quad \mbox{and} \quad \mathbf{v} = \begin{bmatrix} v_1 \\\ v_2 \\\ \vdots \\\ v_n \end{bmatrix}\]

$\mathbf{u}, \mathbf{v}$ 의 내적은 다음과 같다.

\[\begin{bmatrix} u_1 & u_2 & \dots & u_n \end{bmatrix} \begin{bmatrix} v_1 \\\ v_2 \\\ \vdots \\\ v_n \end{bmatrix} = u_1v_1 + u_2v_2 + \dots + u_nv_n\]

위의 식은 $\mathbf{u}^T \cdot \mathbf{v}$ 를 의미한다.
또한 내적의 성질에 따라 $\mathbf{u} \cdot \mathbf{v}$ 는 $\mathbf{v} \cdot \mathbf{u}$ 와 동일하다.

예시 문제
다음 두 벡터의 내적을 구하라.

\[\mathbf{u} = \begin{bmatrix} \phantom{-}2 \\\ -5 \\\ -1 \end{bmatrix} \quad \mbox{and} \quad \mathbf{v} = \begin{bmatrix} \phantom{-}3 \\\ \phantom{-}2 \\\ -3 \end{bmatrix}\] \[\mathbf{u} \cdot \mathbf{v} = \mathbf{u}^T \cdot \mathbf{v} = \begin{bmatrix} 2 & -5 & -1 \end{bmatrix} \begin{bmatrix} \phantom{-}3 \\\ \phantom{-}2 \\\ -3 \end{bmatrix} = (2)(3) + (-5)(2) + (-1)(-3) = -1\] \[\mathbf{v} \cdot \mathbf{u} = \mathbf{v}^T \cdot \mathbf{u} = \begin{bmatrix} 3 & 2 & -3 \end{bmatrix} \begin{bmatrix} \phantom{-}2 \\\ -5 \\\ -1 \end{bmatrix} = (3)(2) + (2)(-5) + (-3)(-1) = -1\]

이처럼 두 벡터의 순서가 바뀌어도 동일하다는 것을 확인할 수 있다.
$\mathbf{u} \cdot \mathbf{v} = \mathbf{v} \cdot \mathbf{u} $

Theorem1.
Let $\mathbf{u}, \mathbf{v}$ , and $\mathbf{w}$ be vectors in $\mathbb{R}^n$ , and let $c$ be a scalar. Then
a. $\mathbf{u} \cdot \mathbf{v} = \mathbf{v} \cdot \mathbf{u} $
b. $(\mathbf{u} + \mathbf{v}) \cdot \mathbf{w} = \mathbf{u} \cdot \mathbf{w} + \mathbf{v} \cdot \mathbf{w}$
c. $(c\mathbf{u}) \cdot \mathbf{v} = c (\mathbf{u} \cdot \mathbf{v}) = \mathbf{u} \cdot (c\mathbf{v})$
d. $\mathbf{u} \cdot \mathbf{v} \ge 0 \; , \; \mbox{and} \; \mathbf{u} \cdot \mathbf{u} = 0 \; \mbox{if and only if} \; \mathbf{u} = \mathbf{0}$

동일한 공간에서 벡터와 스칼라 c 가 주어졌을 때, 위의 조건들을 만족한다.
d. 조건의 경우 동일한 벡터의 내적은 항상 0보다 크다. 각 항목의 제곱이기 때문이다. 또한 $\mathbf{u} \cdot \mathbf{u} = 0$ 이면 $\mathbf{u} = \mathbf{0}$ 이다.

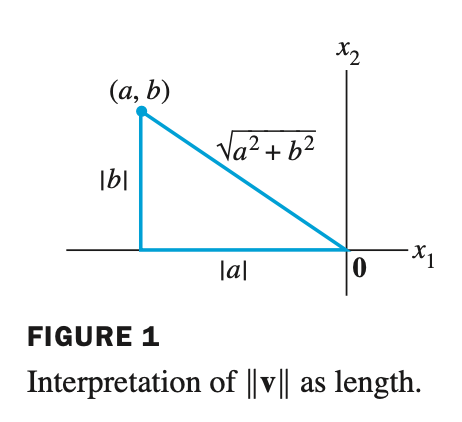
Length of a Vector - 벡터의 길이

The Length(or norm) of $\mathbf{v}$ is the nonnegative scalar $\lVert \mathbf{v} \rVert$ defined by
$\lVert \mathbf{v} \rVert = \sqrt{\mathbf{v} \cdot \mathbf{v}} = \sqrt{v_1^2 + v_2^2 + \dots + v_n^2} \; , \quad \mbox{and} \quad {\lVert \mathbf{v} \rVert}^2 = \mathbf{v} \cdot \mathbf{v}$

벡터의 길이는 동일한 벡터 두 개를 내적하고 루트를 씌운것과 같다. 동일한 벡터를 내적하게 되면 각 항목이 제곱이 되는데, 이는 피타고라스의 정리와 같다.

벡터의 길이 $\lVert \mathbf{v} \rVert$ 를 norm 이라고 한다.
norm 이 scalar 와 곱해졌을 때, 다음의 성질을 만족한다.

\[\lVert c\mathbf{v} \rVert = \lvert c \rvert \lVert \mathbf{v} \rVert\]

벡터의 길이가 1이면 이를 unit vector (유닛 벡터) 라고 한다.

\[\lVert \mathbf{u} \rVert = 1\]

또한 벡터 $\mathbf{v}$ 가 주어졌을 때, 각 항목을 norm 으로 나누면 길이가 유닛 벡터가 된다. 이처럼 벡터에 1/norm 을 곱해주는 것을 normalizing 이라고 한다.

\[\mathbf{u} = {1 \over {\lVert \mathbf{v} \rVert}} {\lVert \mathbf{v} \rVert}\]

normalizing 을 하게 되면 $\mathbf{v}$ 와 같은 방향을 가르키는 벡터가 되며 길이는 1이 된다.

예시 문제
벡터 $\mathbf{v}$ 가 주어졌을 때, $\mathbf{v}$ 와 같은 방향을 나타내며 길이가 1인 벡터 $\mathbf{u}$ 를 찾으시오.

\[\mathbf{v} = (1, -2, 2, 0)\] \[{\lVert \mathbf{v} \rVert}^2 = \mathbf{v} \cdot \mathbf{v} = (1)^2 + (-2)^2 + (2)^2 + (0)^2 = 9\] \[\lVert \mathbf{v} \rVert = \sqrt{9} = 3\]

\[\mathbf{u} = { 1 \over {\lVert \mathbf{v} \rVert}} \mathbf{v} = {1 \over 3} \mathbf{v} = {1 \over 3} \begin{bmatrix} \phantom{-}1 \\\ -2 \\\ \phantom{-}2 \\\ \phantom{-}0 \end{bmatrix} = \begin{bmatrix} 1 \over 3 \\\ -{2 \over 3} \\\ 2 \over 3 \\\ 0 \end{bmatrix}\]

$\mathbf{v}$ 의 norm 을 구하고, norm 을 $\mathbf{v}$ 에 나눠주면 찾을 수 있다.

Distance in $\mathbb{R}^n$ - $\mathbb{R}^n$ 공간에서의 거리

For $\mathbf{u}$ and $\mathbf{v}$ in $\mathbb{R}^n$ , the distance between $\mathbf{u}$ and $\mathbf{v}$ , wirtten as a $\; \mbox{dist} (\mathbf{u}, \mathbf{v})$ , is the length of the vector $\mathbf{u} - \mathbf{v}$ . That is
\[\mbox{dist} (\mathbf{u}, \mathbf{v}) = \lVert \mathbf{u} - \mathbf{v} \rVert\]

두 벡터의 차의 길이가 거리(distance)이다.

예시 문제 1
두 벡터가 다음과 같이 주어졌을 때, 두 벡터 사이의 거리를 구하라.

\[\mathbf{u} = (7, 1) \quad \mbox{and} \quad \mathbf{v} = (3, 2)\] \[\mathbf{u} - \mathbf{v} = \begin{bmatrix} 7 \\\ 1 \end{bmatrix} - \begin{bmatrix} 3 \\\ 2 \end{bmatrix} = \begin{bmatrix} \phantom{-}4 \\\ -1 \end{bmatrix}\] \[\lVert \mathbf{u} - \mathbf{v} \rVert = \sqrt{4^2 + (-1)^2} = \sqrt{17}\]

distance 를 일반화 해보면 다음과 같다.

\[\mathbf{u} = (u_1, u_2, u_3) \quad \mbox{and} \quad \mathbf{v} = (v_1, v_2, v_3)\] \[\mbox{dist}(\mathbf{u}, \mathbf{v}) = \lVert \mathbf{u} - \mathbf{v} \rVert = \sqrt{(\mathbf{u} - \mathbf{v}) \cdot (\mathbf{u} - \mathbf{v})} = \sqrt{(u_1 - v_1)^2 + (u_2 - v_2)^2 + (u_3 - v_3)^2 }\]

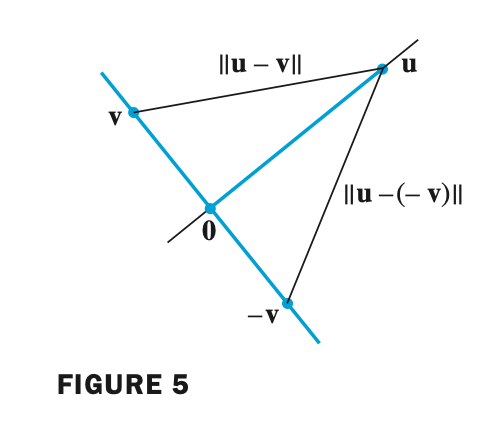
Orthogonal Vector - 직교 벡터

두 벡터가 Orthogonal(직교) 한다는 것은 perpendicular(수직)이라는 말과 같다. 즉 두 벡터 사이의 각도가 90도를 이루는 것을 바로 Orthogonal Vector(직교 벡터)라고 한다. 이 때 벡터는 임의의 모든 n차원에 해당된다.
다음은 두 벡터가 직교하려면 $\mbox{dist}(\mathbf{u}, \mathbf{v})$ 와 $\mbox{dist}(\mathbf{u}, -\mathbf{v})$ 가 같은지를 알아보자.

\[\mbox{dist}(\mathbf{u}, \mathbf{v}) = \lVert \mathbf{u} - \mathbf{v} \rVert = \sqrt{(\mathbf{u} - \mathbf{v}) \cdot (\mathbf{u} - \mathbf{v})} = \sqrt{\mathbf{u} \cdot \mathbf{u} - \mathbf{u} \cdot \mathbf{v} - \mathbf{v} \cdot \mathbf{u} + \mathbf{v} \cdot \mathbf{v}} = \sqrt{ {\lVert \mathbf{u} \rVert}^2 + {\lVert \mathbf{v} \rVert}^2 - 2\mathbf{u} \cdot \mathbf{v} }\] \[\mbox{dist}(\mathbf{u}, \mathbf{-v}) = \lVert \mathbf{u} - (-\mathbf{v}) \rVert = \sqrt{(\mathbf{u} + \mathbf{v}) \cdot (\mathbf{u} + \mathbf{v})} = \sqrt{\mathbf{u} \cdot \mathbf{u} + \mathbf{u} \cdot \mathbf{v} + \mathbf{v} \cdot \mathbf{u} + \mathbf{v} \cdot \mathbf{v}} = \sqrt{ {\lVert \mathbf{u} \rVert}^2 + {\lVert \mathbf{v} \rVert}^2 + 2\mathbf{u} \cdot \mathbf{v} }\]

여기서 두 거리가 동일하려면 다음과 같다

\[2\mathbf{u} \cdot \mathbf{v} = -2\mathbf{u} \cdot \mathbf{v}\]

이는 $\mathbf{u}$ 와 $\mathbf{v}$ 의 내적이 0이 되면 성립한다.

\[\mathbf{u} \cdot \mathbf{v} = 0\]

$\mbox{dist}(\mathbf{u}, \mathbf{v})$ 와 $\mbox{dist}(\mathbf{u}, -\mathbf{v})$ 가 동일하려면 $\mathbf{u} \cdot \mathbf{v} = 0$ 이 성립해야 하고, 직각인 경우에 두 거리가 동일하므로 결국
$\mathbf{u} \cdot \mathbf{v} = 0$ 이면 두 벡터가 직교(Orthogonal) 인 것을 의미한다.

Two vectors $\mathbf{u}$ and $\mathbf{v}$ in $\mathbb{R}^n$ are orthogonal (to each other) if $\mathbf{u} \cdot \mathbf{v} = 0 $ .

Theorem2. The Pythagorean Theorem
Two vectors $\mathbf{u}$ and $\mathbf{v}$ are orthogonal if and only if ${\lVert \mathbf{u} + \mathbf{v} \rVert}^2 = {\lVert \mathbf{u} \rVert}^2 + {\lVert \mathbf{v} \rVert}^2$ .

두 벡터가 직교하다면 $\mathbf{u} \cdot \mathbf{v} = 0$ 이므로 ${\lVert \mathbf{u} + \mathbf{v} \rVert}^2 = {\lVert \mathbf{u} \rVert}^2 + {\lVert \mathbf{v} \rVert}^2$ 피타고라스 정리를 만족한다.

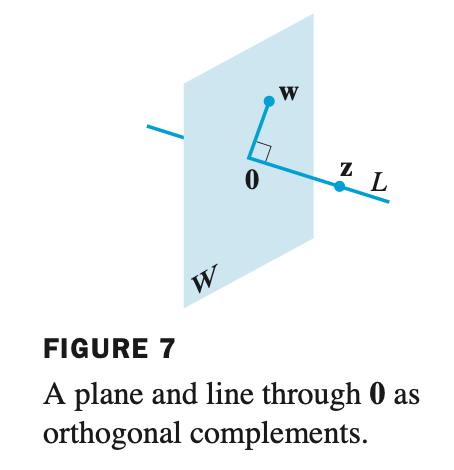
Orthogonal Complements - 직교 여공간

Let $W$ be a plane through the origin in $\mathbb{R}^3$
Let $L$ be the line throguh the origin and perpendicular to $W$
\[\mathbf{z} \cdot \mathbf{w} = 0\]
If a vector $\mathbf{z}$ is orthogonal to every vector in a subspace $W$ of $\mathbb{R}^n$
then, $\mathbf{z}$ is said to be orthogonal to $W$
The set of all vectors $\mathbf{z}$ that are orthogonal to $W$ is called the orthogonal complement of $W$ and denoted by $W^{\perp}$ .

$\mathbb{R}^3$ 공간에서 평면 $W$ 가 원점을 통과하고 원점을 통과하는 직선 $L$ 이 $W$ 와 직각이 되면 $L$ 에 있는 모든 벡터는 $\mathbf{w}$ 와 직교한다.
이는 $L$ 에 있는 임의의 벡터 $\mathbf{z}$ 와 평면 $W$ 의 임의의 벡터 $\mathbf{w}$ 의 내적은 0이 된다는 것을 뜻한다.
이처럼 $\mathbf{z}$ 가 $W$ 에 존재하는 모든 벡터와 직교하면 $\mathbf{z}$ 는 $W$ 에 직교한다고 말할 수 있다.
$\mathbf{z}$ 가 $W$ 에 직교하는 것을 $W$ 의 직교 여공간(Orthogonal Complements) 또는 수직(perpendicular) 라고 부르며 다음과 같이 표기한다.

\[W^{\perp}\]

위 그림(Figure 7) 에서 $W$ 와 $L$ 은 직교하므로 다음과 같이 표기할 수 있다.

\[L = W^{\perp} \quad \mbox{and} \quad W = L^{\perp}\]

추가적으로 0 벡터는 모든 벡터와의 내적이 0이므로 모든 벡터에 직교한다.

예시 문제

Example 1
Suppose a vector $\mathbf{y}$ is orthogonal to vectors $\mathbf{u}$ and $\mathbf{v}$ .
Show that $\mathbf{y}$ is orthogonal to the vector $\mathbf{u} + \mathbf{v}$ .

두 벡터가 직교하다는 것은 $\mathbf{u} \cdot \mathbf{v} = 0$ 이므로 다음과 같이 접근할 수 있다.

\[\mathbf{y} \cdot \mathbf{u} = 0\] \[\mathbf{y} \cdot \mathbf{v} = 0\] \[\mathbf{y} \cdot (\mathbf{v} + \mathbf{u}) = \mathbf{y} \cdot \mathbf{v} + \mathbf{y} \cdot \mathbf{u} = 0\]

따라서 벡터 $\mathbf{y}$ 는 $\mathbf{v} + \mathbf{u}$ 에 직교한다.

Example 2
Suppose a vector $\mathbf{y}$ is orthogonal to vectors $\mathbf{u}$ and $\mathbf{v}$ .
Show that $\mathbf{y}$ is orthogonal to every $\mathbf{w}$ in Span{$\mathbf{u},\mathbf{v}$}.

Span{$\mathbf{u},\mathbf{v}$} 는 다음과 같이 linear combination 형태로 나타낼 수 있다.

\[\mathbf{w} = c_1\mathbf{u} + c_2\mathbf{v}\]

여기에 $\mathbf{y}$ 벡터를 내적해주면

\[\mathbf{w} \cdot \mathbf{y} = (c_1\mathbf{u} + c_2\mathbf{v}) \cdot \mathbf{y} = c_1\mathbf{u} \cdot \mathbf{y} + c_2\mathbf{v} \cdot \mathbf{y} = 0\]

따라서 벡터 $\mathbf{y}$ 는 모든 Span{$\mathbf{u},\mathbf{v}$} 에 직교한다.

Example 3
Let $W = \mbox{Span}$ { $v_1 , \dots, v_p$ }. Show that if $\mathbf{x}$ is orthogonal to each $\mathbf{v}_j$ , then $\mathbf{x}$ is orthogonal to every vector in $\mathbf{W}$ .

벡터 $\mathbf{x}$ 가 임의의 벡터 $\mathbf{v}_j$ 에 직교하므로 다음과 같이 나타낼 수 있다.

\[\mathbf{x} \cdot \mathbf{v}_j = 0 , \quad \mbox{for} \; 1 \le j \le p\]

subspace $\mathbf{w}$ 를 다음과 같이 linear combination 형태로 표현할 수 있다.

\[\mathbf{w} = c_1\mathbf{v}_1 + \dots + c_p\mathbf{v}_p\]

$\mathbf{x}$ 를 inner product 를 취해주면 다음과 같다.

\[\mathbf{w} \cdot \mathbf{x} = c_1\mathbf{v}_1 \cdot \mathbf{x} + \dots + c_p\mathbf{v}_p \cdot \mathbf{x} = 0\]

임의의 subspace $\mathbf{w}$ 와 벡터 $\mathbf{x}$ 는 orthogonal 하다.

Example 4
Let $W$ be a subspace of $\mathbb{R}^n$ , and let $W^{\perp}$ be the set of all vectors orthogonal to $W$ .
Show that $W^{\perp}$ is a subspace of $\mathbb{R}^n$ .

$W$ 가 $\mathbb{R}^n$ 의 subspace 이면 $W^{\perp}$ 도 $\mathbb{R}^n$ subspace 인지 증명해보자.
우선, 복습차원에서 subspace 를 만족하는 3가지 조건을 살펴보자

zero vector 가 subspace 에 포함되어야 한다.
vector sum 과
scalar multiplication 가 같은 공간에 존재해야한다.

다음과 같이 가정해보자

\[\mathbf{u} \; \mbox{in} \; W \quad \quad \mathbf{z} \; \mbox{in} \; W^{\perp}\]

scalar multiplication 이 orthogonal 한지 살펴보자

\[\mathbf{u} \cdot c\mathbf{z} = c\mathbf{u} \cdot \mathbf{z} = 0\]

따라서 $c\mathbf{z} \; \mbox{in} \; W^{\perp} $ 를 만족한다.

$\mathbf{z}_1 \; \mbox{and} \; \mathbf{z}_2 \; \mbox{in} \; W^{\perp} $ 일 때 orthogonal 한지 살펴보자

\[\mathbf{u} \cdot (\mathbf{z}_1 + \mathbf{z}_2) = \mathbf{u} \cdot \mathbf{z}_1 + \mathbf{u} \cdot \mathbf{z}_2 = 0\]

따라서 $\mathbf{z}_1 + \mathbf{z}_2$ 역시 in $W^{\perp}$ 임을 만족한다.

마지막으로 0 벡터는 모든 벡터에 orthogonal 하므로 $\mathbf{0} \; \mbox{in} \; W^{\perp}$ 임을 만족하므로
세 가지 조건 모두를 충족하므로 W가 subspace 이면 W perpendicular 또한 subspace 이다.

Theorem3.
Let $A$ be an $m \times n$ matrix. The orthogonal complement of the row space of $A$ is the null space of $A$ , and the orthogonal complement of the column space of $A$ is the null space of $A^T$ :
\[(\mbox{Row} \; A)^{\perp} = \mbox{Nul} \; A \quad \quad \mbox{and} \quad \quad (\mbox{Col} \; A)^{\perp} = \mbox{Nul} \; A^T\]

null space 이기 위해서는 다음과 같다. $ A\mathbf{x} = 0 $ 이며 $\mathbf{x} \; \mbox{in} \; \mathbb{R}^n $ 이다.

\[A\mathbf{x} = \begin{bmatrix} \mbox{row}_1(A) \\\ \mbox{row}_2(A) \\\ \vdots \\\ \mbox{row}_m(A) \end{bmatrix} \mathbf{x} = \begin{bmatrix} \mbox{row}_1(A)\mathbf{x} \\\ \mbox{row}_2(A)\mathbf{x} \\\ \vdots \\\ \mbox{row}_m(A)\mathbf{x} \end{bmatrix} = 0\] \[\mbox{row}_i(A) = [a_{i1} \quad a_{i2} \quad \dots \quad a_{in}]\] \[\mathbf{u}_i = (\mbox{row}_i(A))^T = \begin{bmatrix} a_{i1} \\\ a_{i2} \\\ \vdots \\\ a_{in} \end{bmatrix}\]

위 식은 i-th columns of $A^T$ 임을 의미한다.

\[\mathbf{u}_i \cdot \mathbf{x} = \mathbf{u}_i^T \mathbf{x} = 0 \; , \quad \mbox{for} \; 1 \le i \le m\]

Nul $A$ 는 $A\mathbf{x} = 0$을 만족하는 모든 $\mathbf{x}$ 집합을 의미한다.
Row $A$ 는 $A$ 의 모든 row를 벡터로 만들어서 span 한 행 공간(row space) 를 의미한다.
Col $A$ 는 $A$ 의 모든 column을 벡터로 만들어서 span 한 열 공간(column space) 를 의미한다.
Row $A$ 의 perpendicular는 $A$ 의 null space 이다.
Col $A$ 의 perpendicular 는 $A^T$ 의 null space 이다.