---

The matrix of Linear Transformation - 선형 변환의 행렬

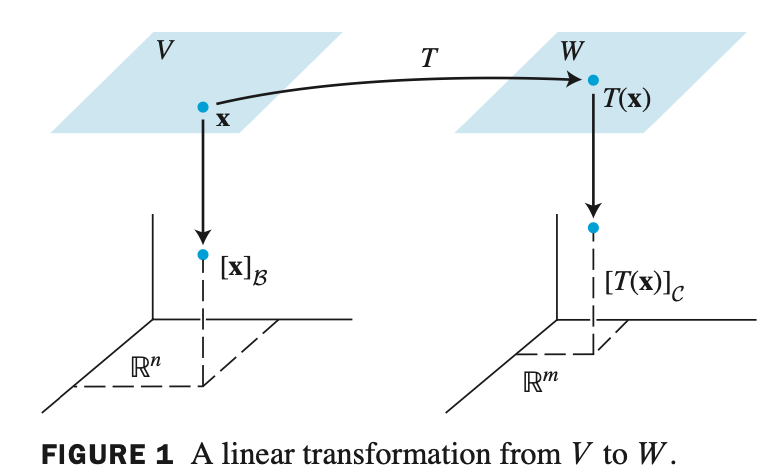
• $V$ 가 n-dimensional vector space 이고 $W$ 는 m-dimensional vector space 로 주어졌을 때, $V$ 에서 $W$ 로 linear transformation 을 $T$ 로 가정하자.

• 그러면 $\beta$ basis 로 표현되는 $\mathbf{x}$ 의 coordinate vector \(\left[ \mathbf{x} \right] _{\beta}\) 와 $\mathcal{C}$ basis 로 표현되는 $T(\mathbf{x})$ 의 coordinate vector $[T(\mathbf{x})]_{\mathcal{C}}$ 를 연결시키는 행렬이 있을까?

• \(\left[ \mathbf{x} \right] _{\beta}\) 와 $[T(\mathbf{x})]_{\mathcal{C}}$ 사이의 연결은 쉽게 찾을 수 있다.
• $V$ 에 대한 basis $\beta$ 가 ${\mathbf{b}_1, \dots, \mathbf{b}_n}$ 으로 구성되어 있다면
• $\mathbf{x}$ 는 다음과 같이 정의할 수 있다.

\[\mathbf{x} = r_1\mathbf{b}_1 + \dots + r_n\mathbf{b}_n\]

• 따라서 basis $\beta$ 에 대한 coordinate vector \(\left[ \mathbf{x} \right] _{\beta}\) 는 다음과 같다.

\[\left[ \mathbf{x} \right] _{\beta} = \begin{bmatrix} r_1 \\\ \vdots \\\ r_n \end{bmatrix}\]

• 그리고 $T(\mathbf{x})$ 는 다음과 같이 정의된다.

\[T(\mathbf{x}) = T(r_1\mathbf{b}_1 + \dots + r_n\mathbf{b}_n) = r_1T(\mathbf{b}_1) + \dots + r_nT(\mathbf{b}_n)\]

• basis $\mathcal{C}$ 에 대한 $T(x)$ 의 coordinate vector 는 다음과 같이 구할 수 있다.

\[[T(\mathbf{x})]_{\mathcal{C}} = r_1[T(\mathbf{b}_1)]_{\mathcal{C}} + \dots + r_n[T(\mathbf{b}_n)]_{\mathcal{C}}\]

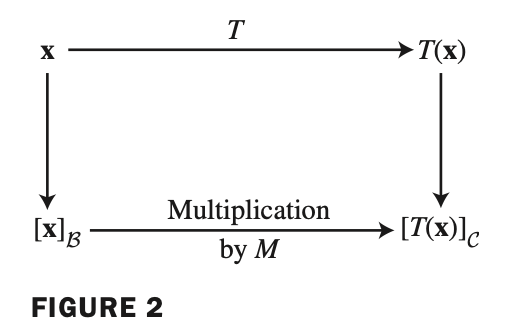
• 이를 행렬 $M$ 을 이용해 간단히 표현하면 다음과 같다.

\[[T(\mathbf{x})]_{\mathcal{C}} = M \left[ \mathbf{x} \right] _{\beta}\]

• 여기서 $M$ 은 다음과 같다.

\[M = [ [T(\mathbf{b}_1)]_{\mathcal{C}} \quad \dots \quad [T(\mathbf{b}_n)]_{\mathcal{C}} ]\]

이 행렬 $M$ 을 bases 인 $\beta$ 와 $\mathcal{C}$ 에 상대적인 $T$ 에 대한 행렬 이라고 부른다.
The matrix $M$ is a matrix representation of $T$, called the matrix for $T$ relative to the bases $\beta$ and $\mathcal{C}$ .

• 예시 문제
• vector space $V, W$ 에 대한 basis $\beta, \mathcal{C}$ 와 $T(b)$ 주어졌을 때, basis $\beta$ 와 $\mathcal{C}$ 에 상대적인 $T$ 에 대한 행렬 $M$ 을 찾는 문제이다.

\[\beta = {\mathbf{b}_1, \mathbf{b}_2}\] \[\mathcal{C} = {\mathbf{c}_1, \mathbf{c}_2, \mathbf{c}_3 }\] \[T(\mathbf{b}_1) = 3\mathbf{c}_1 - 2\mathbf{c}_2 + 5\mathbf{c}_3 \quad \mbox{and} \quad T(\mathbf{b}_2) = 4\mathbf{c}_1 + 7\mathbf{c}_2 - \mathbf{c}_3\]

• $ M = [T(\mathbf{b})]_{\mathcal{C}} $ 이므로 다음과 같이 구할 수 있다.

\[[T(\mathbf{b}_1)]_{\mathcal{C}} = \begin{bmatrix} \phantom{-}3 \\\ -2 \\\ \phantom{-}5 \end{bmatrix} \quad \mbox{and} \quad [T(\mathbf{b}_2)]_{\mathcal{C}} = \begin{bmatrix} \phantom{-}4 \\\ \phantom{-}7 \\\ -1 \end{bmatrix}\]

• 두 벡터의 column 으로 구성된 행렬 $M$ 을 구할 수 있다.

\[M = \begin{bmatrix} \phantom{-}3 & \phantom{-}4 \\\ -2 & \phantom{-}7 \\\ \phantom{-}5 & -1 \end{bmatrix}\]

Linear Transformations from V into V - 동일한 벡터 공간에서의 선형 변환

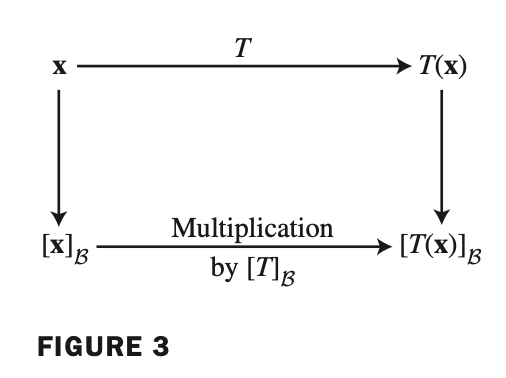
• 동일한 벡터 공간에서 선형 변환은 다음과 같이 정의된다.

\[[T(\mathbf{x})]_{\beta} = [T]_{\beta} [\mathbf{x}]_{\beta}\]

• 이를 $\beta$ - matrix for $T$ 라고 간단히 표현한다.

• 예시 문제
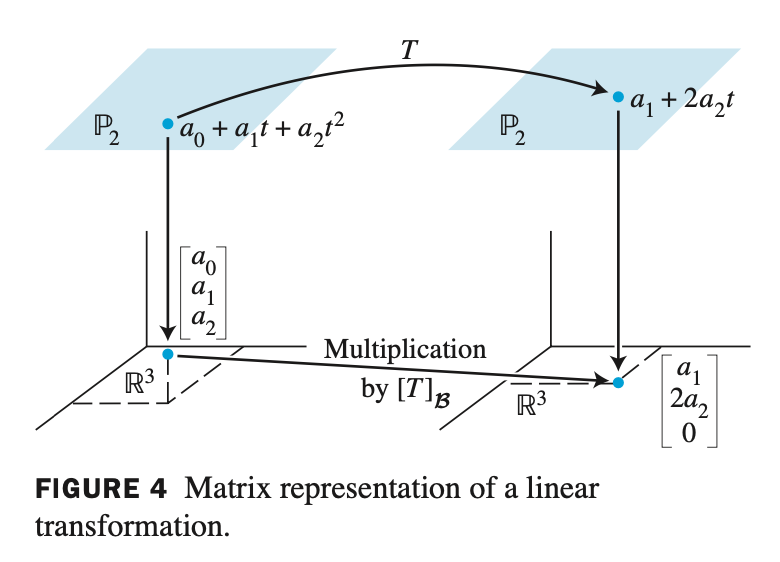
• $T$ 가 $P_2 \rightarrow P_2$ 로 mapping 한다고 정의되고 $T(\mathbf{x})$ 는 다음과 같다. (여기서 $P$ 는 polynomial space 를 의미한다.)

\[T(a_0 + a_1t + a_2t^2) = a_1 + 2a_2t\]

• (1) $\beta$ basis 가 ${1, t, t^2}$ 일 때, B-matrix for $T$ 를 찾고 (2) \([T(\mathbf{p})]_{\beta} = [T]_{\beta} [\mathbf{p}]_{\beta}\) 를 증명하는 문제이다.

(1)

• basis vector 를 구하면 다음과 같다.

$ T(1) = 0 \quad \quad $ The zero polynomial

$ T(t) = 1 \quad \quad $ The polynomial whose value is always 1.

$ T(t^2) = 2t \quad \quad $

• $R^3$ space 의 basis 인 ${1, t, t^2}$ 에 대한 coordinate vector 는 다음과 같다.

\[[T(\mathbf{1})]_{\beta} = \begin{bmatrix} 0 \\\ 0 \\\ 0 \end{bmatrix} \; , \quad [T(\mathbf{t})]_{\beta} = \begin{bmatrix} 1 \\\ 0 \\\ 0 \end{bmatrix} \; , \quad [T(\mathbf{t^2})]_{\beta} = \begin{bmatrix} 0 \\\ 2 \\\ 0 \end{bmatrix}\] \[[T]_{\beta} = \begin{bmatrix} 0 & 1 & 0 \\\ 0 & 0 & 2 \\\ 0 & 0 & 0 \end{bmatrix}\]

(2)

• $ [T(\mathbf{p})]_{\beta} $ 는 다음과 같다.

\[[T(\mathbf{p})]_{\beta} = [a_1 + 2a_2t]_{\beta} = \begin{bmatrix} a_1 \\\ 2a_2 \\\ 0 \end{bmatrix} = \begin{bmatrix} 0 & 1 & 0 \\\ 0 & 0 & 2 \\\ 0 & 0 & 0 \end{bmatrix} \begin{bmatrix} a_0 \\\ a_1 \\\ a_2 \end{bmatrix} = [T]_{\beta} [\mathbf{p}]_{\beta}\]

• 결과적으로 우리가 $T$ 를 알고 $[T]_{\beta}$ ($T$ 에 대한 $\beta$ 행렬) 을 알면 coordinate vector 를 알 수 있고 따라서 해당 Transformation 에 대응되는 polynomial 을 찾을 수 있다.

Theorem7. Diagonal Matrix Representation

Suppose $A = PDP^{-1} \; $ , where $D$ is a diagonal $n \times n$ matrix. If $\beta$ is the basis for $\mathbb{R}^n$ formed from the columns of $P$ , then $D$ is the $\beta$ - matrix for the transformation $\mathbf{x} \mapsto A\mathbf{x}$ .

• $D$ 는 diagonal matrix 이고, $A$ 는 diagonalizable 로 가정할 때 basis $\beta$ 는 $P$ 의 column 으로 구성된다. 그리고 $D$ 는 $\beta$ - matrix for $T$ 가 된다.

• 증명
• $P$ 의 column 은 $\mathbf{b}_1 , \dots , \mathbf{b}_n \; $ 이므로 $\beta = {\mathbf{b}_1 , \dots , \mathbf{b}_n} $ 이다.
• 따라서 $P$ 는 change-of-coordinates matrix $P_{\beta}$ 이다. 그러모르 다음과 같은 성질을 만족한다.

\[P[\mathbf{x}]_{\beta} = \mathbf{x} \quad \mbox{and} \quad [\mathbf{x}]_{\beta} = P^{-1}\mathbf{x}\]

• 만약, $T(\mathbf{x}) = A\mathbf{x}$ 이면 다음과 같다.

\([T]_{\beta} = [ [T(\mathbf{b}_1)]_{\beta} \quad \dots \quad [T(\mathbf{b}_n)]_{\beta} ] \quad \quad \quad \quad\) Definition of $[T]_{\beta}$

\(\quad \quad = [ [A\mathbf{b}_1]_{\beta} \quad \dots \quad [A\mathbf{b}_n]_{\beta} ] \quad \quad \quad \quad\) Since $T(\mathbf{x}) = A\mathbf{x}$

\(\quad \quad = [ P^{-1}A\mathbf{b}_1 \quad \dots \quad P^{-1}A\mathbf{b}_n ] \quad \quad \quad \quad\) Change of coordinates

\(\quad \quad = P^{-1}A [\mathbf{b}_1 \quad \dots \quad \mathbf{b}_n ] \quad \quad \quad \quad\) Matrix multiplication

$ \quad \quad = P^{-1}AP $

• $A = PDP^{-1} $ 이므로 $[T]_{\beta}$ 는 다음과 같다.

\[[T]_{\beta} = P^{-1}AP = D\]

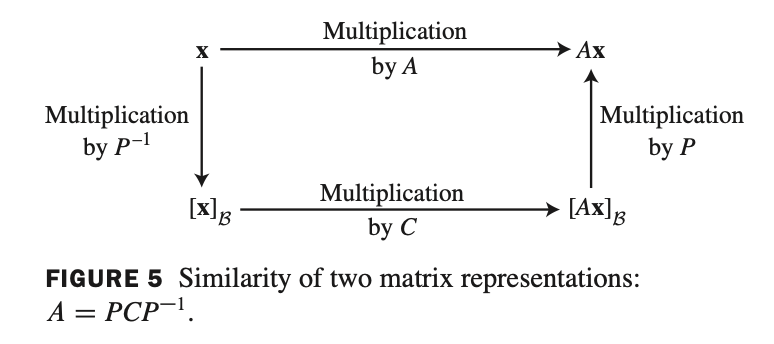
Similarity of Matrix Representations - 행렬의 유사도 표현

• $A$ 와 $C$ 가 similar 하면, $\beta$ - matrix 는 $C$ 이다.
• $C$ 가 꼭 diagonal matrix 가 아니어도 성립한다..

\[A = PCP^{-1}\]

• 예시 문제

\[A = \begin{bmatrix} \phantom{-}4 & -9 \\\ \phantom{-}4 & -8 \end{bmatrix} \; , \; \mathbf{b}_1 = \begin{bmatrix} 3 \\\ 2 \end{bmatrix} \; , \; \mathbf{b}_2 = \begin{bmatrix} 2 \\\ 1 \end{bmatrix}\]

• $A$ 와 basis 가 주어지고 $\beta$ - matrix 를 찾는 문제이다.

• 여기서 $A$ 의 eigenvalue 는 -2 (multiplicity = 2) 이고 eigenspace dimension 은 1이다. 따라서, not diagonalizable 이다.

• $\mathbf{b}_1 , \mathbf{b}_2$ 는 서로 곱의 관계가 아니므로 linearly independent 함을 알 수 있다.
• 따라서 $P$ 를 구할 수 있다.

\[AP = \begin{bmatrix} \phantom{-}4 & -9 \\\ \phantom{-}4 & -8 \end{bmatrix} \begin{bmatrix} 3 & 2 \\\ 2 & 1 \end{bmatrix} = \begin{bmatrix} -6 & -1 \\\ -4 & \phantom{-}0 \end{bmatrix}\]

• $A = PCP^{-1}$ 이므로 $C$ 는 다음과 같이 구할 수 있다.

\[P^{-1}AP = \begin{bmatrix} -1 & \phantom{-}2 \\\ \phantom{-}2 & -3 \end{bmatrix} \begin{bmatrix} -6 & -1 \\\ -4 & \phantom{-}0 \end{bmatrix} = \begin{bmatrix} -2 & \phantom{-}1 \\\ \phantom{-}0 & -2 \end{bmatrix}\]

• $C$ 의 diagonal entries 가 $A$ 의 eigenvalue 가 되고 $\beta$ - matrix 이다.
• $A$ 가 diagonalizable 이 아니더라도 어떤 independent basis 만 선택한다면 $\beta$ - matrix 를 찾을 수 있다. 이때 basis 는 independent set 이어야 한다.