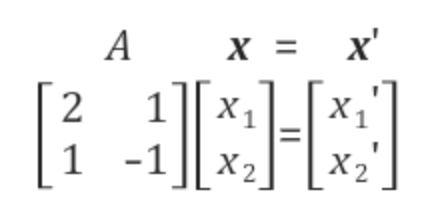Linear Algebra - 4.1 Eigenvectors and Eigenvalues
용어 정리
- eigenvalue - 고유값
- eigenvector - 고유벡터
- eigenspace - 고유공간
Eigenvalue 와 Eigenvector 의 기본 아이디어
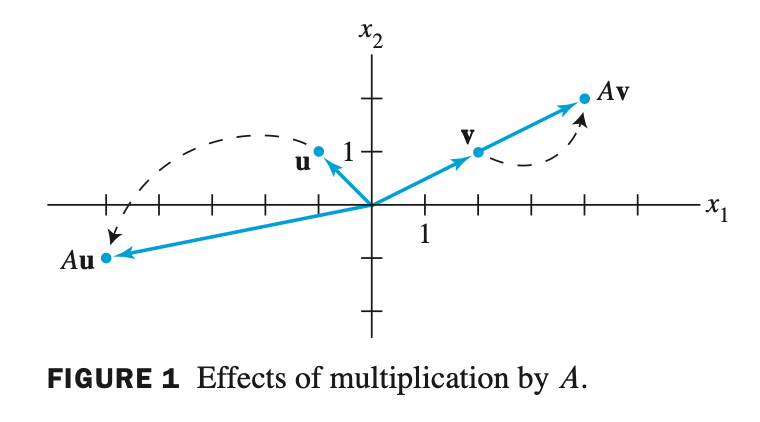
- $ A = \begin{bmatrix} 3 & -2 \\ 1 & 0 \end{bmatrix} \quad , \quad \mathbf{u} = \begin{bmatrix} -1 \\ \phantom{-}1 \end{bmatrix} \quad , \mbox{and} \; \mathbf{v} = \begin{bmatrix} 2 \\ 1 \end{bmatrix}$
- $ A\mathbf{u} = \begin{bmatrix} -5 \\ -1 \end{bmatrix} \quad \quad A\mathbf{v} = \begin{bmatrix} 4 \\ 2 \end{bmatrix} = 2\mathbf{v} $
- $A\mathbf{v}$ 의 결과는 동일한 직선상에 solution 이 존재한다. 이것이 eigenvalue 와 eigenvector 의 기본 idea 이다.
Eigenvector - 고유 벡터
An eigenvector of an $n \times n$ matrix $A$ is a nonzero vector $\mathbf{v}$ such that $A\mathbf{x} = \lambda\mathbf{x}$ for some scalar $\lambda$ . A scalar $\lambda$ is called an eigenvalue of $A$ if there is nontrivial solution $\mathbf{x}$ of $A\mathbf{x} = \lambda\mathbf{x}$ ; such an $\mathbf{x}$ is called an eigenvector corresponding to $\lambda$ .
- $A\mathbf{x} = \lambda\mathbf{x}$ 를 만족하는 nonzero vector x 가 eigenvector 이다.
- 또한, $A\mathbf{x} = \lambda\mathbf{x}$ 에서 x가 nontrivial solution 이 존재할 때 scalar $\lambda$ 가 eigenvalue 가 된다.
- 여기서 x 를 $\lambda$ 에 상응하는 eigenvector 라고 한다.
- 예시 문제 1
- u와 v가 A의 eigenvector 인가?
- $A\mathbf{x} = \lambda\mathbf{x}$ 만족하는지를 확인하면 된다.
- u는 A의 eigenvector, -4는 A의 eigenvalue 가 된다.
- v는 A의 eigenvector 가 아니다.
- 예시 문제 2
- 7 이 A의 eigenvalue 인지 파악하고 그에 해당하는 eigenvector 를 찾아라.
- 위의 식을 다음과 같이 homogeneous equation 으로 나타낼 수 있다.
- 여기서 x 는 nonzero vector 가 되어야 하며, 이 homogeneous equation 이 nontrivial solution 인지 파악하면 된다.
- nontrivial solution 을 파악하기 위해 zero vector 를 포함한 augmented matrix를 row reduction 후 free variable 이 존재하는지 파악하면 된다.
- $x_2$ 가 free variable 이다.
- $x_2$ 를 다음과 같이 general solution 으로 나타낼 수 있다.
- 따라서, $x_2 \ne 0$ 이고 nontrivial solution 이 존재하므로 7은 A의 eigenvalue 임을 성립한다.
- 여기서 [1,1] 은 eigenspace 이다.
Eigenspace - 고유 공간
$\lambda$ is an eigenvalue of $A$ if and only if the equation $(A - \lambda I) = 0$ has a nontrivial solution. It means the set of all solutions are the null space of the matrix $A - \lambda I$ . So this set is a subspace of $\mathbb{R}^n$ and is called the eigenspace of $A$ corresponding to $\lambda$ . The eigenspace consists of the zero vector and all the eigenvectors corresponding to $\lambda$ .
- $\lambda$ 가 A의 eigenvalue 이면, $(A - \lambda I) = 0$ 는 nontrivial solution 을 갖는다.
- $\lambda$ 에 해당하는 A의 eigenspace는 $A - \lambda I$ 행렬의 null space 이다.
- eigenspace 는 zero vector 와 $\lambda$ 에 해당하는 eigenvectors 두 가지를 포함한다. zero vector 는 eigenvector 에 포함되지 않지만, eigenspace 에는 포함된다.
- 예시 문제
- $\lambda = 2$ 에 해당하는 eigenspace 를 찾고 basis를 찾아라.
- homogeneous equation 에서 nontrivial solution 이 존재하는지 판단하기 위해 augmented matrix를 만들고 row reduction 을 통해 free variable 이 존재하는지 확인하자.
- $x_2, x_3$ 가 free variable 이다.
- general solution 으로 표현 해보면 다음과 같다.
- 두 개의 vector 는 independent vector 이며 eigenvector 이다.
- 두 vector 가 independent set 이므로 basis는 다음과 같다.
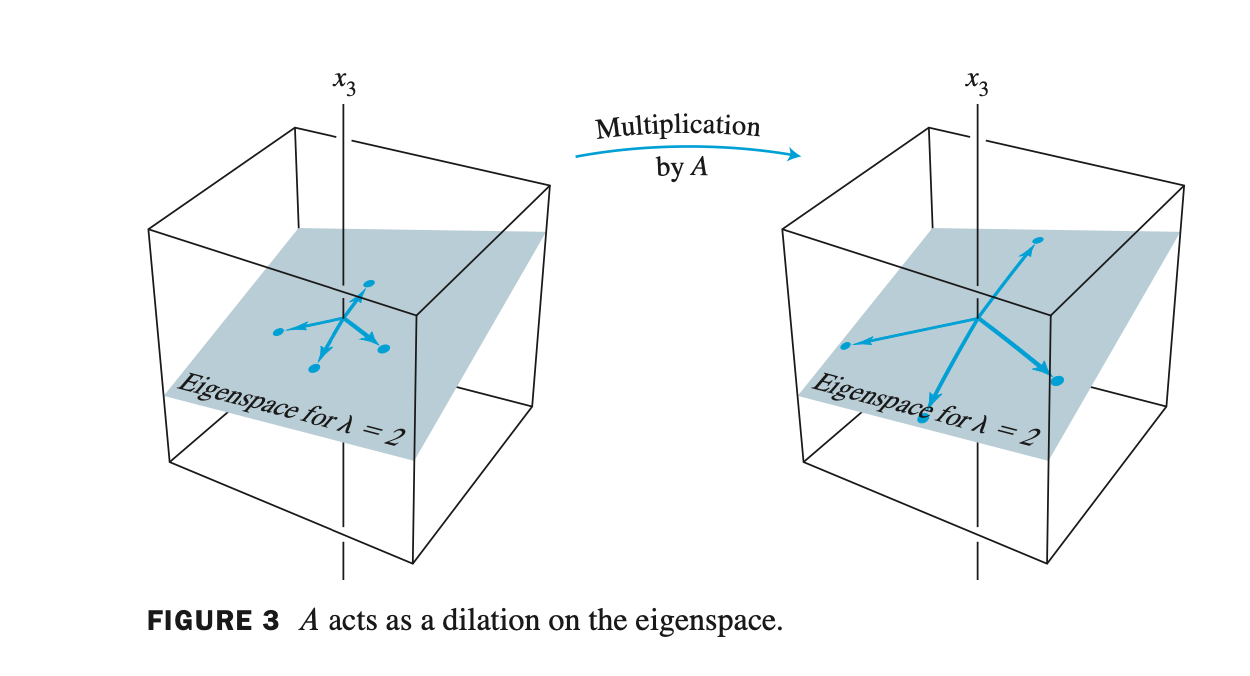
- 3차원 space에 $\lambda = 2$ 에 대한 eigenspace 가 주어졌다고 가정하자.
- eigenspace 는 zero vector 와 eigenvector 들을 포함한다.
- eigenspace 에 존재하는 임의의 vector 4 개를 선택하여 행렬 A 곱을 하면 크기가 2배씩 늘어나게 된다.
Theorem1.
The eigenvalues of a triangular matrix are the entries on its main diagonal.
triangular matrix 의 eigenvalue 는 diagonal term 들 이다.
- 증명
- (1) A가 upper triangular matrix 인 경우
- 위 방정식에서 nontrivial solution 이 존재해야한다 이는 free variable 이 존재한다는 뜻이므로 pivot position 이 0이 되어야 한다.
- 따라서 eigenvalue 인 $\lambda$ 는 {a_{11}, a_{22}, a_{33}} 가 될 수 있다.
- $\lambda$ 의 개수는 $n \times n$ 행렬 기준으로 항상 n 개 이하가 되어야 하므로, 위 예시에서는 3개 이하이다.
- (2) A 가 lower triangular matrix 인 경우
- $A$ 와 $A^T$ 가 동일한 eigen value 를 갖고 있다는 것을 증명하면 된다.
- $\lambda I$ 가 diagonal term 만 존재하므로 다음의 식이 성립한다. (항등행렬이란 뜻)
- $A - \lambda I$ 는 free variable 이 존재하고, lower triangular matrix 이므로 $\mbox{det} = 0$ 이 되어 not invertible 이 된다.
- 역행렬의 성질에 의해 $(A- \lambda I)^T$ 도 not invertible 이 된다.
- 따라서 $(A^T - \lambda I)$ 역시 not invertible 이 된다.
- A 행렬을 trnaspose 하여도 diagonal term 은 변하지 않으므로 $A$ 와 $A^T$ 는 동일한 eigenvalue 를 갖게 된다.
eigenvalue 가 0 인 경우
The scalar $\lambda$ is an eigenvalue of $A$ if and only if the equation $(A - \lambda I)\mathbf{x} = \mathbf{0}$ has a nontrivial solution, that is, if and only if the equation has a free variable, that is, if and only if $A$ is not invertible.
- $A$ 의 eigenvalue 가 0이면 $A$ 는 not invertible 이다.
- eigenvector 는 nonzero vector 이어야 한다.
- eigenvalue 는 0이어도 된다.
- $A\mathbf{x} = \lambda$ 에서 $\lambda = 0$ 이면 $A\mathbf{x} = 0$ 인 homogeneous equation 이 된다.
- 이 homogeneous equation 이 nontrivial solution 이 존재한다면 eigenvector 가 존재한다.
- 따라서 $\lambda = 0$ 인 경우에도 eigenvector는 존재하게 된다.
Theorem2.
If $\mathbf{v_1} , \dots , \mathbf{v_r}$ are eigenvectors that correspond to distinct eigenvalues $\lambda _{1} , \dots , \lambda _{r}$ of an $n \times n$ matrix $A$ , then the set { $ v_1 , \dots , v_r$ } is linearly independent.
$n \times n$ 행렬 $A$ 의 별개의 eigenvalue에 해당하는 eigenvector 는 linearly independent set 이다.
- 증명
- {$v_1 , \dots , v_r$} 이 linearly dependent 이고, $v_1$ 이 nonzero 라고 가정해보자. linearly dependent set 의 성질에 의해 v_{p + 1} 은 다음과 같이 표현 가능하다.
- 여기서 A를 곱하면 다음과 같다.
- $A\mathbf{v} = \lambda \mathbf{v}$ 이므로 아래와 같이 표현이 가능하다.
- 위 두식을 빼면 다음과 같다
- $\lambda$ 는 distinct 이므로 $ \lambda _1 - \lambda _{p+1}$ 은 nonzero 가 된다.
- 따라서 coefficient인 $c_1 , \dots, c_p$ 가 무조건 0이 되어야 한다.
이는 trivial solution 만 존재한다는 의미이며 linearly dependent 로 가정했던 것에 모순이 된다.
- 즉, distinct eigenvalue 가 주어지고 그에 해당하는 eigenvector set 은 무조건 linearly independent set 이 된다.
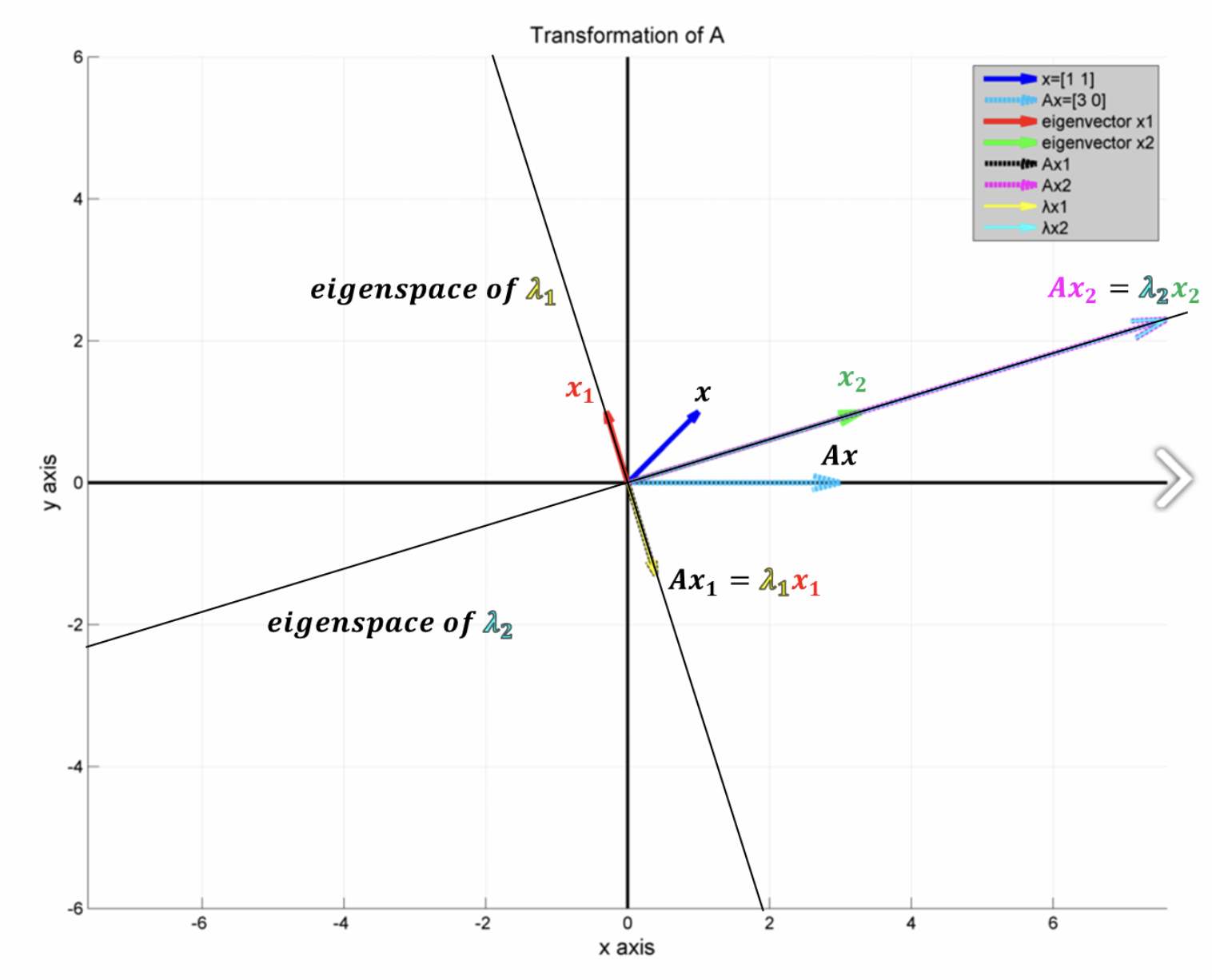
기하학적으로 eigenvalue, eigenvector, eigenspace 를 확인해보자.
- 우선 다음과 같은 $2 \times 2$ 크기의 linear system equation A 를 살펴보자.
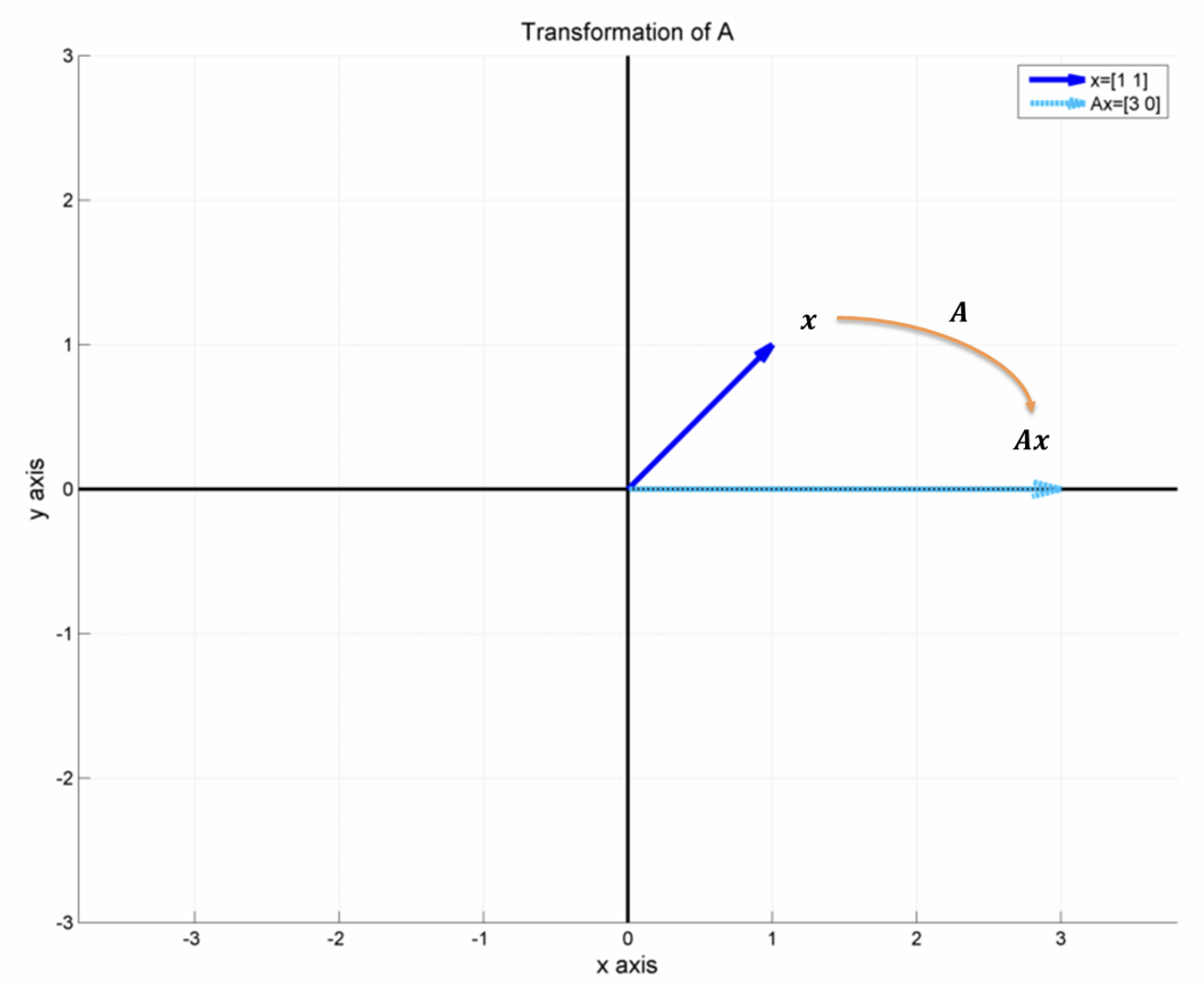
- 다음 그래프는 A 에 x = [1 1] 를 곱한 linear transformation 을 나타낸 것이다.
- x = [1 1] 이외에도 다른 수많은 벡터들을 A에 곱하여 linear transformation 을 하여도 원래 벡터방향과는 다른 쪽으로 변환이 이루어진다.
- 하지만, 우리가 eigenvector 의 정의를 살펴봤듯이, 그 수많은 벡터들 중 어떤 벡터들은 A에 곱하여도 그 방향이 변하지 않거나 원래 자기 자신과 평행한 벡터들이 있다는것을 확인했다.
- 이러한 벡터들이 바로 그 행렬 A의 eigenvector 이다. 다음 그래프는 행렬 A에 대한 eigenvector 를 나타낸 것이다.
- 일반적으로 $n \times n$ 행렬은 n 개의 eigenvector 를 갖는다.
- 다음은 우리가 $A\mathbf{x} = \lambda \mathbf{x}$ 임을 나타내는 기하학적 그래프이다.
- 즉 행렬 A 에 의해 변환된 eigenvector x 는 원래의 벡터에 어떤 상수, eigenvalue 인 $\lambda$ 를 곱한것과 같다.
- 결론은 eigenvalue 는 유일하며, eigenvector 는 무수히 많다.
- 또한 우리는 eigenspace 를 배웠다. eigenspace 란 eigenvector 들이 형성하는 subspace 라고 보면 된다.
- 즉, 행렬 A의 eigenvector 들은 eigenspace 상에 존재하는 무수히 많은 벡터들이다.
- 또한 여기서 eigenvalue 가 0 인 경우 Ax = 0 이 되는것을 위에서 살펴보았다.
- 즉, 이때의 eigenvector 는 null space 에 존재하는것이다. 다시 말하면 행렬 A 가 singular matrix 라는 것.