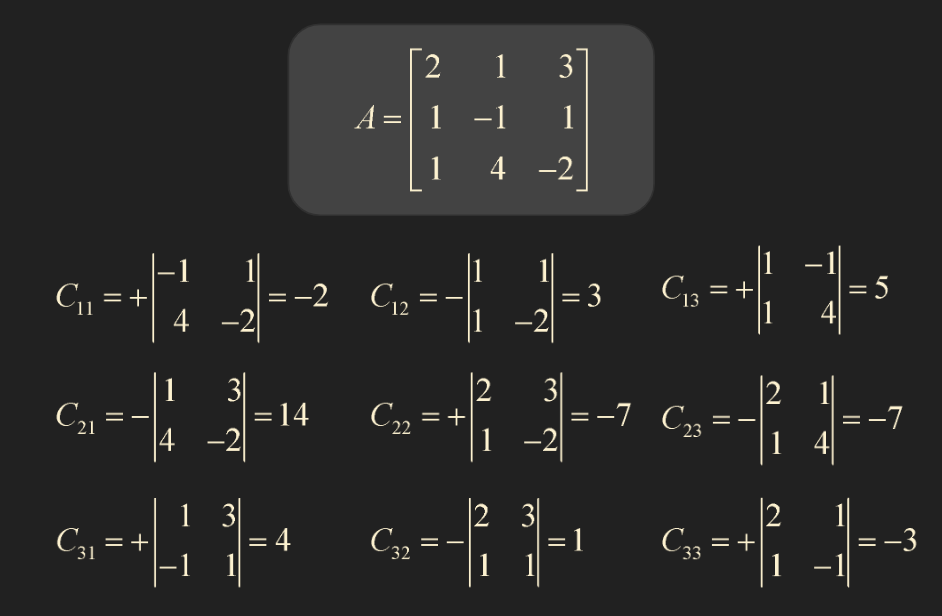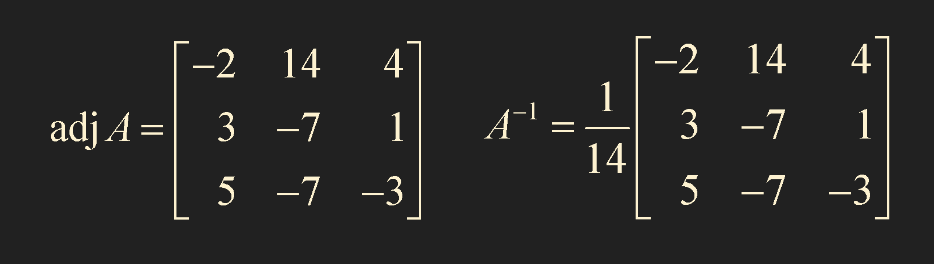용어 정리
- Cramer’s Rule (크레이머,크라메이,크라메르… 난 영어식으로 크래머로 부르겠다. 크래머 공식)
- Inverse formula - 역행렬 공식
- Determinants as area and volumn - 면적과 부피에서의 행렬식
- Linear Trnasformation - 선형 변환
Cramer’s Rule - 크래머의 법칙
- Cramer’s Rule 은 임의의 linear system equation(선형시스템 방정식) 인 Ax=b 의 solution x 를 determinant(행렬식)으로 유도된 공식을 통해 푸는 방법이다.
- 이때 determinant 를 이용하여 해를 풀기 때문에, A는 square matrix (정방 행렬)이어야 하며 singular matrix (특이 행렬)이 아니어야 한다.
- Cramer’s Rule 정의
$ A_i(\mathbf{b}) = [\mathbf{a_1} \dots \mathbf{b} \dots \mathbf{a_n}] $
- $A$ 의 i th column 을 b 로 치환한 것을 $A_i(\mathbf{b})$ 로 표현한다.
Theorem7. Cramer’s Rule
Let $A$ be an invertible $n \times n$ matrix. For any $\mathbf{b}$ in $\mathbb{R}^n$ , the unique solution $\mathbf{x}$ of $A\mathbf{x} = \mathbf{b}$ has entries given by
\[x_i = {\mbox{det} \, A_i(\mathbf{b}) \over \mbox{det} \, A } , \quad \quad i = 1, 2, \dots, n\]
- numerical note : Cramer’s Rule 은 matrix size 가 커질수록 비효율적이므로 유용한 것은 아니다. 따라서, 다른 이론,정리를 유도할 때 주로 사용되는 공식이다.
- 증명
- $A$ 의 column 을 $a_1, \dots. a_n$ 으로 나타내고 identity matrix 인 $I$ 의 column 을 $e_1, \dots, e_n$ 으로 나타내자.
- Ax=b 를 행렬 곱으로 나타내면 다음과 같다.
$ A \cdot I_i(\mathbf{x}) = A [e_1 \quad \dots \quad \mathbf{x} \quad \dots \quad e_n] = [Ae_1 \quad \dots \quad A\mathbf{x} \quad \dots \quad Ae_n] = [a_1 \quad \dots \quad \mathbf{b} \quad \dots \quad a_n] = A_i(\mathbf{b}) $
- 이 때, multiplicatibe property of determinant (table prop9.) 에 의해 다음과 같이 표현할 수 있다.
$ (\mbox{det} \, A)(\mbox{det} \, I_i(\mathbf{x})) = (\mbox{det} \, A_i(\mathbf{b})) $
- $ (\mbox{det} \, I_i(\mathbf{x})) $ 를 cofactor expansion 을 해보면 $x_i$ 가 된다. 따라서 다음과 같이 표현된다.
$ (\mbox{det} \, A) \cdot x_i = (\mbox{det} \, A_i(\mathbf{b})) $
$ x_i = {\mbox{det} \, A_i(\mathbf{b}) \over \mbox{det} \, A } $
- 예시 문제
- Cramer’ Rule 을 사용하여 주어진 방정식을 풀어라
- 고딩때 주구장창 풀던 연립방정식의 해를 구하기 아주 편하고 좋아보인다..
A Formula for $A^{-1}$ - $A^{-1}$ 에 대한 공식
Cramer’s Rule 을 사용하여 $A^{-1}$ 를 명시적인 상태로 표현할 수 있다.
$A^{-1}$ 의 j th column 이 vector x 일때 다음을 만족한다.
- $\mathbf{e}_j$ 는 항등 함수 i 의 j th column 이고, $\mathbf{x}$ 는 $A^{-1}$ 의 j th column 이므로 $x_i$ 는 $A^{-1}$ 의 $(i, j)$ entry 이다.
- 따라서 Cramer’s Rule 에 의해 다음식이 성립한다.
- $A_{ji}$ 가 row j, column i 를 제거한 $A$ 의 부분행렬을 나타내므로, $\mbox{det} \, A_i(\mathbf{e}_j)$ 는 cofactor expansion 으로 다음과 같이 표현가능하다.
- $C_{ji}$ 는 $A$ 의 cofactor 이므로 $A^{-1}$ 의 $(i, j)$ entry 는 $C_{ji}$ 를 $\mbox{det} \, A$ 로 나눈 것과 동일하다.
- 따라서 $A^{-1}$ 를 다음과 같이 표현할 수 있다.
- cofactor 의 matrix 를 수반 행렬 (adjugate or adjoint or classical matrix) 라고 한다.
- 그리고 $\mbox{adj} \, A$ 로 간단히 표현한다.
Theorem8. An Inverse Formula
Let $A$ be an invertible $n \times n$ matrix. Then
\[A^{-1} = {1 \over \mbox{det} \, A} \mbox{adj} A\]
$A^{-1}$ 를 adjugate matrix 로 표현할 수 있다. 이 방식으로 $A^{-1}$ 를 구하는 것은 매우 비효율적이다.
- 예시 문제
- 행렬 A 의 역행렬을 구하라.
- adj A 와 A 를 내적하면 det A 를 구할 수 있다.
Determinants as Area or Volumn - 면적 또는 부피로서의 행렬식
- $\mathbb{R}^2$ 와 $\mathbb{R}^3$ 에 존재하는 어떤 matrix 의 det 는 면적과 부피에 밀접한 관련이 있다.
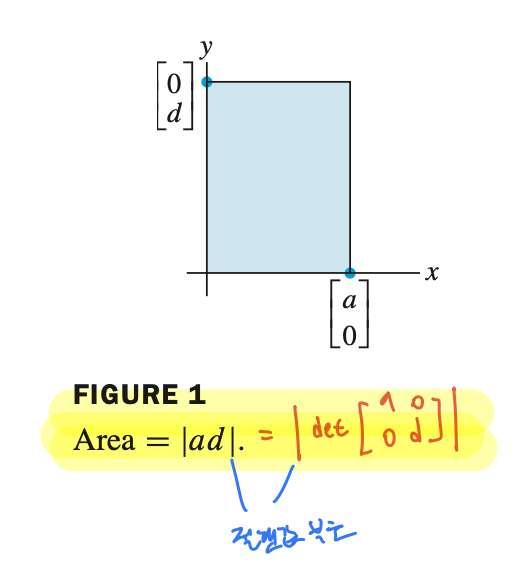
- column 이 (a, 0), (0, d) 인 matrix 의 determinant 는 면적을 의미한다. matrix 의 determinant 가 $ ab - 0 = ab$ 이므로.
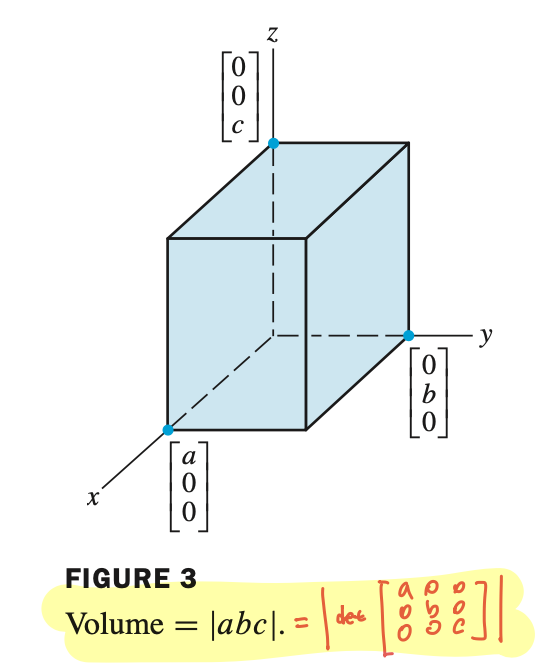
- column 이 (a, 0, 0), (0, b, 0), (0, 0, c) 인 matrix 역시 동일하다. determinant 가 abc 이므로.
Theorem9.
If $A$ is a $2 \times 2$ matrix, the area of the parallelogram(평행 사변형의 면적) determined by the columns of $A$ is $ \left \vert \mbox{det} \, A \right \vert$ . If $A$ is a $3 \times 3$ matrix, the volume of parallelepiped (평행 육면체의 부피) determined by the columns of $A$ is $ \left \vert \mbox{det} \, A \right \vert$ .
$2 \times 2$ 행렬의 det 는 면적이고, $3 \times 3$ 행렬의 det 는 부피이다.
증명
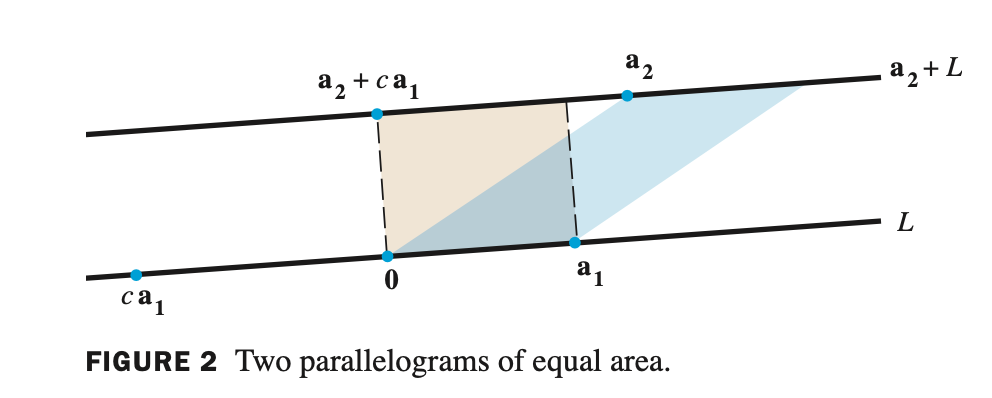
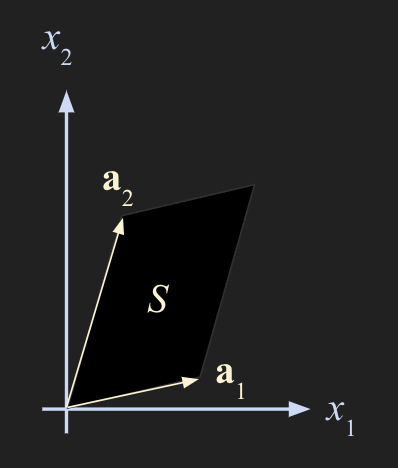
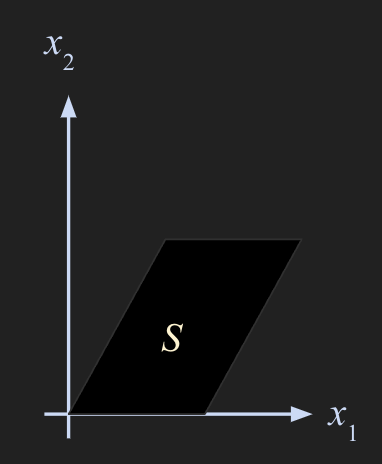
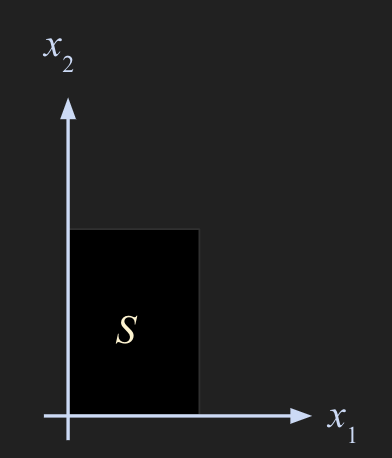
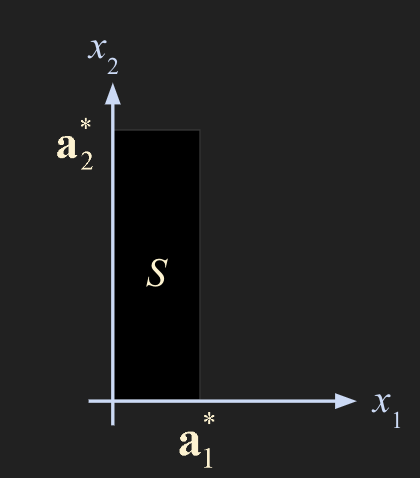
- 평행사변형으로 표현되는 matrix 를 row reduction 연산을 통해 echelon form 으로 변환하면 도형이 standard basis 인 x, y 축에 붙도록 transformation 된다.
ehhelon form 과 pivot 값들은 푸는 사람에 따라 여러가지 결과가 나오지만, 결국 pivot 들의 곱은 항상 동일하므로 det 이 면적을 의미하게 된다.
- 위 방법으로 구하는 것은 row reduction 을 하는 과정을 의미하며 그림으로 설명하면 다음과 같다.
- 예시 문제
- 주어진 행렬의 면적을 구하라.
$ A = \begin{bmatrix} 2 & 6 \\ 5 & 1 \end{bmatrix} $
$ \left \vert \mbox{det} \, A \right \vert = \left \vert 28 \right \vert$
$ = \left \vert 2 - 30 \right \vert = 28 $ , the area of the parallelogram is 28.
- Linear Transformation 에서..
Theorem10.
Let $T$ : $\mathbb{R}^2 \rightarrow \mathbb{R}^2$ be the linear transformation determined by a $2 \times 2$ matrix $A$ . If $S$ is a parallelogram in $\mathbb{R}^2$ , then
\[\{ \mbox{area of } T(S) \} = \left \vert \mbox{det} \, A \right \vert \cdot \{ \mbox{area of } S \}\]If $T$ is determined by a $3 \times 3$ matrix $A , and if $S$ is a parallelepiped in $\mathbb{R}^3$ , then
\[\{ \mbox{volume of } T(S) \} = \left \vert \mbox{det} \, A \right \vert \cdot \{ \mbox{volume of } S \}\]
- $A$ 는 linear transformation 의 standard matrix 를 의미한다.
- $\mathbb{R}^2$ 공간에 존재하는 $S$ 를 $A$ 행렬로 linear transformation 을 한 $T(S)$ 의 면적은 $\mbox{det} \, A \times S$ 의 면적과 동일하다.
- $\mathbb{R}^3$ 공간에 존재하는 $S$ 를 $A$ 행렬로 linear transformation 을 한 $T(S)$ 의 부피는 $\mbox{det} \, A \times S$ 의 부피와 동일하다.
- 증명
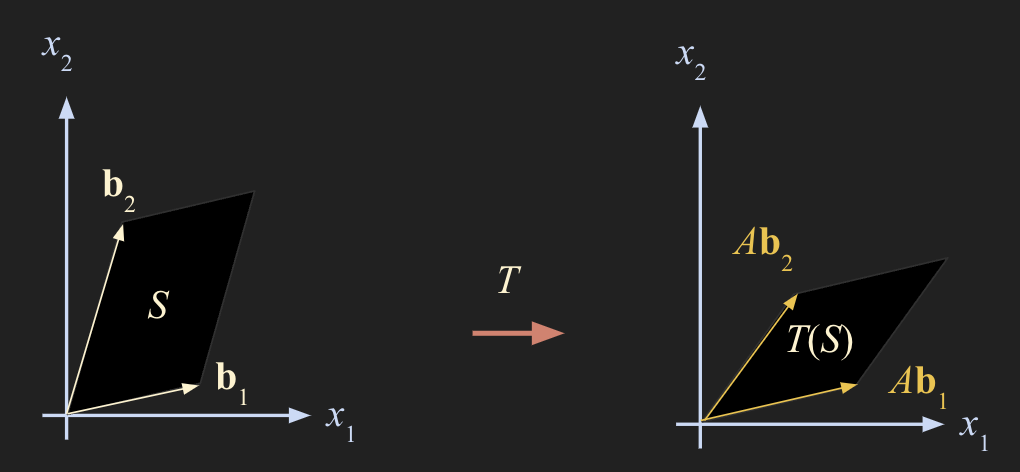
$ S = { s_1\mathbf{b_1} + s_2\mathbf{b_2} : 0 \le s_1 \le 1, 0 \le s_2 \le 1 } $
$ T(s_1\mathbf{b_1} + s_2\mathbf{b_2}) = s_1T(\mathbf{b_1}) + s_2T(\mathbf{b_2}) = s_1A\mathbf{b_1} + s_2A\mathbf{b_2} $
$ [A\mathbf{b_1} A\mathbf{b_2}] = AB $
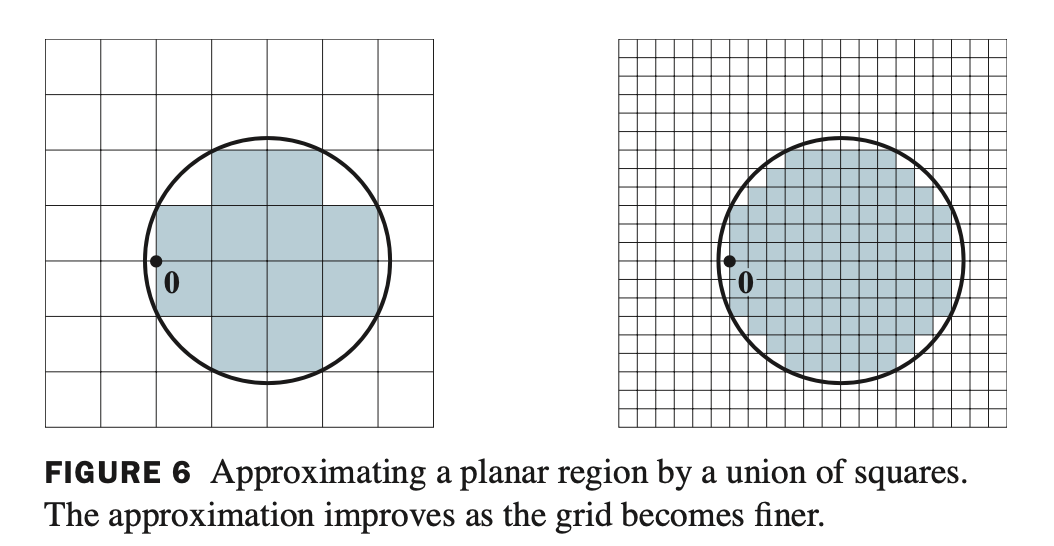
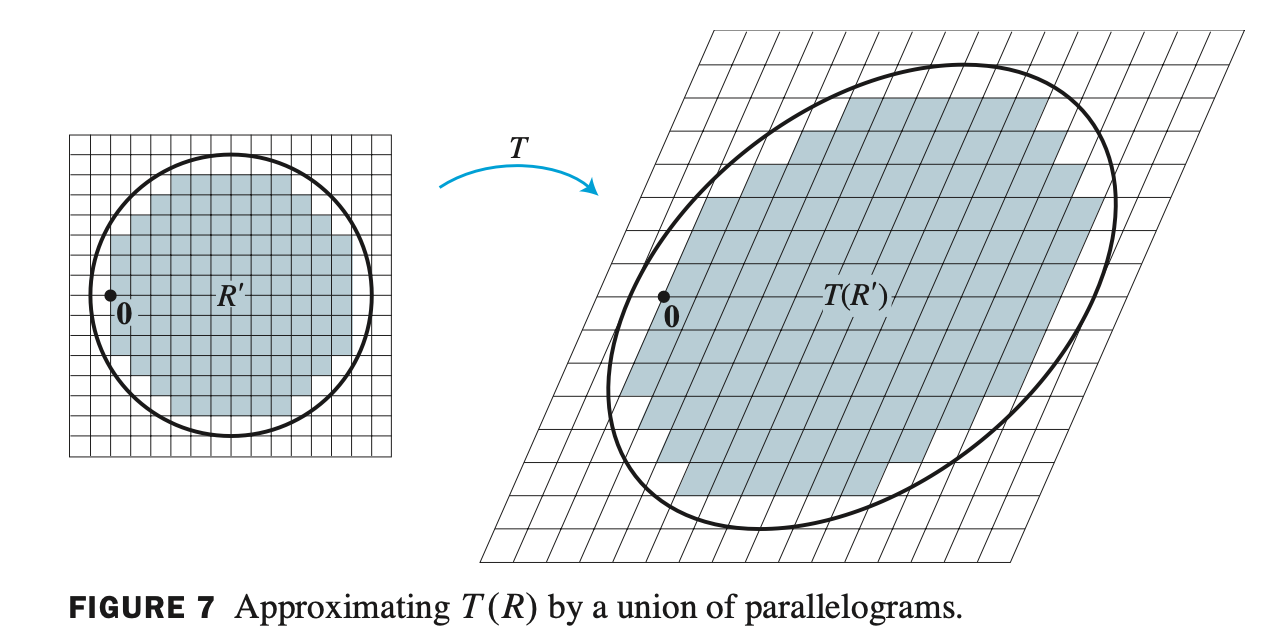
\[\{ \mbox{area of } T(S) \} = \left \vert \mbox{det} \, A \right \vert \cdot \{ \mbox{area of } S \}\]- 여기서 Theorem 10. 은 평행사변형이 아니더라도 임의의 도형에 적용할 수 있다.
- 원을 예시로 들면, 무수히 작은 rectangle 로 원을 표현할 수 있으므로 모든 도형에 적용가능하다.
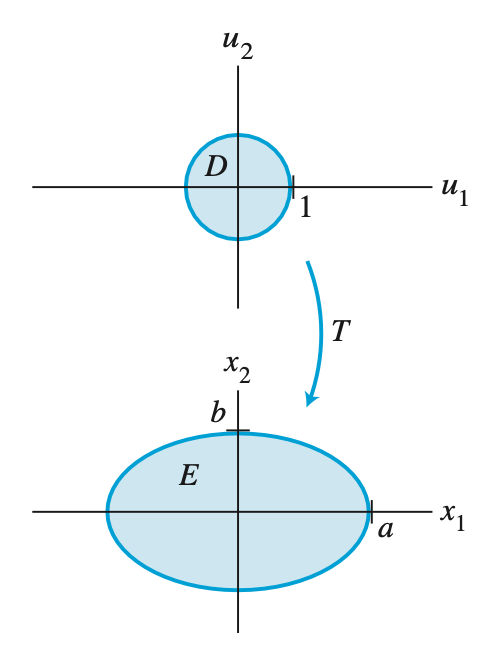
- 예시 문제
- 주어진 타원 방정식의 면적을 구하는 문제.
$ {x_1^2 \over a^2 } + {x_2^2 \over b^2 } = 1 $
- linear transformation 의 standard matrix 인 A 는 다음과 같다.
$ A = \begin{bmatrix} a & 0 \\ 0 & b \end{bmatrix} $
- 따라서 원래 원의 면적인 $\pi$ 와 det A 를 곱하면 $ab\pi$ 가 된다.
$ {\mbox{area of eclipse}} = {\mbox{area of } T(D)} = \left \vert \mbox{det} \, A \right \vert \cdot { \mbox{area of } D } = ab \cdot \pi(1)^2 = \pi ab $