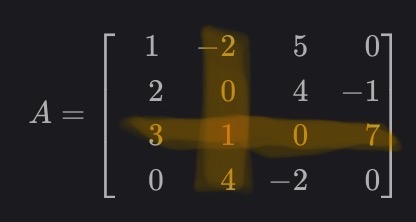Linear Algebra - 3.1 Introduction to Determinants

용어 정리

• determinant (행렬식)
• cofactor (여인수)
• cofactor expansion (여인수 전개)

Determinant - 행렬식

• 역행렬이 아닌 이상 우리는 주로 augmented matrix 를 조합하여 직사각행렬에 대한 계산을 위주로 했었다. 하지만 행렬식 단계에서는 정방행렬에 관련된 내용들이 주이다. 특히 행렬식이 필요한 이유는 여럿 있지만 가장 큰 이유중 한 가지는 Eigen Value (고유값) 때문이다.

• $2 \times 2$ Matrix
• 2장에서 배운 것을 복습하면 $2 \times 2$ 행렬에서의 determinant 가 nonzero 이면 invertible 이다.

\[A = \begin{bmatrix} a_{11} & a_{12} \\\ a_{21} & a_{22} \end{bmatrix}\] \[det \; A = a_{11}a_{22} - a_{12}a_{21}\]

$3 \times 3$ invertible matrix

• $2 \times 2$ 행렬의 determinant 를 구하는 것은 비교적 쉽지만, $3 \times 3$ 행렬 부터 determinant 를 구하는 것은 아주 복잡해진다.
• determinant 가 0이 아닌 것의 의미는 모든 row 에 pivot이 존재한다는 의미이다. 따라서 row reduction 을 진행하고 모든 pivot이 nonzero 임을 확인하면 된다.

\[\begin{bmatrix} a_{11} & a_{12} & a_{13} \\\ a_{11}a_{21} & a_{11}a_{22} & a_{11}a_{23} \\\ a_{11}a_{31} & a_{11}a_{32} & a_{11}a_{33} \end{bmatrix} \quad \sim \quad \begin{bmatrix} a_{11} & a_{12} & a_{13} \\\ 0 & a_{11}a_{22} - a_{12}a_{21} & a_{11}a_{23} - a_{13}a_{21} \\\ 0 & a_{11}a_{32} - a_{12}a_{31} & a_{11}a_{33} - a_{13}a_{31} \end{bmatrix}\] \[A \quad \sim \quad \begin{bmatrix} a_{11} & a_{12} & a_{13} \\\ 0 & a_{11}a_{22} - a_{12}a_{21} & a_{11}a_{23} - a_{13}a_{21} \\\ 0 & 0 & a_{11}\Delta \end{bmatrix}\]

• 여기서 $\Delta$ 는 다음과 같다.
• $\Delta = a_{11}a_{22}a_{33} + a_{12}a_{23}a_{31} + a_{13}a_{21}a_{32} - a_{11}a_{23}a_{32} - a_{12}a_{21}a_{33} - a_{13}a_{22}a_{31}$

• $A$ 가 invertible 이므로, $\Delta$ 는 nonzero 이어야만 한다.

• $2 \times 2$ matrix 에서 determinant 는 아래와 같으므로 $\Delta$ 를 다음과 같이 표기할 수 있다.

• $det A = a_{11}a_{22} - a_{12}a_{21}$

• $\Delta = a_{11} \cdot det A_{11} - a_{12} \cdot det A_{12} + a_{13} \cdot det A_{13}$

• 여기서 예시로 $A_13$ 은 1번째 row 와 3번째 column 을 제외한 요소들을 의미한다.

\[A = \begin{bmatrix} \phantom{-}1 & -2 & \phantom{-}5 & \phantom{-}0 \\\ \phantom{-}2 & \phantom{-}0 & \phantom{-}4 & -1 \\\ \phantom{-}3 & \phantom{-}1 & \phantom{-}0 & \phantom{-}7 \\\ \phantom{-}0 & \phantom{-}4 & -2 & \phantom{-}0 \end{bmatrix}\]

• $A$ 가 위와 같이 주어졌을때, $A_{32}$ 는 다음과 같이 표기가 가능하다.

• 3번째 row 와 2번째 column 을 제거하여 남은 요소들을 행렬로 표현해주면 다음과 같다.

\[A_{32} = \begin{bmatrix} \phantom{-}1 & \phantom{-}5 & \phantom{-}0 \\\ \phantom{-}2 & \phantom{-}4 & -1 \\\ \phantom{-}0 & -2 & \phantom{-}0 \end{bmatrix}\]

For $n \ge 2$ , the determinant of an $n \times n$ matrix $A = [a_{ij}]$ is the sum of $n$ terms of the form $\mp a_{ij}$ det $A_{ij}$ , with plus and minus signs alternating, where the entries $a_{11}, a_{12}, \dots , a_{1n}$ are from the first row of $A$ . In symbols,

$det A = a_{11} \, det A_{11} - a_{12} \, det A_{12} + \dots + (-1)^{1 + n} \, a_{1n} \, det A_{1n} $
$ = \sum\limits_{j=1}^n (-1)^{1 + j} \, a_{1j} \, det A_{1j} $

• 위 시그마 식은 determinant의 정의이다.

determinant 예제

• 다음과 같이 A 행렬이 주어졌을 때 determinant를 구하라.

\[A = \begin{bmatrix} \phantom{-}1 & \phantom{-}5 & \phantom{-}0 \\\ \phantom{-}2 & \phantom{-}4 & -1 \\\ \phantom{-}0 & -2 & \phantom{-}0 \end{bmatrix}\]

\[det A = a_{11} \cdot det A_{11} - a_{12} \cdot det A_{12} + a_{13} \cdot det A_{13}\]

\[det A = 1 \cdot det \begin{bmatrix} \phantom{-}4 & -1 \\\ -2 & \phantom{-}0 \end{bmatrix} - 5 \cdot det \begin{bmatrix} \phantom{-}2 & -1 \\\ \phantom{-}0 & \phantom{-}0 \end{bmatrix} + 0 \cdot det \begin{bmatrix} \phantom{-}2 & \phantom{-}4 \\\ \phantom{-}0 & -2 \end{bmatrix}\]

\[= 1(0 - 2) - 5(0 - 0) + 0(-4 - 0) = -2\]

• determinant 를 다음과 같이 간단히 표현이 가능하다.

\[det A = \vert A \vert = 1 \begin{vmatrix} \phantom{-}4 & -1 \\\ -2 & \phantom{-}0 \end{vmatrix} - 5 \begin{vmatrix} \phantom{-}2 & -1 \\\ \phantom{-}0 & \phantom{-}0 \end{vmatrix} + 0 \begin{vmatrix} \phantom{-}2 & \phantom{-}4 \\\ \phantom{-}0 & -2 \end{vmatrix} = \dots = -2\]

Cofactor - 여인수

• cofactor 를 이용해서 determinant를 여러가지 형태로 표현할 수 있다.

$A = [a_{ij}] , $ the $(i, j)$-cofactor of $A$ is the number $C_{ij}$ given

$C_{ij} = (-1)^{i + j} \, det A_{ij}$

$det A = a_{11}C_{11} + a_{12}C_{12} + \dots + a_{1n}C_{1n}$

• 이를 cofactor expansion (여인수 전개) 라고 한다.

• cofactor 의 부호는 이 식으로 결정되며 $(-1)^{i + j}$ 다음과 같은 규칙을 지닌다.

\[\begin{bmatrix} + & - & + & \dots \\\ - & + & - & \dots \\\ + & - & + & \dots \\\ \vdots & \vdots & \vdots & \ddots \end{bmatrix}\]

Theorem1.

The determinant of an $n \times n$ matrix $A$ can be computed by a cofactor expansion across any row or down any column. The expansion across the $i$ th row using the cofactors in here is

$ det A = a_{i1}C_{i1} + a_{i2}C_{i2} + \dots + a_{in}C_{in}$

The cofactor expansion down the $j$ th column is

$ det A = a_{1j}C_{1j} + a_{2j}C_{2j} + \dots + a_{nj}C_{nj}$

• cofactor expansion 을 이용하면 임의의 row, column 을 선택하여 determinant 를 표현할 수 있다. -> 어떤 cofactor 를 이용하더라도 결과는 동일하다.
• cofactor expansion 을 하기 위해서 zero entry 가 많은 row, column 을 기준으로 설정하면 계산이 단순해진다.

cofactor 예제

• A 가 주어졌을 때, det A 를 cofactor expansion 을 사용해서 구하라.

$ A = \begin{bmatrix} \phantom{-}1 & \phantom{-}5 & \phantom{-}0 \\ \phantom{-}2 & \phantom{-}4 & -1 \\ \phantom{-}0 & -2 & \phantom{-}0 \end{bmatrix} $

$ det A = a_{31}C_{31} + a_{32}C_{32} + a_{33}C_{33} $

$ = (-1)^{3+1} \, a_{31} \, det A_{31} + (-1)^{3+2} \, a_{32} \, det A_{32} + (-1)^{3+2} \, a_{32} \, det A_{32} + (-1)^{3+3} \, a_{33} \, det A_{33} $

$ = 0 \begin{vmatrix} \phantom{-}5 & \phantom{-}0 \\ \phantom{-}4 & -1 \end{vmatrix} - (-2) \begin{vmatrix} \phantom{-}1 & \phantom{-}0 \\ \phantom{-}2 & -1 \end{vmatrix} + 0 \begin{vmatrix} 1 & 5 \\ 2 & 4 \end{vmatrix} $

$ = 0 + 2(-1) + 0 = -2 $

• A 행렬의 determinant 를 구해라
• 0이 많이 구성되어 있는 matrix 는 다음과 같이 cofactor expansion 을 사용할 수 있다.

$ A = \begin{bmatrix} \phantom{-}3 & -7 & \phantom{-}8 & \phantom{-}9 & -6 \\ \phantom{-}0 & \phantom{-}2 & -5 & \phantom{-}7 & 3 \\ \phantom{-}0 & \phantom{-}0 & \phantom{-}1 & \phantom{-}5 & \phantom{-}0 \\ \phantom{-}0 & \phantom{-}0 & \phantom{-}2 & \phantom{-}4 & -1 \\ \phantom{-}0 & \phantom{-}0 & \phantom{-}0 & -2 & \phantom{-}0 \end{bmatrix} $

• first column $A_{11}$ 에 0이 제일 많으므로 이를 기준으로 cofactor expansion 을 사용한다.

$ det A = 3 \cdot \begin{vmatrix} \phantom{-}2 & -5 & \phantom{-}7 & \phantom{-}3 \\ \phantom{-}0 & \phantom{-}1 & \phantom{-}5 & \phantom{-}0 \\ \phantom{-}0 & \phantom{-}2 & \phantom{-}4 & -1 \\ \phantom{-}0 & \phantom{-}0 & -2 & \phantom{-}0 \end{vmatrix} + 0 \cdot C_{21} + 0 \cdot C_{31} + 0 \cdot C_{41} + 0 \cdot C_{51} $

• 또 다시 first column 이 0이 제일 많으므로 이를 이용한다.

$ det A = 3 \cdot 2 \cdot \begin{vmatrix} \phantom{-}1 & \phantom{-}5 & \phantom{-}0 \\ \phantom{-}2 & \phantom{-}4 & -1 \\ \phantom{-}0 & -2 & \phantom{-}0 \end{vmatrix} $

$ det A = 3 \cdot 2 \cdot (-2) = -12 $

• 이 처럼 0 이 많은 row 나 column을 이용하면 아무리 복잡한 행렬이더라도 cofactor expansion 으로 손으로 풀 수 있다.

Theorem2.

If $A$ is triangular matrix, then det $A$ is the product of the entries on the main diagonal of $A$ .

• $A$ 가 triangular matrix (삼각행렬, upper or lower) 이면 det $A$ 는 $A$ 의 diagonal term 을 곱한 것이다.

$ \begin{pmatrix} a_{11} & 0 & 0 \\ a_{21} & a_{22} & 0 \\ a_{31} & a_{32} & a_{33} \end{pmatrix} $ : Lower triangular matrix

$ \begin{pmatrix} a_{11} & a_{12} & a_{13} \\ 0 & a_{22} & a_{23} \\ 0 & 0 & a_{33} \end{pmatrix} $ : Upper triangular matrix

• cofactor expansion 을 이용하여 determinant 를 구하는 것은 매우 복잡한 계산을 해야한다. $n!$ 만큼의 연산이 소요된다.
• 따라서 determinant 를 구하기 위해 cofactor expansion 을 사용하여 계산하는 것은 매우 무모한짓이다.