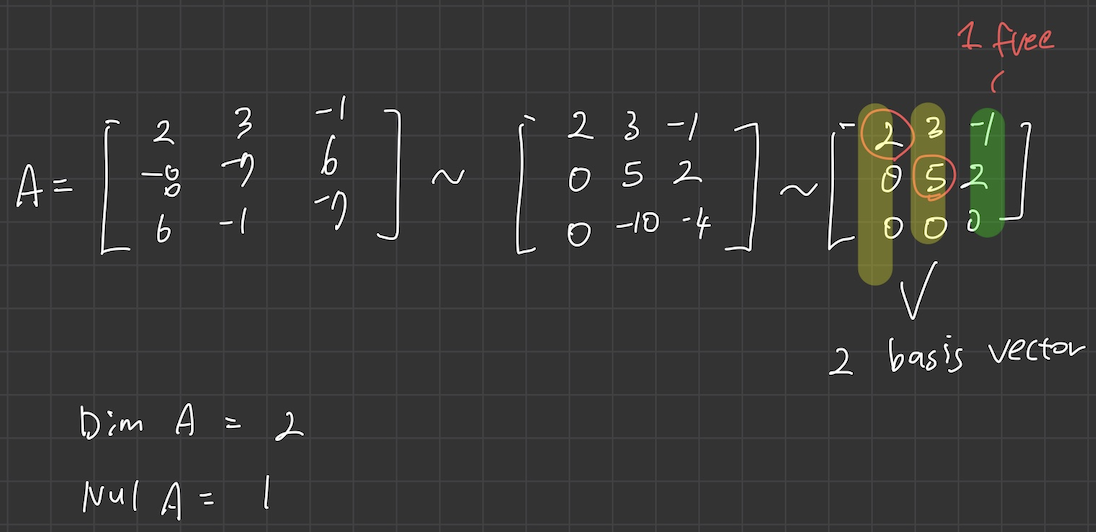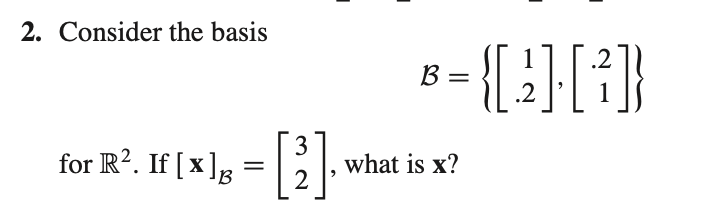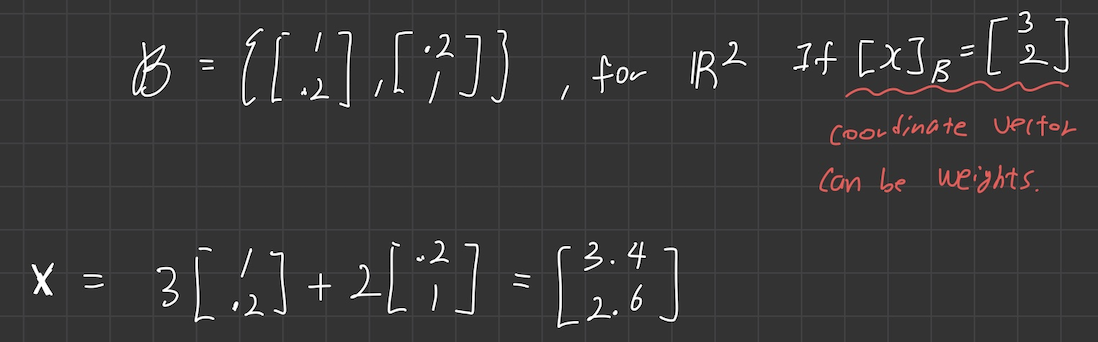용어 정리
- Coordinate system and coordinate vector (좌표계와 좌표벡터)
- Dimension (차원)
- Rank (계수)
Review. Basis for a Subspace - 부분공간에서의 기저
- basis 는 independent set 으로 표현되는 최소한의 vector를 의미한다.
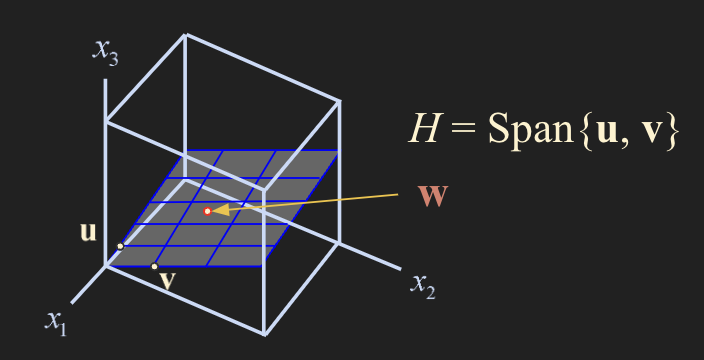
벡터 u,v 는 independent 관계이며 Span{u,v} 는 $\mathbb{R}^3$ 공간에서 2차원 평면을 표시한다.
Span{u,v} 뿐만 아니라 Span{u,w}, Span{v,w} 또한 basis가 될 수 있다. 왜냐하면 u와v, v와w 는 independent 이기 때문이다.
- 즉, basis는 특정 구속조건이 있지 않는한 유일하지 않다 -> basis가 무수히 많이 존재한다.
- 다양한 basis 가 존재할 수 있으며 특정 구속 조건이 있는 경우 이를 standard basis 라고 한다. 각각의 축에 해당하는 단일 크기 vector로 이루어진 것이 standard basis이다.
Coordinate Systems - 좌표계
subspace H 에 존재하는 각각의 vector는 basis vector의 linear combination 으로 표현할 수 있다.
- 증명
- subspace H 에서 basis $\; \mathcal{B} =$ {$b_1, \dots, b_p$} 를 가정하자.
- H 에 있는 vector 는 다음과 같이 생성될 수 있다.
- 두 식을 빼면
- basis 인 $\mathcal{B}$ 가 linearly independent 이므로 각각의 weights 는 0이 되어야 한다. (Ax=0 이므로)
- 즉, 이는 trivial solution 만 존재하므로 scalar 값이 0이 되어야 한다.
- 따라서, $c_j = d_j$ 가 된다.
- basis 가 주어졌을 때 특정 x vector 를 표현하는 weight는 유일하다.
- 예를 들어, $\mathbf{R}^2$ space 의 x,y 좌표계를 standard basis 로 표현하면 [1,0],[0,1] 이 된다.
- [1,1]를 표현하는 방법은 1가지 방s법 밖에 없다.
Coordinates and Coordinate Vector - 좌표와 좌표 벡터
Suppose the set $\; \mathcal{B} =$ {$b_1, \dots, b_p$} is a basis for a subspace $H$ . For each $\mathbf{x}$ in $H$ , the coordinates of $\mathbf{x}$ relative to basis $\mathcal{B}$ are the weights $c_1, \dots, c_p$ such that $\mathbf{x} = c_1\mathbf{b_1} + \dots + c_p\mathbf{b_p}$ , and the vector in $\mathbb{R}^p$
$\quad \quad \quad [ \mathbf{x} ]_{\mathcal{B}} = \begin{bmatrix} c_1 \\ \vdots \\ c_p \end{bmatrix} $
is called the coordinate vector of $\mathbf{x}$ (relative to $\mathcal{B}$) or the $\mathcal{B}$-coordinate vector of $\mathbf{x}$ .
x를 linear combination 으로 표현했을 때 각각의 coordinate($c_1, \dots, c_p$) 를 vector 로 표현한 것이 coordinate vector 이다. 일반 좌표계가 아닌 basis 이기 때문에 linearly independent 이다.
예제
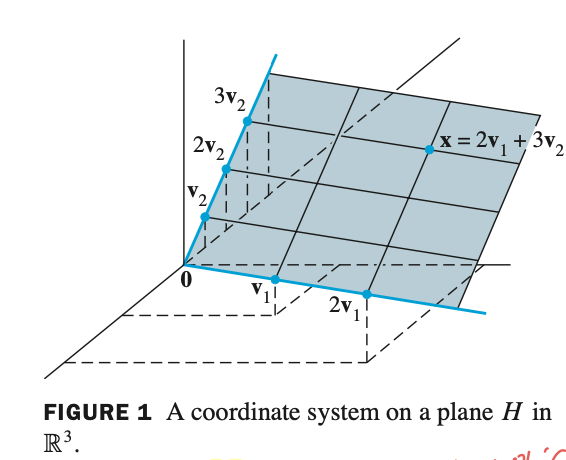
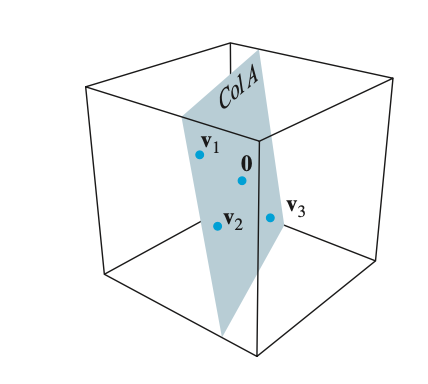
- $v_1, v_2, x$ 가 주어졌을 때, $x$ 를 basis 인 $\mathcal{B}$ 에 대한 coordinate vector 로 표현하는 문제이다.
구하고자 하는 좌표인 $c_1, c_2$ 와 위에 주어진 벡터들을 linear combination 형태로 표현한뒤 row operation 을 진행하면 된다.
위의 row operation 결과 $c_1 = 2$ , $c_2 = 3$ 이 나오고 $x$ 의 coordinate vector 는 다음과 같이 표현된다.
$ [ \mathbf{x} ]_{\mathcal{B}} = \begin{bmatrix} 2 \\ 3 \end{bmatrix} $
위의 좌표계를 기하학적으로 표현하면 다음과 같다.
- 여기서 subspace H 는 $\mathbb{R}^2$ 에 isomorphic (동형 관계)에 있다고 한다.
- basis vector 는 $\mathbb{R}^3$ 에 존재하지만, subspace H 가 마치 $\mathbb{R}^2$ space 에 존재하는 것처럼 동작하기 때문이다. 실제로는 각각의 vector 는 $\mathbb{R}^3$ space 에 있지만, H 는 $\mathbb{R}^2$ 에서 동작하므로 isomorphic 하다고 하는것이다.
- 또한, transformation 은 one-to-one 이다.
- basis set 을 augmented matrix 로 표현 후 row reduction 을 진행하면 column 개수 만큼 pivot 들이 존재한다. (linearly independent 이므로)
- 이는 임의의 b 가 존재할 때 해가 없거나 하나 밖에 없음을 의미하므로 one-to-one 이다.
Dimension - 차원
- 앞서 언급했듯이, basis는 유일하지 않다. n 차원의 space에 대해 무수히 많은 basis가 존재한다. 여기서 차원 (dimension) 은 무엇을 뜻하는것일까?
- 차원 (dimension)은 주어진 공간(space)들에 대한 모든 기저(basis)들은 같은 수의 벡터를 가진다. 여기서 벡터의 수가 바로 그 공간의 차원(dimension)을 의미한다.
- 즉, 차원은 그 공간이 얼마나 큰지를 나타내는 지표이며 기저(basis)가 반드시 가져야할 벡터의 수를 나타낸다. 예를 들어, 4차원 공간의 basis 가 되기 위해서는 반드시 4개의 벡터가 필요하다. 3개는 적고, 5개는 많기 때문에 반드시 4개가 필요한 것이다.
The dimension of a nonzero subspace $H$ , denoted by dim $H$, is the number of vectors in any basis for $H$ . The dimension of the zero subspace {$\mathbf{0}$} is defined to be zero.
- dim H 로 나타내는 nonzero subspace H 의 dimension 은 H 의 basis에 존재하는 vector의 개수 이다.
- 중요한 점!! zero subspace {0} 의 dimension 은 0 이다..!!
zero vector set 은 dependent 이므로 basis가 정의되지 않는다. 따라서 0 dimension 이다.
- 정리하자면 다음과 같다.
A plane through $\mathbf{0}$ (it means origin (0,0)) in $\mathbb{R}^3$ is two-dimensional
A line through $\mathbf{0}$ in $\mathbb{R}^3$ is one-dimensional - 3차원에서 origin(0,0)을 통과하는 평면은 2차원, 3차원에서 origine을 지나는 직선은 1차원을 의미한다.
Rank - 계수
The rank of a matrix $A$ , denoted by rank $A$ , is the dimension of the column space of $A$ .
- matrix A 의 rank 는 A 의 column space 의 dimension 을 의미한다. (pivot position 의 개수라고 봐도 무방하다.)
column space 의 basis vector 가 몇 개 존재하는지? -> dimension 이 된다.
예제
- rank A 와 null A 를 구하라.
우선, matrix A 를 row reduction 을 통해 echelon form 으로 변환하고 pivot column 들을 찾자.
- pivot column 들이 결국 A 의 basis 가 되므로..
- column space 의 dimension rank A 의 개수는 3이다.
- 추가적으로 Null Space 의 dimension 도 구해보자.
- 우선, free variable 이 $x_3, x_5$ 2개 이므로 이를 general solution 으로 나타내면 다음과 같다.
$ x_3\mathbf{u} + x_5\mathbf{v}$
- 즉 우리는 여기서 Ax=0 형태의 homegeneous equation 을 풀면 나오는 general solution 이 null space 이다. 주의할 점은 general solution 의 벡터는 $\mathbb{R}^5$ space 에 있다.
- 따라서, Null Space 의 dimension 은 free variable 의 개수와 같으므로 dim Nul A = 2 이다.
Theorem13. The Rank Theorem
If a matrix $A$ has $n$ columns, then rank $A + $ dim Nul $A = n$ .
- matrix A 가 n 개의 column 을 갖고 있을 때, rank A + dim Nul A = n 이다.
- rank A 는 pivot position 개수, dim Nul A 는 free variable 개수를 의미한다.
Theorem14. The Basis Theorem
Let $H$ be a $p$ -dimensional subspace of $\mathbb{R}^n$ . Any linearly independent set of exactly $p$ elements in $H$ is automatically a basis for $H$ . Also, any set of $p$ elements of $H$ that spans $H$ is automatically a basis for $H$ .
- subspace H 의 dimension 이 p 이고, vector p 개가 있을 때 H 를 Span 하고 있으면 linearly independent 하고 H 의 basis 이다.
혹은 애초에 linearly independent 한 p 개의 벡터들이 subspace H에 있으면 H 의 basis 이다.
- 정리하자면
- H 에서 p 개의 linearly independent set 은 H 에 대한 basis 이다.
p 개의 vector 가 H 를 Span 하고 있으면 H 의 basis 이다.
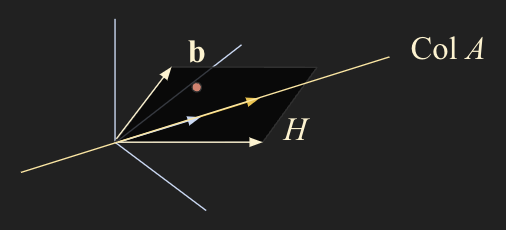
- 위 사진에서 p 개 vector 가 linearly dependent 하면 A 에서 pivot 의 개수는 p 보다 작다.
- 따라서 H 에 존재하는 b 는 Col A 에 존재하지 않는다.
- pivot 이 p 개 보다 적으므로 zero row 가 생기기 때문이다.
- Col A 는 linear combination 을 의미한다.
- 만약 dependent set 인 Col A 에 b 가 만족한다면 Col A는 H를 span 하지 못한다.
- H 가 2개의 linearly dependent vector 로 이루어져있을 때 subspace H 안에 존재하지만 H 를 span 하지는 않는다.
- H 를 span 하려면 linearly independent 가 되어야 하기 때문이다.
The Invertible Matrix Theorem - 추가된 역행렬 정리
- 기존의 역행렬 정리에서 추가되는 정리이다.
The Invertible Matrix Theorem
Let $A$ be an $n \times n$ matrix. Then the following statements are each equivalent to the statement that $A$ is an invertible matrix.
m. The columns of $A$ form a basis of $\mathbb{R}^n$ .
n. Col $A = \mathbb{R}^n$
o. dim Col $A = n$
p. rank $A = n$
q. Nul $A = {\mathbf{0}}$
r. dim Nul $A = 0$
- r 조건을 만족하는 경우는 Ax=0 임을 의미하며 이는 기존 역행렬 정리들이 전부 equivalent 하다는 뜻이다. 따라서 a ~ r 까지 모든 조건이 다 equivalent 하다.
예제
- 주어진 $v_1, v_2, v_3$ 벡터들이 $\mathbb{R}^3$ 의 subspace H 를 span 하므로 basis vector 를 구하기 위해 augmented matrix를 조합하고 row operation 을 진행하면 된다.
- 2개의 pivot position 과 1개의 free variable 이 나왔으므로
- dim $H = 2$ 가 되고 Nul $H = 1$ 이 된다.
H 의 기하학적 표현
예제 2
주어진 좌표 벡터가 있으므로 주어진 basis 와의 linear combination 형태로 표현하여 계산을 진행하면 x 벡터가 도출된다.
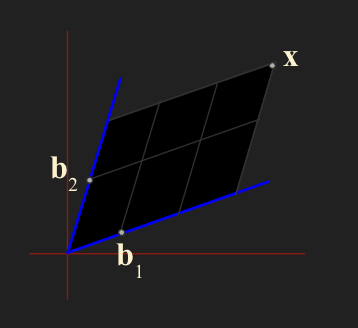
- $b_1, b_2$ 를 basis 를 하는 x 벡터를 표현한 그림이다.
- 여기서 주목할 만한 부분은 $\mathbb{R}^2$ space 에 isomorphic 한 것 그리고 standard basis 형태가 아닌 다른 형태의 basis 를 두 개를 잡아서 표현이 가능하다는 것이다.
예제 3
- 3차원 공간에 4차원의 subspace 를 가질 수 없다. 4차원의 subspace 라는 것은 4개의 indipendent 한 set 이 필요하다는 것인데, 3차원 에서는 3개의 set 밖에 구성할 수 없으므로 impossible 하다.
- $\mathbb{R}^n$ space 의 subspace 를 구성할 수 있는 set 은 n 개 이하인 점을 명심하자.