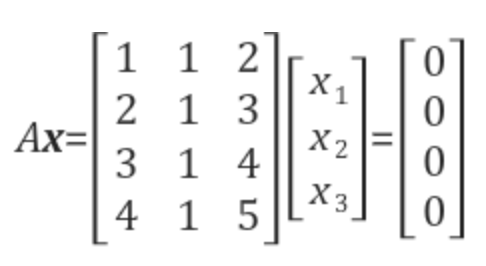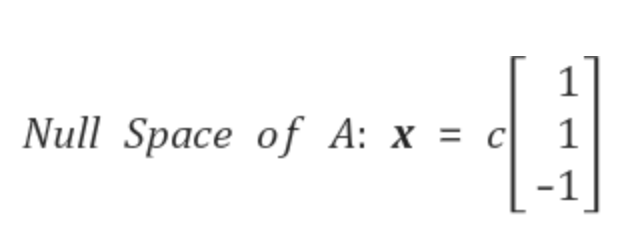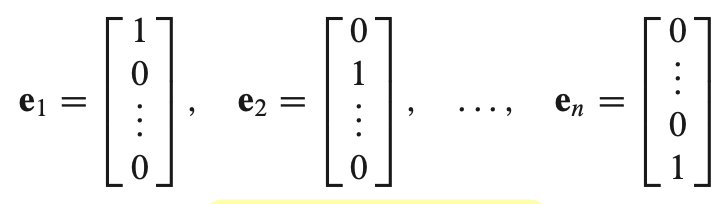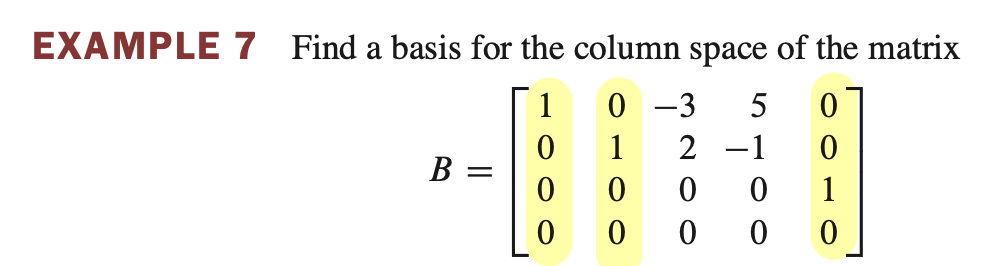Linear Algebra - 2.6 Subspaces of $\mathbb{R}^n$

용어 정리
Subspace of $\mathbb{R}^n$ ($\mathbb{R}^n$ 공간에서의 부분공간)
column space (열 공간)
null space (영 공간)
basis of subspace (부분공간에서의 기저)

Vector Space - 벡터 공간

벡터 공간에서 공간이란 무엇일까? 다수의 벡터들이 존재하고 이들이 모여 하나의 공간을 형성하는 것이다. 다만, 아무 벡터나 혀용되는것이 아니라 이 공간상에 존재하는 벡터들은 서로가 서로에게 더해질 수 있고, 임의의 스칼라값에 곱해져서 벡터가 늘어날 수 있다. 즉, Linear Combination 연산이 같은 공간상에 존재하는 벡터들 사이에 가능하다.
벡터를 표현한 좌표평면계에서는 0벡터가 표현아 되지 않더라도 0 벡터는 공간을 이루기 위해서는 반드시 필요하다. 모든 차원의 벡터공간은 반드시 영벡터를 포함해야한다.

Subspace of $\mathbb{R}^n$ - $\mathbb{R}^n$ 공간에서의 부분공간

A subspace of $\mathbb{R}^n$ is any set H in $\mathbb{R}^n$ that has three properties:
a. The zero vector is in H.
b. For each $\mathbf{u}$ and $\mathbf{v}$ in H, the sum $\mathbf{u} + \mathbf{v}$ is in H.
c. For each $\mathbf{u}$ in H and each scalar c, the vector c$\mathbf{u}$ is in H.
a. zero vector 가 H set 에 존재해야한다.
b. H에 있는 임의의 벡터 $\mathbf{u}$ 와 $\mathbf{v}$ 를 더한 $\mathbf{u} + \mathbf{v}$ 가 H 안에 있어야한다.
c. H에 있는 임의의 벡터 $\mathbf{u}$ 에 스칼라 c 와 곱한 값 c$\mathbf{u}$ 가 H안에 있어야 한다.

subspace (부분공간)를 H 로 표현한다. H 가 위 세 가지 조건에 부합하면 subspace 라고 한다.
subspace 는 scalar multiplication (스칼라 곱) 과 vector addition (벡터 덧셈) 에 closed (닫혀있다.) 되어야 한다고 표현한다.
또한, $\mathbb{R}^n$ 공간에서 zero vectors 를 zero subspace 라고 부른다.

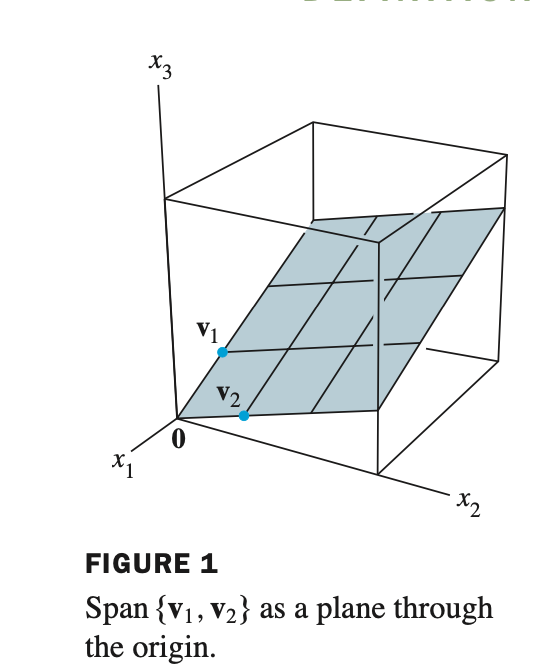
위 그림처럼 Span{$v_1, v_2$} 는 origin (원점)을 지나는 평면인 $\mathbb{R}^3$ 공간의 subspace 가 된다.

Subpsace 예제

증명

$\mathbf{v_1}$ and $\mathbf{v_2}$ are in $\mathbb{R}^n$ and H $ = $ Span{$\mathbf{v_1}, \mathbf{v_2} $}

위 문장을 증명하기 위해 H subspace 에 zero vector 가 포함되어 있어야 한다. 벡터공간에서 설명했듯이 zero vector 는 공간을 이루기위해서는 반드시 필요하므로 다음을 만족한다. $0\mathbf{v_1} + 0\mathbf{v_2} = 0$ 이말인 즉슨, $0\mathbf{v_1} + 0\mathbf{v_2}$ 는 $\mathbf{v_1}, \mathbf{v_2}$ 의 선형결합임을 만족한다.

$ \mathbf{u} = s_1\mathbf{v_1} + s_2\mathbf{v_2} \quad $ and $ \quad \mathbf{u} = t_1\mathbf{v_1} + t_2\mathbf{v_2}$

Span{$\mathbf{v_1}, \mathbf{v_2} $} 는 선형결합이므로, $\mathbf{v_1}, \mathbf{v_2} $ 에 임의의 스칼라값을 곱해 덧셈 연산을 한 벡터 또한 $\mathbf{v_1}, \mathbf{v_2} $ 의 선형결합 이므로 다음 식을 만족한다.

$\mathbf{u} + \mathbf{v} = (s_1 + s_2)\mathbf{v_1} + (t_1 + t_2)\mathbf{v_2}$

따라서 $\mathbf{u} + \mathbf{v}$ 는 $\mathbf{v_1}, \mathbf{v_2}$ 의 선형결합이고 H subspace 임을 만족한다.

마찬가지로 scalar multiplciation 에 대해서도 확인해보자.

$ c\mathbf{u} = c(s_1\mathbf{v_1} + s_2\mathbf{v_2}) = (cs_1)\mathbf{v_1} + (cs_2)\mathbf{v_2}$

위 식을 만족하므로 $c\mathbf{u}$ 는 H subspace 임을 만족한다.

위 조건들을 일반화 시켜보면 $\mathbb{R}^n$ space 에 있는 $v_1, v_2, \dots, v_p$ 벡터들이 주어졌을 때, Span{$v_1, v_2, \dots, v_p$} 는 $\mathbb{R}^n$ 의 subspace 이다.

Geometrical Comfirmation

좌측 그림을 보면, $\mathbb{R}^2$ space 에서 직선 L은 origin (0,0) 을 지나지 않는다. 이는 L이 zero vector를 포함할 수 없다는 것을 의미한다. 또한, $\mathbf{u} + \mathbf{v}$ 벡터의 덧셈 또한 L에 존재하지 않으며, 우측 그림에서 scalar mutliplication 도 직선 L에 존재하지 않으므로 subspace 가 아니다.

Column Space - 열 공간

The column space of a matrix A is the set Col A of all linear combinations of the columns of A.

Column Space 도 Subspace 이다.
column space 를 Col A라고 표현한다. column space는 matrix A 의 column 들의 모든 linear combination (선형 결합)을 의미한다.
즉, 임의의 행렬 A 에서 모든 column 들의 linear combination (선형 결합)은 subspace (부분공간)을 형성한다. 우리는 이를 column space라고 부른다.
$\mathbb{R}^m$ 공간에서 $A = [a_1, \dots, a_n]$ 으로 주어졌을 때 Col A $=$ Span{$a_1, \dots, a_n$} 이다.
즉, A의 열들을 Span 한 것이 열 공간 (column space) 이며 $\mathbb{R}^m$의 부분 공간(Subspace)이다.

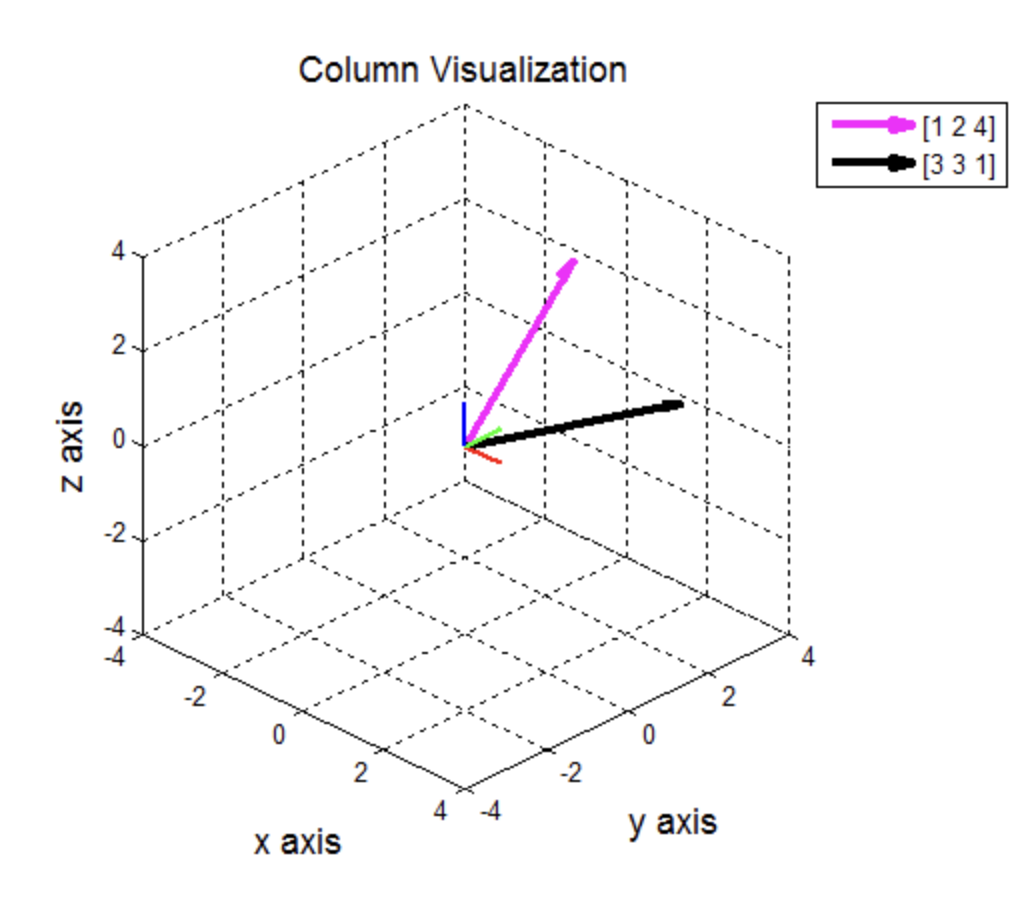
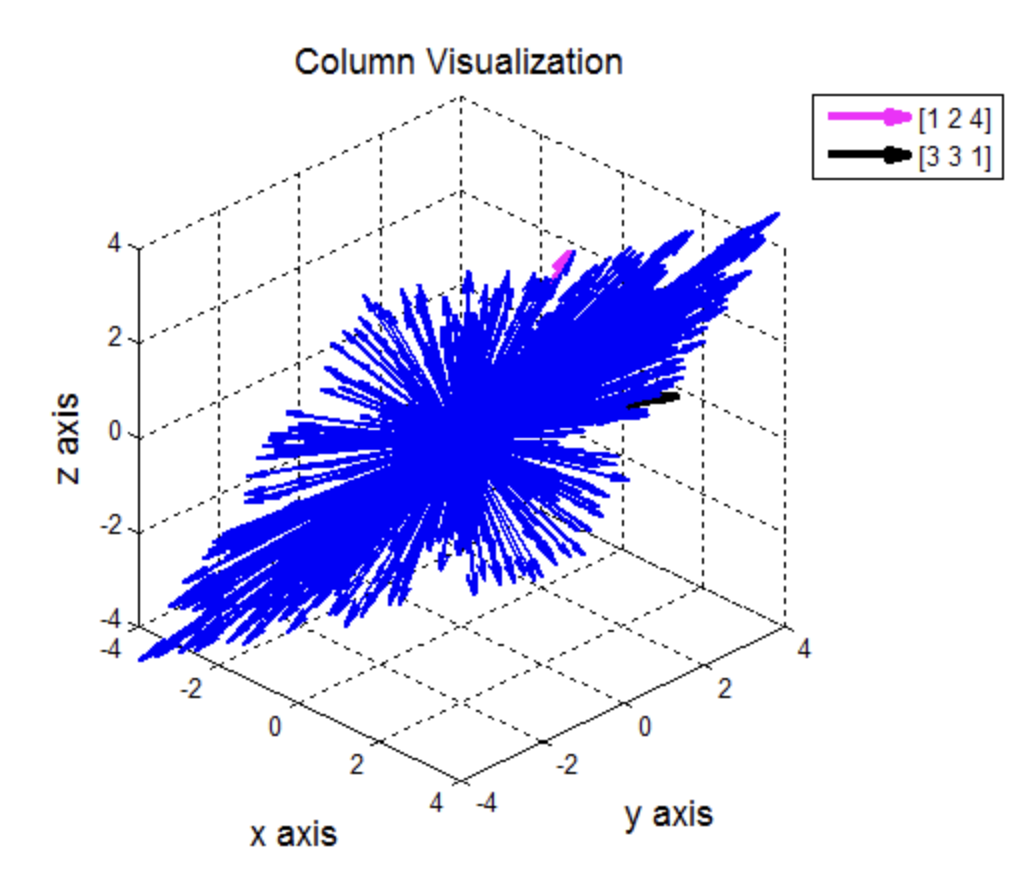
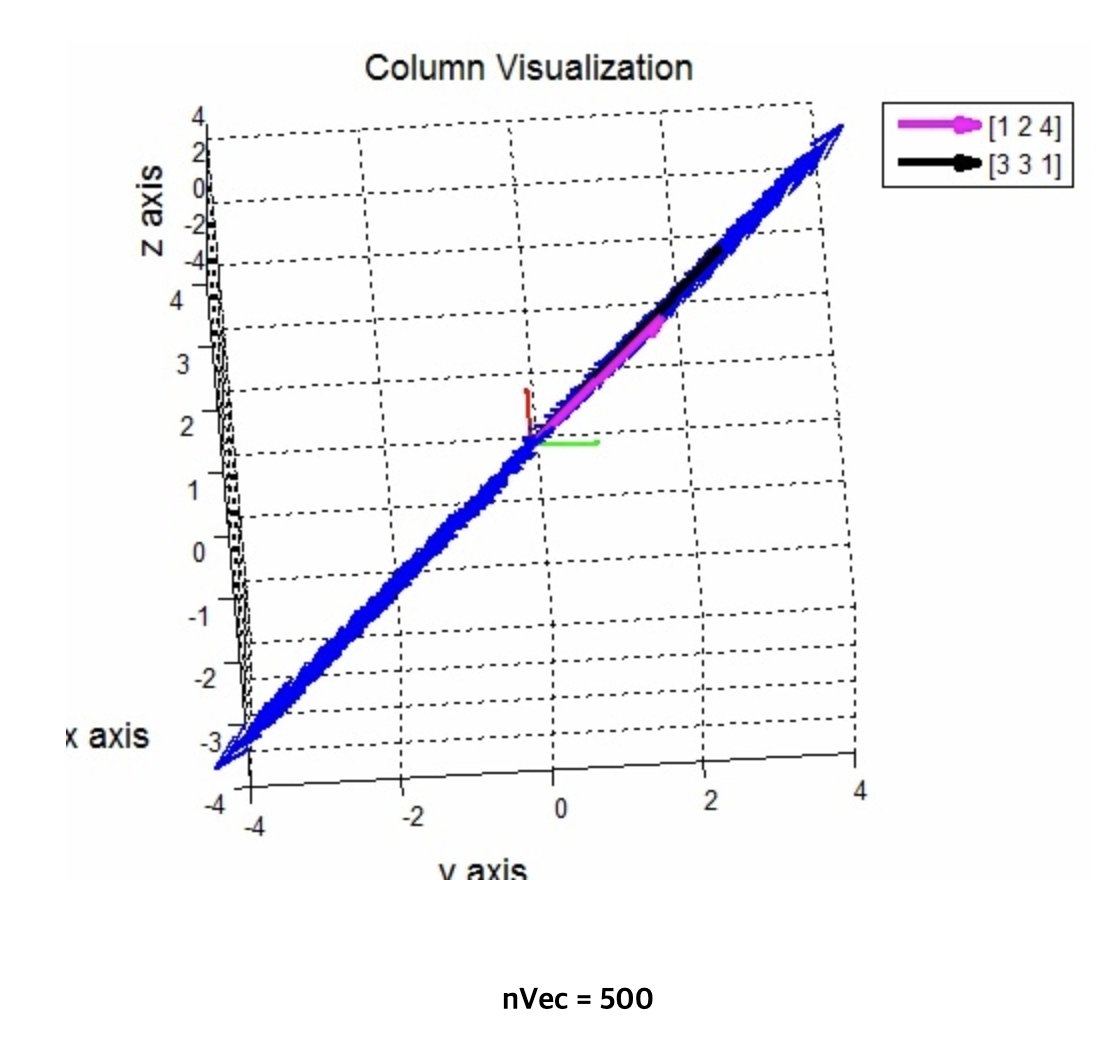
위 사진은 선형 결합을 10개 정도 실행한 결과이다.

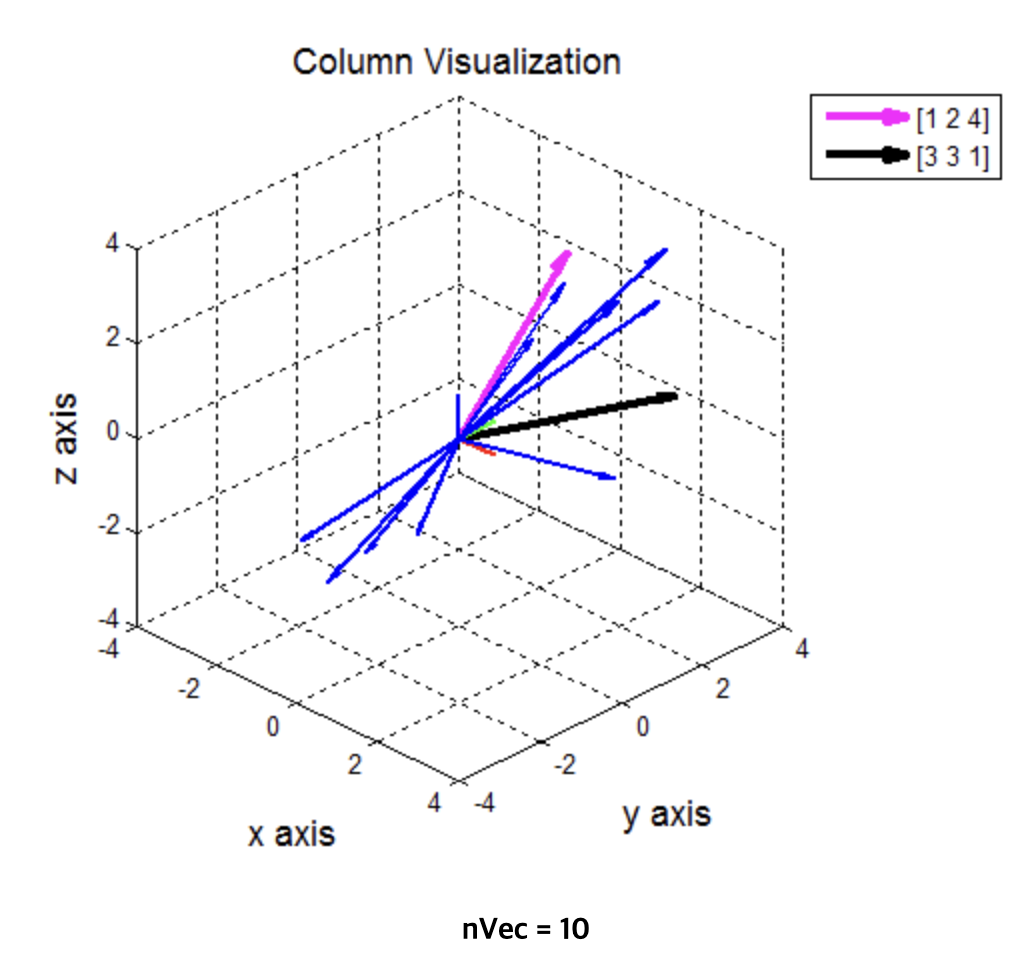
선형 결합을 500개 까지 실행한 결과, 평면의 형상이 나온다.
결론적으로 행렬 A의 column 들의 linear combination 을 통해 \mathbb{R}^3 의 subspace가 평면(plane)이라는 것을 확인할 수 있다.
subspace 를 정의하기 위해선 임의의 행렬 A의 column 원소들의 가능한 모든 선형 조합을 생각하면 된다.

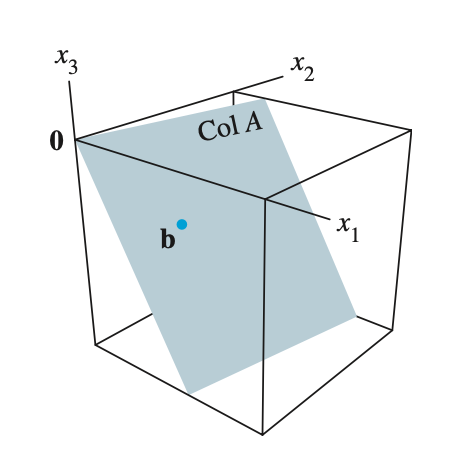
Is b in Col A? - 열 공간 A에 b가 존재하는가?

이는 $A\mathbf{x} = \mathbf{b}$ 가 consistent 한지 를 의미한다.

우리는 선형 방정식 $A\mathbf{x} = \mathbf{b}$ 에 대해 b 벡터가 A의 column space에 존재할 때에만 해를 구할 수 있다. 즉 b 벡터가 A의 column의 선형 결합으로 표현이 가능할 때 $A\mathbf{x} = \mathbf{b}$ 에 대한 해를 구할 수 있다. 결국 b 가 행렬 A의 column space 에 존재해야만 해를 구할 수 있다.
$A\mathbf{x} = \mathbf{b}$ 형태는 nonhomogeneous system 이라는것을 의미하며 벡터b는 nonzero vector 임을 의미하며 적어도 하나의 entry 는 nonzero 이어야한다.
예시 문제를 살펴보자.

echelon form 을 만들기 위해 행렬A와 b를 augmented matrix 로 조합한 뒤 row reduction 을 진행한다.
여기서는 pivot position 이 2개이고 $x_3$ 는 free variable 인 것을 알 수 있다. 이말인 즉슨 infinitely many solution이므로 consistent 함을 알 수 있다.
따라서 해가 존재하므로 -> b는 행렬 A의 column space 에 존재한다.

Null Space - 영 공간

The null space of a matrix $A$ is the set Null $A$ of all solutions of the homogeneous equation $A\mathbf{x} = 0$ .

행렬 A의 null space (영 공간)는 homogeneous equation $A\mathbf{x} = 0$ 의 모든 해의 집합을 의미한다. 이를 Null A 로 표현한다.
Null Space 는 앞의 Column Space 와는 완전힌 다른 Subspace 이다.

Theorem12.
The null space of an $m \times n$ matrix $A$ is a subspace of $\mathbb{R}^n$ . Equivalently, the set of all solutions of a system $A\mathbf{x} = 0$ of $m$ homogeneous linear equations in $n$ unknowns in a subspace of $\mathbb{R}^n$.

$m \times n$ 행렬 A의 null space 는 $\mathbb{R}^n$ space 의 subspace 이다.
동일하게, n 개의 미지수를 갖고있는 m개의 homogeneous euqation 인 $A\mathbf{x} = 0$ 의 모든 해의 집합은 $\mathbb{R}^n$ 공간의 subspace 이다.
증명
subspace 의 3가지 조건을 만족하는지 살펴보자.
homogeneous equation 은 $A\mathbf{x} = 0$ 를 만족하므로 a 조건을 만족한다. (zero vector 가 subspace 에 존재하는지?)

\[A(\mathbf{u} + \mathbf{v}) = A\mathbf{u} + A\mathbf{v} = 0 + 0 = 0\]

위 식을 통해 벡터의 덧셈 또한 subspace에 존재한다.

\[A(c\mathbf{u}) = c(A\mathbf{u}) = c(0) = 0\]

위 식을 통해 스칼라 곱 또한 subspace 에 존재한다.
따라서 null space는 3가지 subspace 조건에 부합하므로 $\mathbb{R}^n$ 의 subspace 임을 증명할 수 있다.
정리하자면, $A\mathbf{x} = 0$ 의 해들이 이루는 공간을 Null Space 라고 한다. 즉 어떤 Null Space 든지 반드시 zero vector를 포함한다.

Geometrical Comfirmation

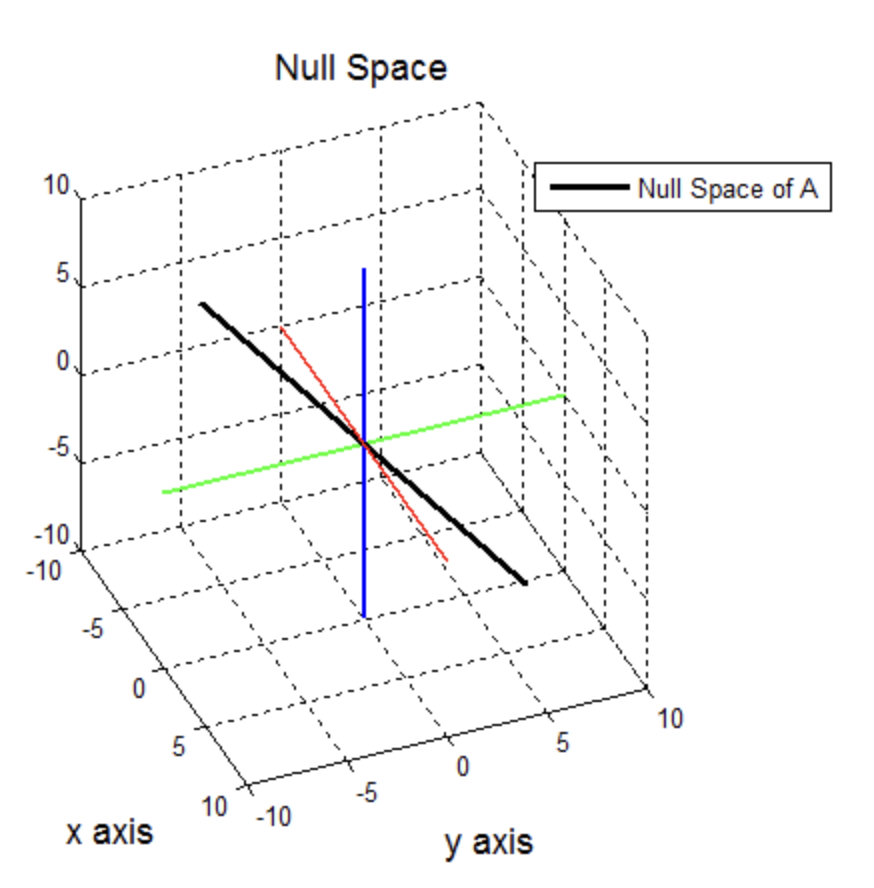
위 의 과정을 통해 Null Space 를 정의한 뒤 3차원 공간에 표현해보면

위와 같이 3차원 공간에서 Null Space 는 직선 형태로 표현된다.
그림처럼 zero vector (origin) 과 x = [1 1 -1] 을 지나는 직선으로 정의된다. 이것이 3차원 공간의 subspace 인 A의 Null Space 이다.

Basis for a Subspace - 부분공간에서의 기저

A basis for a subspace $H$ of $\mathbb{R}^n$ is a linearly independent set in $H$ that spans $H$.

$\mathbb{R}^n$ 공간의 subspace H에 대한 basis (기저)는 H를 Span 하는 linearly independent 집합이다.
이말인즉슨, 기저 벡터들은 independent 하다. 기저 벡터들은 space 를 span 한다라고 볼 수 있다.
위 내용을 기하학적으로 확인해보자. 다음과 같은 (1) (2) 두 개의 식이 3차원 공간상에 존재한다고 하자.

$ \begin{bmatrix} 1 \\ 1 \\ 2 \end{bmatrix} \; , \; \begin{bmatrix} 2 \\ 2 \\ 5 \end{bmatrix} \; , \; \begin{bmatrix} 3 \\ 3 \\ 7 \end{bmatrix} \quad \dots (1)$

$ \begin{bmatrix} 1 \\ 1 \\ 2 \end{bmatrix} \; , \; \begin{bmatrix} 2 \\ 2 \\ 5 \end{bmatrix} \; , \; \begin{bmatrix} 3 \\ 4 \\ 8 \end{bmatrix} \quad \dots (2)$

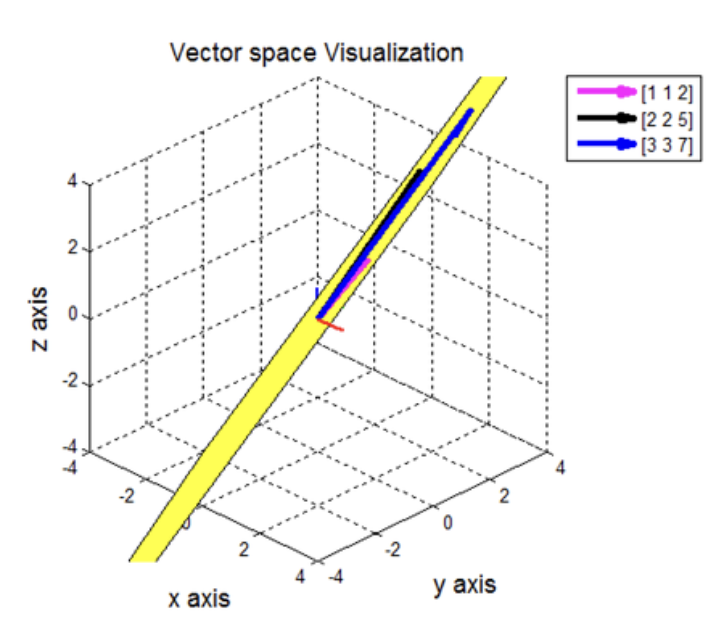
식 (1) 의 경우 세 번째 벡터가 첫 번째, 두 번째 벡터의 합이므로 dependent 하다. 이는 세 번째 벡터 [3 3 7] 은 첫 번째와 두 번째 벡터가 이루는 평면 상에 존재하는 것이다. 따라서 3차원 공간 전체를 span 하지 않는다.
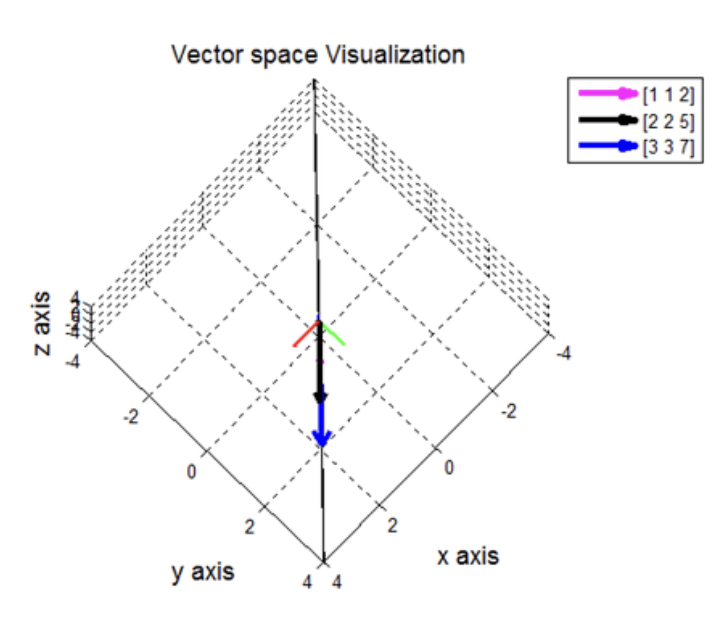
식 (2) 의 경우 세 개의 3차원 column vector 로 이루어져있고, 서로 독립이다. 이는 3차원 공간 전체를 span 하므로 $\mathbb{R}^3$ 의 basis 이다.

위 그림에서 노란색 부분이 식 (1) 의 column space 를 표현한 것이다. 평면임을 확인할 수 있고 세 번째 벡터가 첫번째,두번째 벡터가 이룬 평면위에 놓여있음을 알 수 있다. 따라서 식 (1) 은 linearly dependent 하다.

Standard Basis for $\mathbb{R}^n$ - $\mathbb{R}^n$ 공간에서 표준 기저

Standard Basis (표준 기저) 는 invertible 한 $n \times n$ identity matrix (항등 행렬) 에서 각각의 column을 갖고 온것이다.

$e_1, \dots, e_n$ 집합을 $\mathbb{R}^n$ 공간에서의 표준 기저 (standard basis) 라고 한다. identity matrix 의 열 집합이므로 linearly independent 집합이다.

기저를 찾는 예제
예제(1) $\quad$ A행렬의 영 공간에 대한 기저를 찾아라.

null space 에서의 basis 를 찾는 문제이므로 Ax=0 의 solution 을 구한다.
pivot position 을 통해 $x_2, x_4, x_5$ 는 free variable 이고 $x_1, x_3$ 는 basic variable 임을 확인할 수 있다.
이를 General Solution 으로 풀면 $x_2u + x_4v + x_5w$ 이고 $x_2u + x_4v + x_5w = 0$ 을 풀면 $x_2, x_4, x_5$ 가 free variable 이므로 trivial solution 만 존재한다.
이는 {u,v,w} 가 linearly independent 임을 의미한다. 따라서 {u,v,w} 가 null space 에서의 basis 이다.
homogeneous equation 의 general solution 은 null space 의 basic vector의 linear combination 으로 표현된다.

예제(2) $\quad$ 열 공간에 대한 기저를 찾아라.
column space 는 행렬의 모든 column 을 span 한 것을 의미한다.
문제에서 묻는 것은 최소한의 linearly independent set 을 찾고자 하는 것이다.

reduced echelon form 으로 변환하면 pivot column 을 찾을 수 있다.
pivot column 간 linearly independent 가 성립하므로 {b_1, b_2, b_5} 가 Col B를 span 하고 basis 이다.

여기서 pivot column 이 아닌 column 들 ($b_3, b_4$) 은 pivot column 으로 표현이 가능하다.
각각의 column vector 는 identity matrix 에 있는 column vector의 일부이다. -> reduced echelon form 이므로
따라서 $b_1, b_2, b_5$ 는 linearly independent 이고 나머지 $b_3, b_4$ 는 $b_1, b_2, b_5$ 의 set 으로 표현된다.

예제(3) $\quad$ 열 공간에 대한 기저를 찾아라.

주의, row operation은 행렬의 열들의 선형 종속 관계에 영향을 주지 않는다.
위 행렬을 row operation 을 통해 echelon form 으로 만들면 $a_1, a_2, a_5$ 가 pivot column 인 것과 이 column 들은 linearly independent 임을 확인할 수 있다.
따라서 A 의 column space 의 basis 는 $a_1, a_2, a_5$ 이며 {a_1, a_2, a_5} spans Col A 이다.

주의할 점은 echelon form 의 pivot column 이 basis 가 아니라 원래 형태 행렬의 pivot column 이 basis 이다.
즉, Col A $ \ne $ Col B 이다.
모든 row 가 pivot을 갖고 있는 경우만 Col A $ = $ Col B 가 성립하며, 이는 subspace 가 space 전체임을 의미한다.

Theorem13.
The pivot columns of a matrix $A$ form a basis for the column space of $A$ .
행렬 $A$ 의 pivot column 들은 $A$ 의 column space 의 basis 이다.

Warning.
Be careful to use pivot columns of $A$ itself for the basis of Col $A$ . The columns of an echelon form $B$ are often not in the column space of $A$ .
For instance, in 예제 (2),(3), the columns of $B$ all have zeros in their last entries and cannot generate the columns of $A$ .