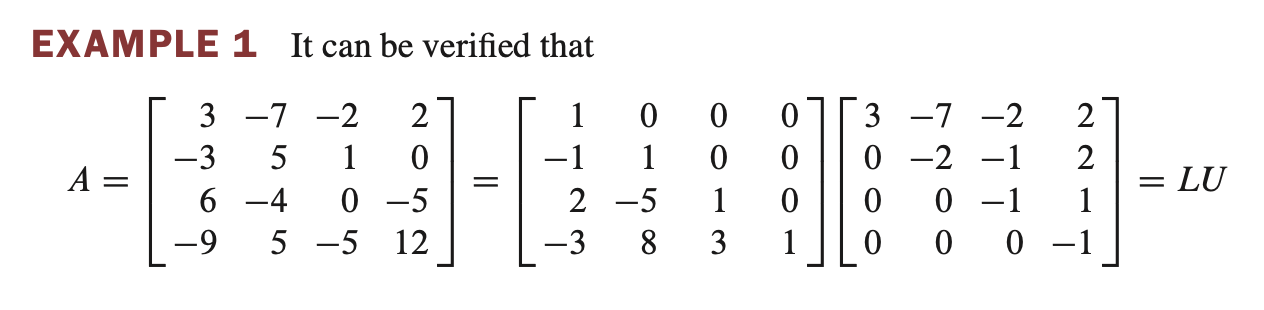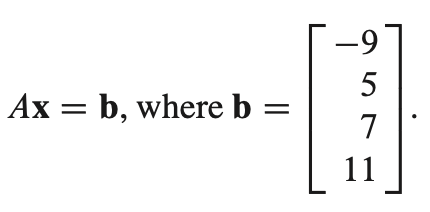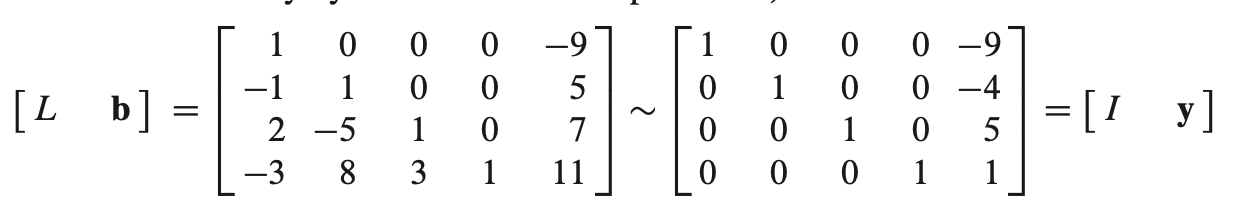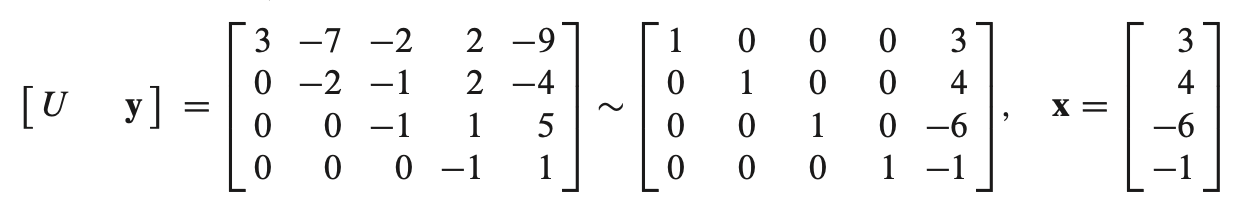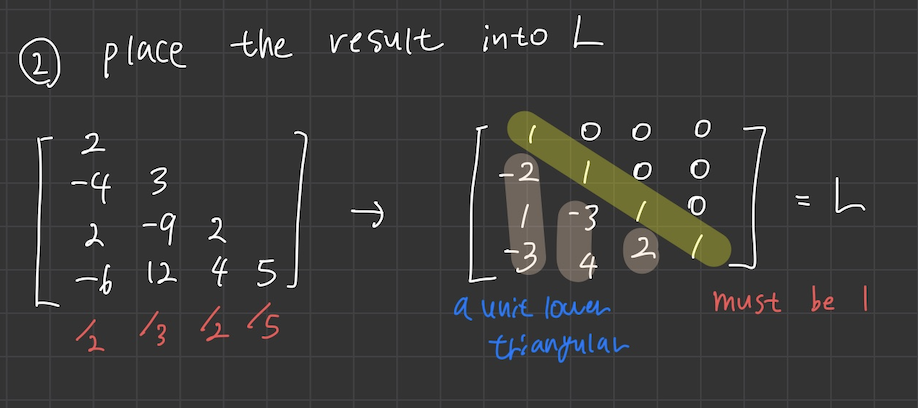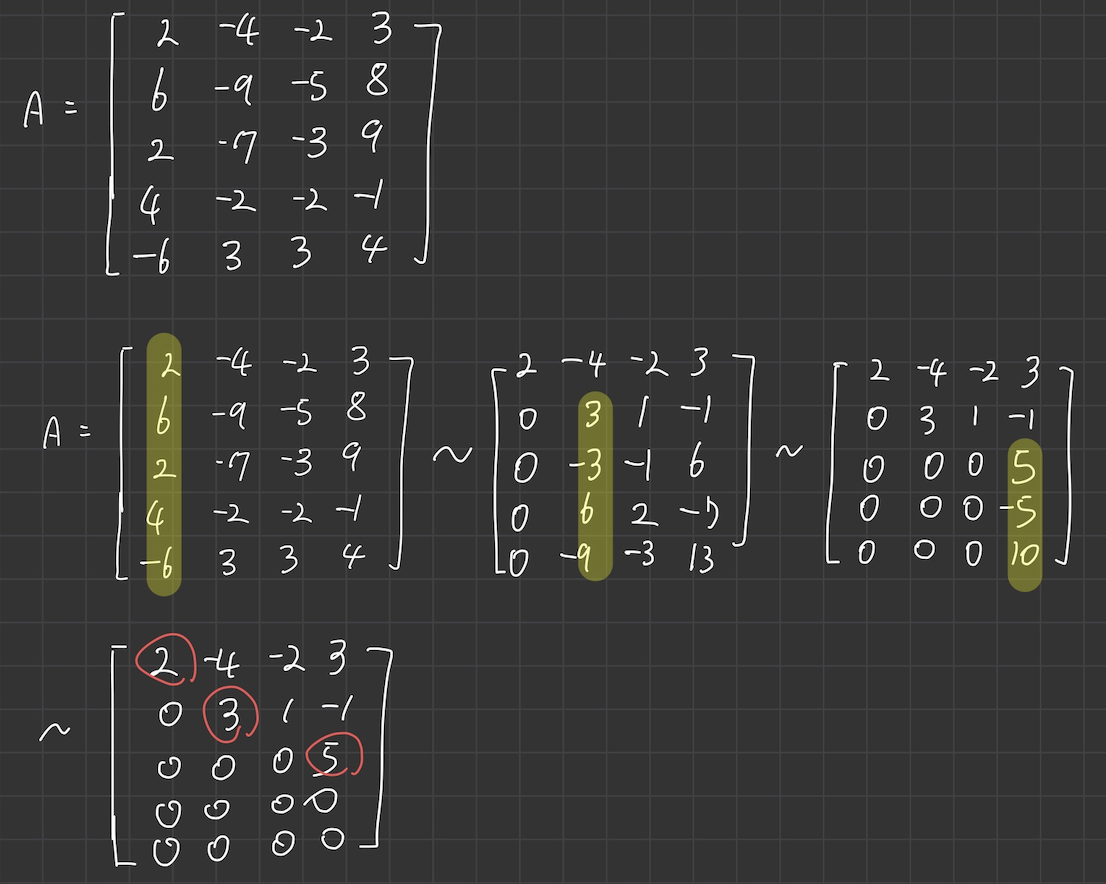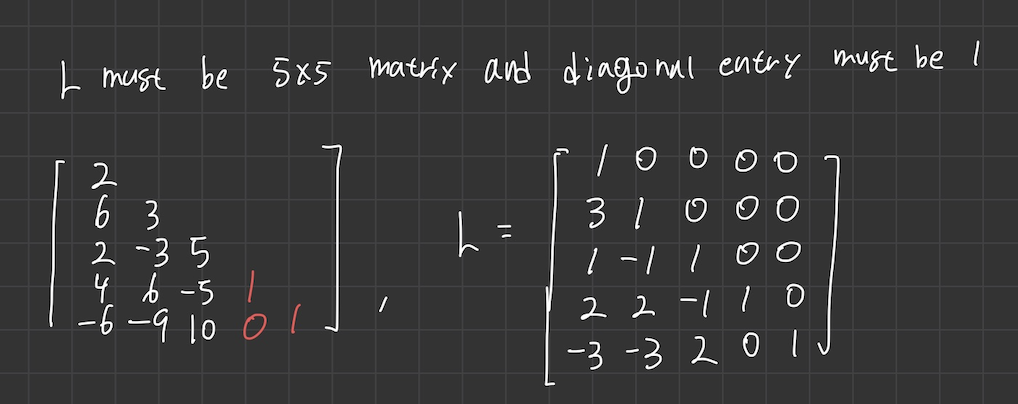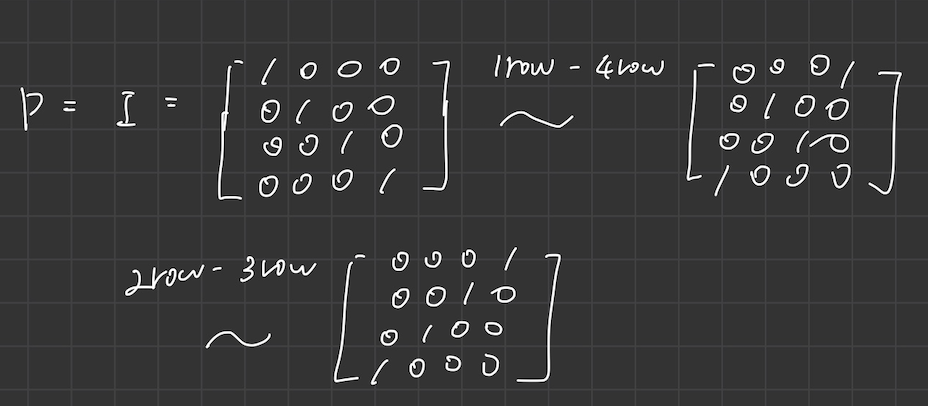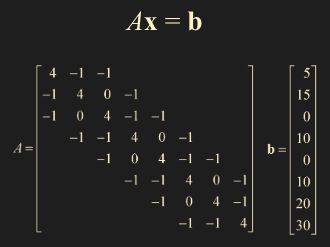Linear Algebra - 2.5 Matrix Factorizations, LU Decomposition

용어 정리
LU Decomposition (LU 분해)
PA = LU 에서 P 는 Permutation Matrix (치환행렬) - A의 행을 조작(interchange)하기 위한..

Factorization, Decomposition - 분해

factorization 은 하나의 행렬을 두 개 혹은 세 개 이상의 행렬 곱으로 표현한 식을 의미한다.

\[A = BC\]

A 행렬을 B와 C의 곱으로 표현했는데, 이런 형태를 분해(factorization) 이라고 한다.

LU decomposition - LU 분해

\[A\mathbf{x} = \mathbf{b_1}, \quad A\mathbf{x} = \mathbf{b_2}, \quad \dots \quad A\mathbf{x} = \mathbf{b_p},\]

방정식을 푸는 방식은 크게 두 가지가 있다.

(1) $A$ 의 역행렬을 이용
이 경우에 $A^{-1}\mathbf{b_1}, A^{-1}\mathbf{b_2}$ 모든 경우를 구해야 하므로 비효율적이다.

(2) LU decomposition
row reduction 으로 $A$ 를 LU 분해하여 방정식을 푸는 것이 빠르고 효과적이다.

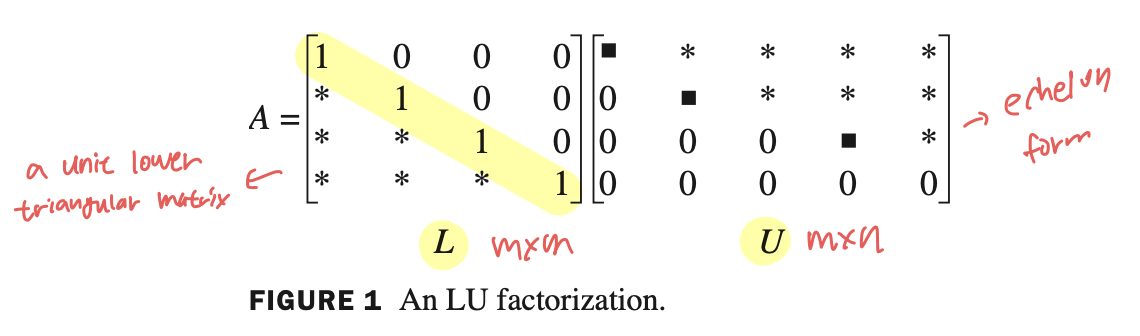
L 은 a unit lower triangular matrix 를 의미한다.
L의 diagonal term 들은 모두 1 이고 대각선 아래는 nonzero entry 인 행렬이다. nonzero entry 에 0이 들어가도 상관없다. 반대로 위쪽은 무조건 0이 되어야한다.
diagonal term 이 모두 1이어야만 하는 이유는 1이 아닐 때 너무 다양한 값이 도출되기 때문이다.
U 는 echelon form 을 의미한다. 절대로 reduced echelon form 이 아닌것을 명심하자.

A 를 분해해서 U로 변환할 때 row interchange, scaling 없이 오로지 replacement 만을 사용해서 변환을 해야한다.

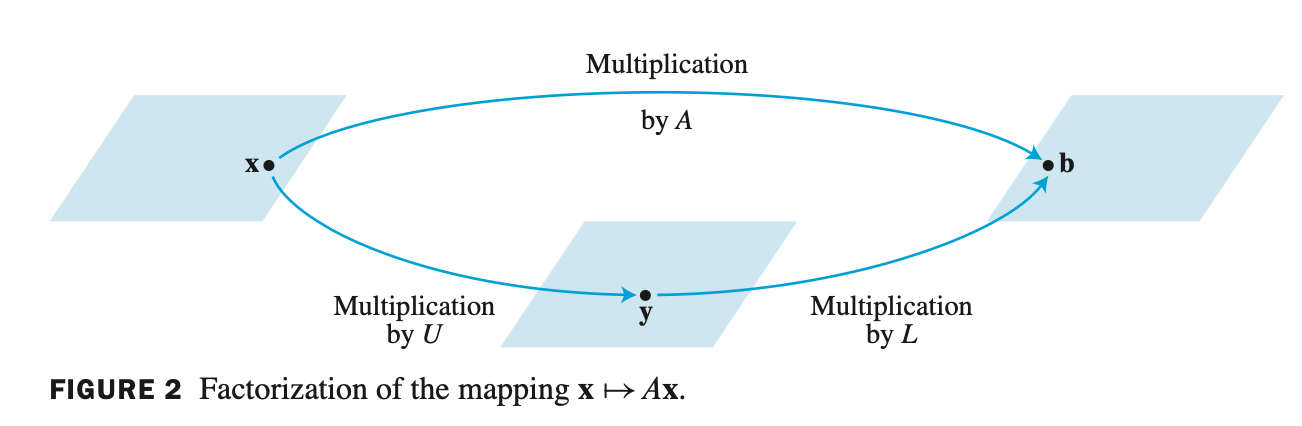
$A = LU$ 로 분해하였을 때, $A\mathbf{x} = \mathbf{b}$ 방정식을 다음과 같이 표현할 수 있다.
$A = LU$ 이므로 $A\mathbf{x} = \mathbf{b}$ 형태에 대입하면, $LU\mathbf{x} = b$ 가 됨을 알 수 있다.
이후 $U\mathbf{x} = y$ 즉, Ux 를 y 벡터로 치환한다.
$L\mathbf{y} = \mathbf{b}$ 를 통해 y 를 구하고
$U\mathbf{x} = \mathbf{y}$ 를 통해서 U와 y를 알고있으므로 최종적으로 x를 구할 수 있다.
L과 U는 pivot을 사용해서 나머지 entry 를 0으로 만들 수 있는 쉬운 형태로 이루어져 있기 때문에 빠르게 문제를 풀 수 있다.

LU decomposition 예제

위 처럼 A와 b가 주어졌을 때, 우선 $Ly = b$를 구한다.

$Ux = y$ 에서 U와 y를 알고 있으므로 x를 구할 수 있다.

이처럼 L과 U를 알고있으면 해를 구하기 쉽다.

LU Factorization Algorithm

Reduce $A$ to an echelon form $U$ by a sequence of row replacement operations, if possible.
Place entries in $L$ such that the same sequence of row operations reduces $L$ to $I$ .

A가 row replacemnt 만을 사용해서 echelon form 형태로 변환될 수 있다고 가정하자.
그러면 **U (echelon form)로 변환하기 위한 row operation elementary matrix ** $E_1, \dots, E_p$ 가 존재한다.
이 elementary matrix 의 역행렬(inverse)이 L 이 된다.
A가 $m \times n$ 행렬일 때, L과 U의 크기는 각각 $m \times m$, $m \times n$ 이 되어야한다.

\[E_p \dots E_1A = U\] \[A = (E_p \dots E_1)^{-1}U = LU\] \[L = (E_p \dots E_1)^{-1}\]

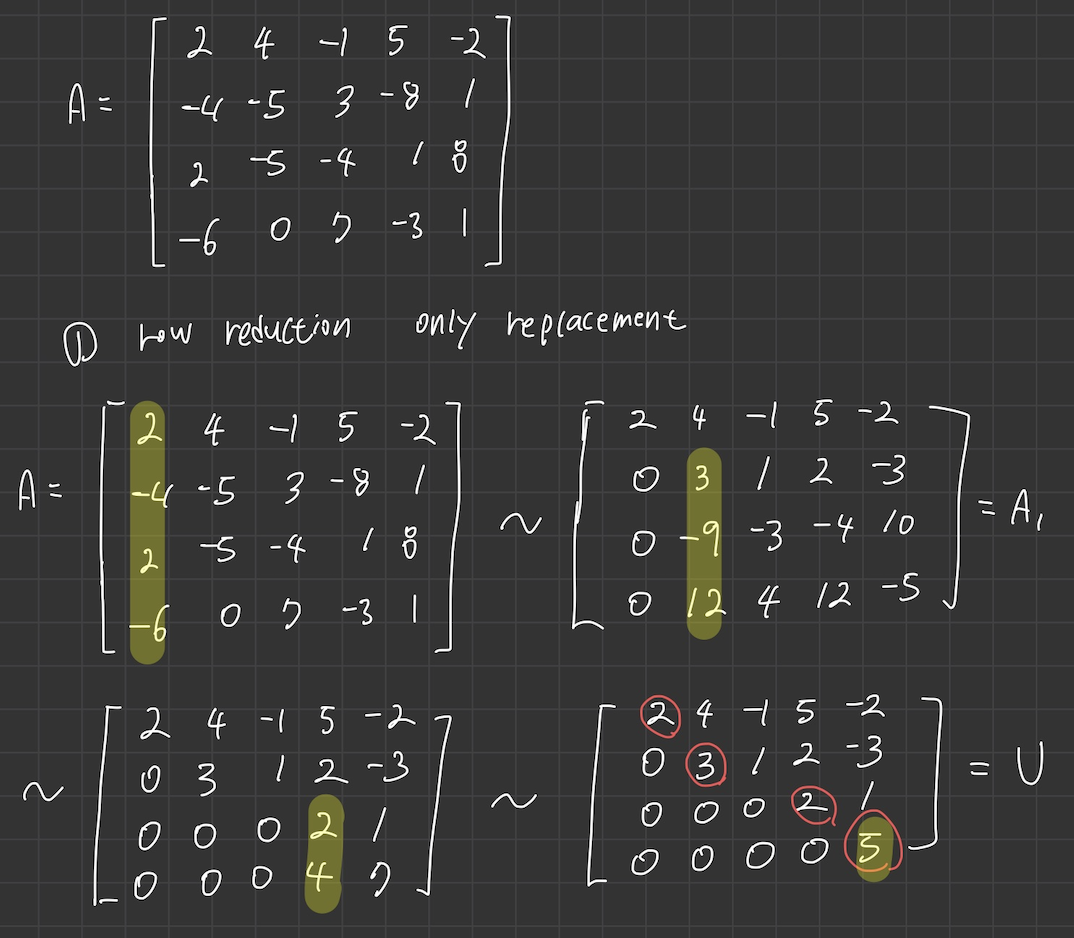
예제 풀어보기
A 가 4개의 row 를 가지고 있으므로 L은 4x4 행렬이 되어야 한다.
우선 A를 replacement 만을 사용하여 row reduction 을 해준다.

각 column 들의 pivot position 을 체크하고 그 pivot 을 기준으로 연산하기 전의 column 의 entry들을 모조리 L로 조합해준다.
여기서 주의할점은 3번째 column은 신경쓰지 않는다.

이후 조합한 행렬에서 pivot 을 나눠주고 diagonal entry 들을 모두 1로 맞춰준다.
여기서 주의할점은 -1 인 경우 해당 entry 를 갖고있는 column 에 -1을 곱해줘서 1로 만들어줘야한다.

추가 예제 풀어보기
A 가 5개의 row 를 가지고 있으므로 L은 5x5 행렬이 되어야 한다.
위 예제와 똑같이 echelon form 으로 만들기 위해 row operation 을 진행시켜준다.

L 은 5x5가 되어야하는데, pivot position은 3개밖에 안나왔다..
이럴 경우 L의 diagonal entry 는 1이 되어야 하므로 나머지 두개의 column 은 임의로 diagonal entry 가 1이 되도록 설정해주면 된다.

General Case - $ PA = LU $

echelon form 을 만들 때 interchange 가 필요한 경우 general case 형태로 문제를 풀면 된다.
여기서 P matrix 는 permutation matrix (치환 행렬)으로 Identity Matrix 로부터 얻을 수 있다. 즉, 가장 초기의 형태는 Identity Martix.
여기서는 A 행렬을 의도된 다른 순서로 뒤섞는 연산 행렬로 보면 된다. interchange 를 실행한 row 를 변경해주면 된다.

diagonal entry 가 1이되어야 하므로, 1row 와 4row 를 interchange 해주고 row operation 을 진행한다.
2row 와 3row 를 다시 interchange 해주고 이어서 row operation을 진행해준다.

P를 결정하기 위해서는 interchange 를 진행한 row 들을 P에도 똑같이 적용시켜주면 된다.

Numerical Notes - 수와 관련된 메모

여기서 연산하는 matrix 는 대부분 row 와 column 이 최소 두 자리수가 넘는 matrix이다.
flops 는 (+, -, /, *) 과 같은 연산들을 의미한다.
sparse 는 대부분이 0으로 채워져있는 경우. (diagonal entry 부근을 제외하고)

해당 메모를 간단하게 정리하자면

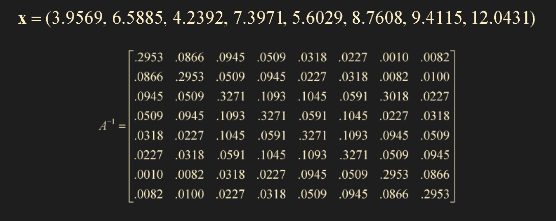
5번의 예시로는 아래 그림과 같다.

A 행렬은 sparse 하면 L과 U도 sparse 하다.

하지만, $A^{-1}$ 는 아래 그림과 같이 dense(값이 많은 경우)한 경우가 많다.

정리하자면, L과 U를 저장하는 memory 와 $A^{-1}$ 값을 저장하는 memory의 차이가 큰 것을 의미한다. 행렬의 요소들이 dense 하다면 그만큼 메모리 사용량이 증가한다는 것.
따라서, 공학적인 문제를 풀 때 LU 분해는 속도와 메모리적 측면에서 큰 이점 을 가져갈 수 있다.